中学数学|正負の数の加減算を解いてみよう

3つ以上の数の加減算
次のような3つの数の加減算を考えます。2数のときと同じ要領で解きましょう。
問
次の計算をせよ。
\begin{align*} 1. \quad \left(+2 \right)+\left(-5 \right)-\left(-4 \right) \\[ 7pt ] 2. \quad \left(-5 \right)-\left(+7 \right)-\left(-6 \right) \end{align*}2数の加減算と同じように、加算に統一することから始めます。例題と異なる手順が出てくるのは統一後です。
解答・解説では、計算過程に同色の下線を引いておきました。下線が引かれた箇所に注目しながら、計算過程をよく観察しましょう。
下線を引くことは、対応関係や変化の前後などを可視化できます。下線の色を変えると、もっと活用できるでしょう。
ただし、試験の答案に下線を引くと減点対象になるおそれがあるので、教科書やノートなどに引くようにしましょう。
問1の解答・解説
問1
次の計算をせよ。
\begin{align*} \quad \left(+2 \right)+\left(-5 \right)-\left(-4 \right) \end{align*}3つ以上の数の加減算では、正の数または負の数が2つ以上あります。問1では、負の数が2つあることが分かります。
ただし、今のままでは減算が混ざっているので、加算に統一します。
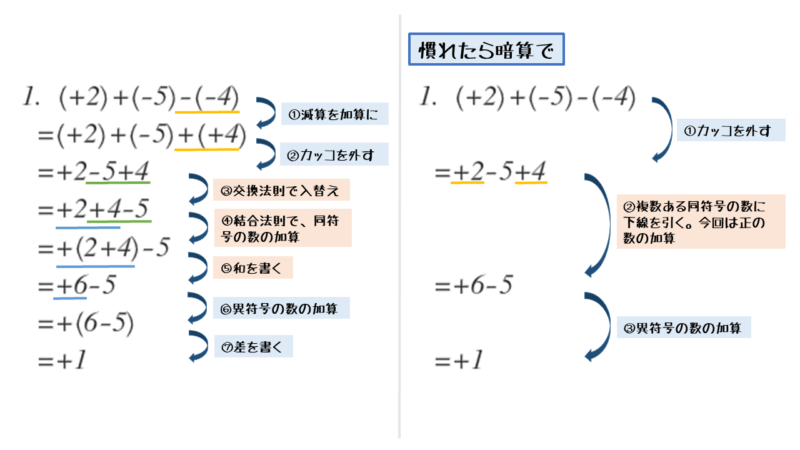
問1の解答例 1⃣
\begin{align*} \quad &\left(+2 \right)+\left(-5 \right)\underline{-\left(-4 \right)} \\[ 7pt ] = \ &\left(+2 \right)+\left(-5 \right)+\left(+4 \right) \end{align*}計算過程を書いていくとき、変化した箇所だけを書き換えていくのが計算ミスを減らすコツです。計算過程を下に記述していくので、移り変わりを確認しやすいはずです。
加算に統一すると、正の数が2つになりました。このように加算への置き換えの前後で、正負の数の個数が変化することがあるので気を付けましょう。
加算に統一できたら、加算の計算記号と数に付いたカッコを省略します。
問1の解答例 2⃣
\begin{align*} \quad &\left(+2 \right)+\left(-5 \right)\underline{-\left(-4 \right)} \\[ 7pt ] = \ &\left(+2 \right)+\left(-5 \right)+\left(+4 \right) \\[ 7pt ] = \ &+2-5+4 \end{align*}次に、左から順に加算を~といきたいところですが、交換法則や結合法則を利用して要領よく計算していきます。
交換法則や結合法則を利用して、同符号の数を優先して加算します。ここが2数の加減算と異なるところです。同符号の数だけを優先して加算するのは、異符号のときよりも計算しやすいからです。
問1の解答例 3⃣
\begin{align*} \quad &\left(+2 \right)+\left(-5 \right)\underline{-\left(-4 \right)} \\[ 7pt ] = \ &\left(+2 \right)+\left(-5 \right)+\left(+4 \right) \\[ 7pt ] = \ &+2-5+4 \\[ 7pt ] = \ &+2\underline{+4-5} \ \scriptsize{\text{(交換法則)}} \\[ 7pt ] = \ &\underline{+(2+4)}-5 \ \scriptsize{\text{(結合法則)}} \\[ 7pt ] = \ &+6-5 \end{align*}このように、同符号の数だけで加算していくと、最後には必ず異符号の2数の加算が残ります。
異符号の2数を加算します。符号と絶対値を分けて計算します。
問1の解答例 4⃣
\begin{align*} \quad &\left(+2 \right)+\left(-5 \right)\underline{-\left(-4 \right)} \\[ 7pt ] = \ &\left(+2 \right)+\left(-5 \right)+\left(+4 \right) \\[ 7pt ] = \ &+2-5+4 \\[ 7pt ] = \ &+2\underline{+4-5} \ \scriptsize{\text{(交換法則)}} \\[ 7pt ] = \ &\underline{+(2+4)}-5 \ \scriptsize{\text{(結合法則)}} \\[ 7pt ] = \ &+6-5 \\[ 7pt ] = \ &+(6-5) \ \scriptsize{\text{(異符号の $2$ 数の加算)}} \\[ 7pt ] = \ &+1 \end{align*}「同符号の数の加算から異符号の数の加算」の流れをマスターしよう。
問1のポイントと解答例をまとめると以下のようになります。
計算ミスをしないためにも、その時々の気分で解くのではなく、決まったパターンにはめて解きましょう。
問2の解答・解説
問2
次の計算をせよ。
\begin{align*} \quad \left(-5 \right)-\left(+7 \right)-\left(-6 \right) \end{align*}問2も同じ手順で解いていきます。
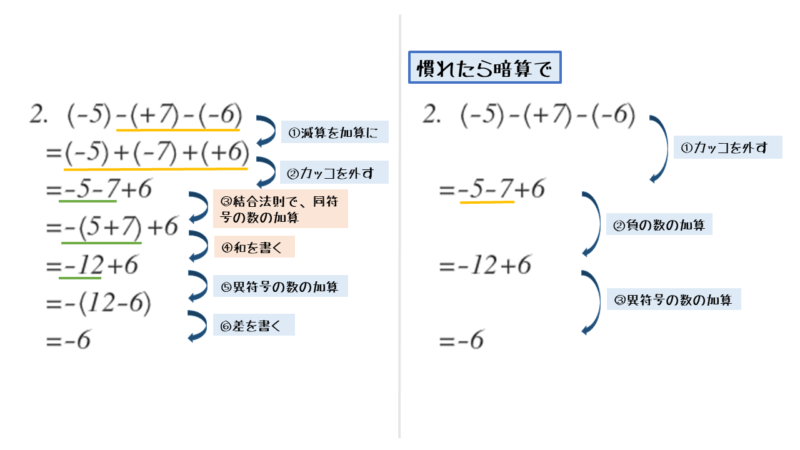
問2の解答例 1⃣
\begin{align*} \quad &\left(-5 \right)\underline{-\left(+7 \right)-\left(-6 \right)} \\[ 7pt ] = \ &\left(-5 \right)+\left(-7 \right)+\left(+6 \right) \end{align*}加算に置き換えると、2番目の数が負の数、3番目の数が正の数に変わります。
加算に統一できたら、加算の計算記号と数に付いたカッコを省略します。
問2の解答例 2⃣
\begin{align*} \quad &\left(-5 \right)\underline{-\left(+7 \right)-\left(-6 \right)} \\[ 7pt ] = \ &\left(-5 \right)+\left(-7 \right)+\left(+6 \right) \\[ 7pt ] = \ &-5-7+6 \end{align*}交換法則や結合法則を利用して、同符号の数を優先して加算します。
問2の解答例 3⃣
\begin{align*} \quad &\left(-5 \right)\underline{-\left(+7 \right)-\left(-6 \right)} \\[ 7pt ] = \ &\left(-5 \right)+\left(-7 \right)+\left(+6 \right) \\[ 7pt ] = \ &-5-7+6 \\[ 7pt ] = \ &\underline{-(5+7)}+6 \ \scriptsize{\text{(結合法則)}} \\[ 7pt ] = \ &-12+6 \end{align*}問1と同じく異符号の2数の加算が残ります。
異符号の2数を加算します。符号と絶対値を分けて計算します。
問2の解答例 4⃣
\begin{align*} \quad &\left(-5 \right)\underline{-\left(+7 \right)-\left(-6 \right)} \\[ 7pt ] = \ &\left(-5 \right)+\left(-7 \right)+\left(+6 \right) \\[ 7pt ] = \ &-5-7+6 \\[ 7pt ] = \ &\underline{-(5+7)}+6 \ \scriptsize{\text{(結合法則)}} \\[ 7pt ] = \ &-12+6 \\[ 7pt ] = \ &-(12-6) \ \scriptsize{\text{(異符号の $2$ 数の加算)}} \\[ 7pt ] = \ &-6 \end{align*}問2のポイントと解答例をまとめると以下のようになります。
まずは模範解答通りに解く習慣を。省略するのはいつでもできる。
最初は丁寧な記述を心掛けよう
解答・解説のところでポイントと解答例を紹介していますが、「慣れたら暗算で」という解き方も載せています。
「慣れたら暗算で」の方は最低限の記述になっていて、見直しのときでも問題ないでしょう。ただし、こちらから先に手をつけないように注意しましょう。あくまでも最終目標の記述例くらいにしておくのが妥当です。
簡素な記述例だと記述しないことに慣れてしまう可能性があります。これに慣れてしまうと、記述形式の試験に支障が出るかもしれません。答案を丁寧に記述した経験が自分にないからです。
最初のうちは手間を省くことを優先しないで、記述対策のために丁寧に計算過程を書くことをお勧めします。
省略するのはいつでもできます。流れを把握するために、一通り記述できるようにしておきましょう。それができるようになったら、洗練させていく方向性で取り組みましょう。
一通り過程を記述できるようになってから省略。省略するのはいつでもできる。
過程に重点を置いた学習に取り組もう
最初からステップを数段飛ばした解き方を覚えてしまうと、その間にどんな手順があったのかを覚えることができません。
数学に限らず高校での学習の目標は、答えに至るまでの過程をしっかり理解することで、答えを出すことではありません。
方針や過程が正しければ、きちんと正解を導くことができます。論理的な思考を鍛えることを意識しましょう。
中学ではもともとステップが少ないので何とかなります。しかし、高校ではそうではありません。
定義や公式などを覚えるのは当たり前で、そこからさらに踏み込んで過程に重点を置いた学習が必要になります。この学習を疎かにすると、過程を省略できない記述形式の試験では苦労するでしょう。
過程に重点を置いた学習とは、答えの根拠(因果関係)を考える学習です。言い換えると「なぜ?」「どうやって?」などと自問自答する学習のことです。丁寧な記述を勧めたのも過程に重点を置くためです。
結論だけを求める学習は中学まででおしまいにしましょう。
結論だけでなく、過程も意識した学習スタイルを確立しよう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 加減算は加算に統一。
- 加算に統一した後、同符号の数だけを優先して加算。
- 同符号の数を加算した後、最後に異符号の2数を加算。
- 計算過程の省略は流れが頭に入ってから。まずは模範解答通りに記述してみよう。
- 結論だけでなく過程にも意識した学習を心掛ける。