集合と論理|共通部分・和集合・補集合について

共通部分や和集合を扱った問題を解いてみよう
次の問題を考えてみましょう。全体集合Uの要素の数が少なく、部分集合A,Bの要素も書き並べてあります。ですから、非常に易しい部類の問題です。
まずは用語の定義など基本的な事項が頭に入っているかを意識しながら解きましょう。
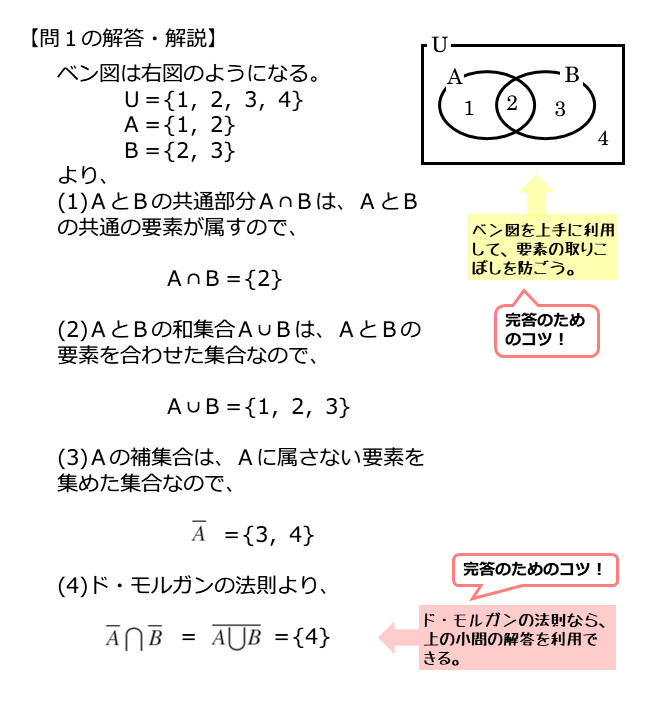
問1(1)の解答・解説
問1(1)
全体集合 $U=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}$ の $2$ つの部分集合 $A=\{1 \ , \ 2 \} \ , \ B=\{2 \ , \ 3 \}$ について、次の集合を求めよ。
\begin{align*} \quad A \cap B \end{align*}問1(1)は、部分集合A,Bの共通部分A∩Bを求める問題です。部分集合A,Bに共通の要素を探します。共通の要素は2だけです。
問1(1)の解答例
\begin{align*} &\quad A=\{1 \ , \ 2 \} \\[ 7pt ] &\quad B=\{2 \ , \ 3 \} \end{align*}より
\begin{align*} \quad A \cap B =\{2 \} \end{align*}問1(2)の解答・解説
問1(2)
全体集合 $U=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}$ の $2$ つの部分集合 $A=\{1 \ , \ 2 \} \ , \ B=\{2 \ , \ 3 \}$ について、次の集合を求めよ。
\begin{align*} \quad A \cup B \end{align*}第1問(2)は、部分集合A,Bの和集合A∪Bを求める問題です。部分集合A,Bの要素を単純に合わせるだけでは和集合にはなりません。重なった共通部分A∩Bの要素を除くことを忘れないようにしましょう。
問1(2)の解答例
\begin{align*} &\quad A=\{1 \ , \ 2 \} \\[ 7pt ] &\quad B=\{2 \ , \ 3 \} \end{align*}より
\begin{align*} \quad A \cup B &= A+B-A \cap B \\[ 7pt ] &=\{1 \ , \ 2 \}+\{2 \ , \ 3 \}-\{2 \} \\[ 7pt ] &=\{1 \ , \ 2 \ , \ 3 \} \\[ 7pt ] \therefore \ A \cup B &=\{1 \ , \ 2 \ , \ 3 \} \end{align*}問1(3)の解答・解説
問1(3)
全体集合 $U=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}$ の $2$ つの部分集合 $A=\{1 \ , \ 2 \} \ , \ B=\{2 \ , \ 3 \}$ について、次の集合を求めよ。
\begin{align*} \quad \overline{A} \end{align*}第1問(3)は、部分集合Aの補集合 $\overline{A}$ を求める問題です。全体集合Uから部分集合Aを除いた残りが補集合に属する要素です。
問1(3)の解答例
\begin{align*} &\quad U=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \} \\[ 7pt ] &\quad A=\{1 \ , \ 2 \} \end{align*}より
\begin{align*} \quad \overline{A} &= U-A \\[ 7pt ] &=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}-\{1 \ , \ 2 \} \\[ 7pt ] &=\{3 \ , \ 4 \} \\[ 7pt ] \therefore \ \overline{A} &=\{3 \ , \ 4 \} \end{align*}問1(4)の解答・解説
問1(4)
全体集合 $U=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}$ の $2$ つの部分集合 $A=\{1 \ , \ 2 \} \ , \ B=\{2 \ , \ 3 \}$ について、次の集合を求めよ。
\begin{align*} \quad \overline{A} \cap \overline{B} \end{align*}第1問(4)は、2つの補集合 $\overline{A} \ , \ \overline{B}$ の共通部分 $\overline{A} \cap \overline{B}$ を求める問題です。
2つの補集合の要素を明らかにしてから共通部分を求めても良いですが、ここではド・モルガンの法則を利用して求めます。
問1(4)の解答例 1⃣
ド・モルガンの法則より
\begin{align*} \quad \overline{A} \cap \overline{B} = \overline{A \cup B} \end{align*}ド・モルガンの法則を使って変形すると、和集合A∪Bの補集合を考えれば良いことが分かります。和集合A∪Bの要素は問1(2)で分かっているので、それを利用します。
和集合A∪Bの補集合 $\overline{A \cup B}$ は、全体集合Uから和集合A∪Bを除いた部分になります。
問1(4)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}ここで $(2)$ より
\begin{align*} \quad A \cup B =\{1 \ , \ 2 \ , \ 3 \} \end{align*}であるので
\begin{align*} \quad \overline{A \cup B} &= U-(A \cup B) \\[ 7pt ] &=\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \}-\{1 \ , \ 2 \ , \ 3 \} \\[ 7pt ] &=\{4 \} \\[ 7pt ] \therefore \ \overline{A} \cap \overline{B} &=\{4 \} \end{align*}このようにド・モルガンの法則を上手に利用すると、それまでに求めた結果を利用でき、かなり負担が減ります。
問1のポイントと解答例をまとめると以下のようになります。ベン図を利用すると、要素の書き洩らしをなくせます。
次の問題を考えてみましょう。
問2では、要素がアルファベットになっていますが、用語の定義は変わらないので、同じ要領で解いていきます。見た目が変わっても慌てないようにしましょう。
問2(1),(2)の解答・解説
問2(1),(2)
全体集合 $U=\{ a \ , \ b \ , \ c \ , \ d \}$ の $2$ つの部分集合 $A=\{a \ , \ b \ , \ c \} \ , \ B=\{b \ , \ c \ , \ d \}$ について、次の集合を求めよ。
\begin{align*} &(1) \quad A \cup B \\[ 7pt ] &(2) \quad A \cap B \end{align*}問2(1)は、部分集合A,Bの和集合A∪Bを求める問題です。和集合を求めるには共通部分が必要です。ですから、問2(2)の共通部分A∩Bを先に求めておくと良いでしょう。
共通部分A∩Bの要素は、部分集合A,Bに共通の要素です。部分集合A,Bの要素で共通のものは2つあります。共通部分の要素が分かったら、和集合の要素を求めます。
問2(1),(2)の解答例
\begin{align*} &\quad A=\{a \ , \ b \ , \ c \} \\[ 5pt ] &\quad B=\{b \ , \ c \ , \ d \} \end{align*}より
\begin{align*} \quad A \cap B = \{b \ , \ c \} \end{align*}よって
\begin{align*} \quad A \cup B &= A+B-(A \cap B) \\[ 7pt ] &=\{a \ , \ b \ , \ c \}+\{b \ , \ c \ , \ d \}-\{b \ , \ c \} \\[ 7pt ] &=\{a \ , \ b \ , \ c \ , \ d \} \quad (=U) \end{align*}和集合A∪Bは全体集合Uに等しいことが分かります。
問2(3)の解答・解説
問2(3)
全体集合 $U=\{ a \ , \ b \ , \ c \ , \ d \}$ の $2$ つの部分集合 $A=\{a \ , \ b \ , \ c \} \ , \ B=\{b \ , \ c \ , \ d \}$ について、次の集合を求めよ。
\begin{align*} \quad \overline{B} \end{align*}問2(3)は、部分集合Bの補集合 $\overline{B}$ を求める問題です。全体集合Uから部分集合Bを除いた残りが補集合に属する要素です。
問2(3)の解答例
\begin{align*} &\quad U=\{ a \ , \ b \ , \ c \ , \ d \} \\[ 5pt ] &\quad B=\{b \ , \ c \ , \ d \} \end{align*}より
\begin{align*} \quad \overline{B} &= U-B \\[ 7pt ] &=\{ a \ , \ b \ , \ c \ , \ d \}-\{b \ , \ c \ , \ d \} \\[ 7pt ] &=\{a \} \\[ 7pt ] \therefore \ \overline{B} &=\{a \} \end{align*}問2(4)の解答・解説
問2(4)
全体集合 $U=\{ a \ , \ b \ , \ c \ , \ d \}$ の $2$ つの部分集合 $A=\{a \ , \ b \ , \ c \} \ , \ B=\{b \ , \ c \ , \ d \}$ について、次の集合を求めよ。
\begin{align*} \quad \overline{A} \cup \overline{B} \end{align*}問2(4)は、2つの補集合 $\overline{A} \ , \ \overline{B}$ の和集合 $\overline{A} \cup \overline{B}$ を求める問題です。
問2(3)で部分集合Bの補集合を求めたので、部分集合Aの補集合を求めれば解けます。ここでは、問1(4)と同じようにド・モルガンの法則を利用して与式を変形します。
問2(4)の解答例 1⃣
ド・モルガンの法則より
\begin{align*} \quad \overline{A} \cup \overline{B} = \overline{A \cap B} \end{align*}ド・モルガンの法則から、共通部分A∩Bの補集合を考えれば良いことが分かります。共通部分A∩Bの要素は問2(2)で求めたので、それを利用します。
共通部分A∩Bの補集合 $\overline{A \cap B}$ は、全体集合Uから共通部分A∩Bを除いた部分です。
問2(4)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}ここで $(2)$ より
\begin{align*} \quad A \cap B =\{b \ , \ c \} \end{align*}であるので
\begin{align*} \quad \overline{A \cap B} &= U-(A \cap B) \\[ 7pt ] &=\{ a \ , \ b \ , \ c \ , \ d \}-\{b \ , \ c \} \\[ 7pt ] &=\{a \ , \ d \} \\[ 7pt ] \therefore \ \overline{A} \cup \overline{B} &=\{a \ , \ d \} \end{align*}問2のポイントと解答例をまとめると以下のようになります。解答例のようにベン図を描いて解きましょう。
集合を扱うとき、ベン図はとても役立ちます。集合が3つ以上になったり、要素の個数が増えたりすると描くのが意外と難しくなります。描き慣れておきましょう。
Recommended books
メタ認知のためにも演習をこなすことは大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
特に、思考力を問われる問題の比重が過去に比べて増えてきています。パターンの暗記だけでは対応できなくなってきています。
オススメその1
そこで紹介するのが河合塾シリーズの『これからの大学入試に必要な数学の「思考力」を鍛える問題集』です。
河合塾数学科の考える「思考力・判断力・表現力」をまとめ、これに基づいて過去の入試問題を分析し、その中から思考力を養うために経験しておきたい問題を収集し解答・解説を収録。また、思考調査の問題を参考にして「共通テスト型問題」を作成。
センター試験から共通テストへと変わったことにより、「思考力・判断力・表現力」を問う問題が今まで以上に出題されると考えられます。これらは短期間で習得するのはなかなか難しいものです。日頃から訓練して身に付けるものなので、このような教材を利用してできるだけ早く取り組みたいところです。
オススメその2
バカロレア試験は、フランスの大学入学資格試験です。論述試験が中心です。思考力はもとより表現力も必要な試験です。
思考力・表現力を保障するには、大学教育の準備学力として、大学入試でどのような思考力・表現力を問うべきか。思考力・表現力を評価する論述型大学入試の実現に何が必要か。この思考力・表現力を中学校、高校でいかに育むべきか。本書では、論述試験中心のフランスの大学入学資格試験・バカロレア試験の問題や模範解答、採点規準、フランスの学校での授業観察などをもとに、これらの問いへのヒントを示す。第一人者が結集して執筆した、バカロレア研究の最前線。
海外に留学したいと考えている人にはおすすめです。思考力や表現力を短期間で養成するのは簡単ではありません。ですから、出来るだけ早く、意識的に取り組んでおいた方が良いでしょう。
さいごに、もう一度、頭の中を整理しよう
- ベン図で可視化して、集合の関係を理解する。
- 共通部分・和集合・補集合の記号をしっかり使えるようにする。
- 集合や要素の書き方を工夫する。
- 補集合を扱うとき「ド・モルガンの法則」を念頭に。