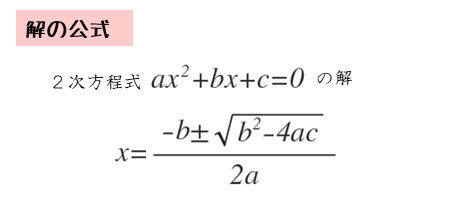2次関数|2次方程式の解の判別について

2次方程式の解法について学習したので、今回は、2次方程式の解の判別について学習しましょう。
解の判別ができれば、「2次方程式からどんな解が得られるのか」を知ることができます。
2次方程式の解を判別できる式
2次方程式の解法を学習したので、解を求めることはできるようになりました。
しかし、高校数学では、実数以外の数を扱うことがあります。そのような場合、これまでの知識ではどんなに頑張っても2次方程式を解くことができません。
ですから、解が実数であるかどうかや、得られる解の個数などを方程式を解く前に知ることは意外と大切なことです。
解が実数なのかそうでないのか、また、解は何個得られるのか、といった情報を事前に知る方法があります。それが解の判別です。
解を判別できれば、たとえば解が実数で得られないと事前に知ることができます。解が実数でなければ、2次方程式を解くことはできません(今の段階では)。解けない方程式を一生懸命解こうとする、という無駄なことをしなくて済むようになります。
解の公式に注目する
2次方程式の解の公式は以下のように表されます。
これまで扱ってきた数は、実数の範囲にある数です。
一般に、2次方程式の解もこれまでと同様に実数で得られることが多いです。ちなみに、実数である解のことを実数解と言います。
2乗に比例する関数とは、中学で学習する関数のこと。高校数学では、2次関数に含まれる。
先ほど、2次方程式の解は実数解で得られることが多いと言いました。あくまでも多いと言うだけで確実に実数解であるわけではありません。ですから、場合によっては実数解が得られないこともあります。
今のところ実数解が得られない場合、2次方程式を解くことができないので死活問題になります。ですから、2次方程式の解が実数解であるかどうかを事前に知ることは重要です。
2次方程式の解が実数解になるかどうかの条件は、解の公式から得られます。
解の公式から得られる条件
条件が2次方程式の解の公式から得られることは分かりました。具体的には、根号の中にある式b2-4acの値によって条件が得られます。
b2-4acを含む部分は平方根です。平方根も実数の範囲にある数です。ここで、平方根について今回の話に関わる大事な性質を確認しておきます。
たとえば、-3の平方根を考えてみましょう。2乗して-3になる数が-3の平方根です。そのような数が実数の範囲に存在するでしょうか?
負の数の平方根は実数の範囲に存在するか?
- (3の平方根)= $\pm \sqrt{3}$(2乗すると正の数3になる数が3の平方根)
- (-3の平方根)= $\pm \sqrt{-3}$(2乗すると負の数-3になる数が-3の平方根)
-3の平方根は2乗すると負の数-3になる数ですが、2乗して負の数になるものは実数の範囲には存在しません。ですから、平方根には「負の数の平方根は存在しない」という性質があります。
実数の性質と負の平方根
- 実数の範囲では、2乗すると必ず0以上の数になる。(参考:数と式|数の定義について)
- 負の数の平方根は存在しないが、負の平方根($\pm \sqrt{-3}$)は存在する。(参考:数と式|平方根について)
このような性質をもつ平方根が解の公式にも存在します。この平方根が実数として存在するかどうかは、根号の中にある式b2-4acの値を調べることで分かります。
このように、平方根の性質を利用することで、2次方程式の解が実数解であるかどうかを判別できるわけです。
実数解の判別は、平方根が実数として存在するかどうか、つまりb2-4acの値を調べること。2乗に比例する関数とは、中学で学習する関数のこと。高校数学では2次関数に含まれる。
根号の中にある式b2-4acは2次方程式の解を判別することができる式と言う意味で判別式と呼ばれます。
一般に、判別式b2-4acは、代わりに文字Dで表されることもあります。2次方程式の解に注目する際、解の判別式がよく使われます。ですから、文字Dを使って簡略化できると記述もラクになります。
2次方程式の解の判別式
$2$ 次方程式
\begin{align*} \quad ax^{2}+bx+c=0 \end{align*}の解は、解の公式より
\begin{align*} \quad x = \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \end{align*}ここで
\begin{align*} \quad D = {b}^{2}-4ac \end{align*}とおくと
\begin{align*} \quad x &= \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \\[ 7pt ] &= \frac{-b \pm \sqrt{D}}{2a} \end{align*}2次方程式の解を判別できるから判別式と言う。便宜上、判別式を文字Dに置き換えることが多い。
単に「判別式」と言う場合が多いせいか、「何の判別ができるのか?」と聞かれて答えられない人が意外と多いです。できる限り「2次方程式の解の」と言う部分を省かないようにしましょう。
「2次方程式の解の」という文言が示すように、判別式は2次方程式に対して使われる式であって、どんな式にも使えるものではありません。
判別式は、2次方程式がなければ使うことができない。判別式を使う場合、必ず2次方程式を導出しよう。
2次方程式の解と判別式との関係
2次方程式の解が実数解であるかどうかは、2次方程式の係数a,cや定数項bの値を判別式D=b2-4acに代入し、そのときの値を調べれば分かります。
2次方程式の解とその判別式
\begin{align*} \quad D = {b}^{2}-4ac \end{align*}とおくと
\begin{align*} \quad x &= \frac{-b \pm \sqrt{{b}^{2}-4ac}}{2a} \\[ 7pt ] &= \frac{-b \pm \sqrt{D}}{2a} \end{align*}判別式D=b2-4acの値は3通り考えられます。
判別式の値は3パターン
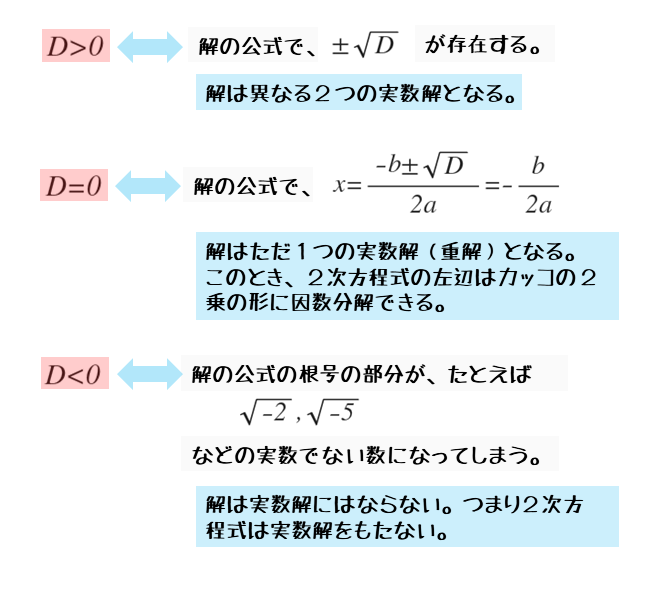
- (D>0のとき)=(D=b2-4acの値が正の数になるとき)
- (D=0のとき)=(D=b2-4acの値が0になるとき)
- (D<0のとき)=(D=b2-4acの値が負の数になるとき)
それぞれの場合で、2次方程式の解がどうなるのかを解の公式と併せて見ていきます。
D>0のとき
D>0のとき
\begin{align*} \quad x = \frac{-b \pm \sqrt{D}}{2a} \end{align*}において
\begin{align*} \quad D \gt 0 \end{align*}すなわち
\begin{align*} \quad {b}^{2}-4ac \gt 0 \end{align*}のとき
「D>0のとき」とは、言い換えると「b2-4acの値が正の数のとき」です。このとき、解の $\pm \sqrt{D}$ は正の数Dの平方根になり、実数として存在します。
ですから、D>0のとき、2次方程式の解は実数解になります。
また、$\pm \sqrt{D}$ は、正の平方根 $+\sqrt{D}$ と負の平方根 $-\sqrt{D}$ の2つをまとめて表したものなので、2次方程式の解は2つあります。
まとめると「D>0のとき、2次方程式の解は異なる2つの実数解である」ことが分かります。一般に、「D>0のとき、2次方程式は異なる2つの実数解をもつ」という言い方をします。
D=0のとき
D=0のとき
\begin{align*} \quad x = \frac{-b \pm \sqrt{D}}{2a} \end{align*}において
\begin{align*} \quad D = 0 \end{align*}すなわち
\begin{align*} \quad {b}^{2}-4ac = 0 \end{align*}のとき
\begin{align*} \quad x = \frac{-b \pm \sqrt{0}}{2a} \end{align*}よって
\begin{align*} \quad x = -\frac{b}{2a} \end{align*}「D=0のとき」とは、言い換えると「b2-4acの値が0のとき」です。このとき、$\pm \sqrt{D}=0$ となるので、解の中に平方根が存在しなくなります。
平方根が消えた後の解を見ると分かるように、解は実数です。ですから、D=0のとき、2次方程式の解は実数解になります。
また、平方根が存在しなくなったことで、2次方程式の解は-b/2aの1つだけになります。このように2次方程式の解が1つだけのとき、その解を重解と言います。
重解は、2次方程式を因数分解すると式が ${(x+b/2a)}^{2}=0$ の形になったときの解。カッコの中の式が同じであれば、解が重なる(同じになる)。重解は1つとして扱う。
まとめると「D=0のとき、2次方程式の解は1つの実数解である」ことが分かります。一般に、「D=0のとき、2次方程式は重解をもつ」という言い方をします。
D<0のとき
D<0のとき
\begin{align*} \quad x = \frac{-b \pm \sqrt{D}}{2a} \end{align*}において
\begin{align*} \quad D \lt 0 \end{align*}すなわち
\begin{align*} \quad {b}^{2}-4ac \lt 0 \end{align*}のとき
「D<0のとき」とは、言い換えると「b2-4acの値が負の数のとき」です。このとき、解の $\pm \sqrt{D}$ は負の数Dの平方根になり、実数として存在しません。
ですから、D<0のとき、2次方程式の解は実数解ではないことが分かります。ここでは実数の範囲を扱っているので、2次方程式の解は0個です。
まとめると「D<0のとき、2次方程式の解は実数解ではない」ことが分かります。一般に、「D<0のとき、2次方程式は実数解をもたない」という言い方をします。
複素数の単元で、虚数について学習します。負の数の平方根は虚数であるので、「2次方程式は虚数解をもつ」という言い方をします。
以上のように、判別式の値によって2次方程式の解が決まることが分かります。別の言い方をすれば、2次方程式の解は、係数や定数項によって決まるとも言えます。
判別式を上手に利用できれば、実数解をもつのか、もつとすれば何個もつのか、などを事前に知ることができます。そうすると、計算ミスに気付くこともできます。
次は2次方程式の解の判別式を扱った問題を実際に解いてみましょう。