２次関数｜２次方程式の解の判別について

04/07/2022数学１

判別式を扱った問題を解いてみよう

判別式を扱った問題では、解の判別に始まり、実数解の個数を調べたり、係数や定数項を求めたり、など多岐にわたります。

まずは基本となる解の判別や実数解の個数に関する問題を解けるようになりましょう。

解を判別してみよう

次の問題を解いてみましょう。判別式の入門レベルです。

問１の解答・解説

２次方程式の解を判別する問題です。係数や定数項をＤ＝ｂ²－４ａｃの右辺に代入し、Ｄの値を求めます。

問１

次の２次方程式の解を判別せよ。

\begin{align*} 1. \quad 3x^{2}+2x-1=0 \end{align*}

与式と判別式の対応関係を把握して、対応する値を判別式に代入します。

問１の解答例

\begin{align*} \quad 3x^{2}+2x-1=0 \end{align*}

与式の判別式を $D$ とおくと

\begin{align*} \quad D &=2^{2}-4 \cdot 3 \cdot \left( -1 \right) \\[ 7pt ] &=4+12 \\[ 7pt ] &=16 \gt 0 \end{align*}

$D \gt 0$ より、与式は異なる $2$ つの実数解をもつ。

一般に、判別式と言えば文字Ｄを使いますが、「判別式をＤとすると」などと一言断ってからにしましょう。

判別式Ｄの値が正の数になったのでＤ＞０です。このことから、２次方程式は異なる２つの実数解をもつと言えます。

問１のポイントと解答例をまとめると以下のようになります。

問２の解答・解説

問２

次の２次方程式の解を判別せよ。

\begin{align*} 2. \quad 9x^{2}-12x+4=0 \end{align*}

問２も同じ要領で解きます。

問２の解答例

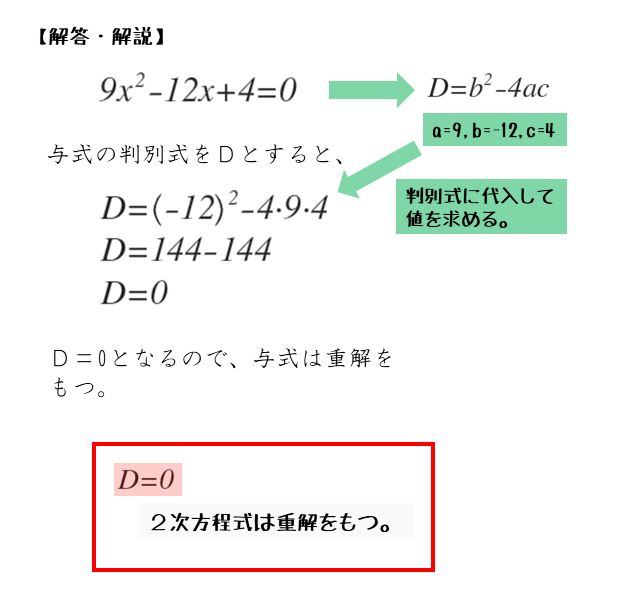
\begin{align*} \quad 9x^{2}-12x+4=0 \end{align*}

与式の判別式を $D$ とおくと

\begin{align*} \quad D &=\left( -12 \right)^{2}-4 \cdot 9 \cdot 4 \\[ 7pt ] &=144-144 \\[ 7pt ] &= 0 \end{align*}

$D = 0$ より、与式は重解をもつ。

判別式Ｄの値が０になったのでＤ＝０です。このことから、２次方程式は重解をもつと言えます。

問２のポイントと解答例をまとめると以下のようになります。

問１，２では、２次方程式から対応する数を抜き出し、四則計算ができれば解ける問題です。「判別式を使ってみよう」という意味合いが強いので、入試レベルではほとんど見かけなくなります。

解の条件から係数や定数項を決めよう

次の問題を解いてみましょう。入試でも見かけるレベルですので、ぜひ解けるようにしておきましょう。

問３の解答・解説

問３は、判別式の条件から解を判別するのではなく、解の条件から係数を決定する問題です。

解の判別ができれば、判別式の値の条件が分かります。互いに等価な条件を理解しているかどうかが問われています。

互いに等価な条件を覚えよう

（２次方程式の解）＝（係数や定数項の関係）
（異なる２つの実数解をもつ）＝（Ｄ＞０すなわちｂ²－４ａｃ＞０）
（重解をもつ）＝（Ｄ＝０すなわちｂ²－４ａｃ＝０）
（実数解をもたない）＝（Ｄ＜０すなわちｂ²－４ａｃ＜０）

２次方程式の解と判別式の値との関係を正しく理解しましょう。

これらを踏まえて、２次方程式が重解をもつときの定数ｋの値を求めます。

２次方程式が重解をもつためには、判別式ｂ²－４ａｃの値が０でなければ成り立ちません。この関係を利用すると、定数ｋについての方程式を導出できます。

問３の解答例 1⃣

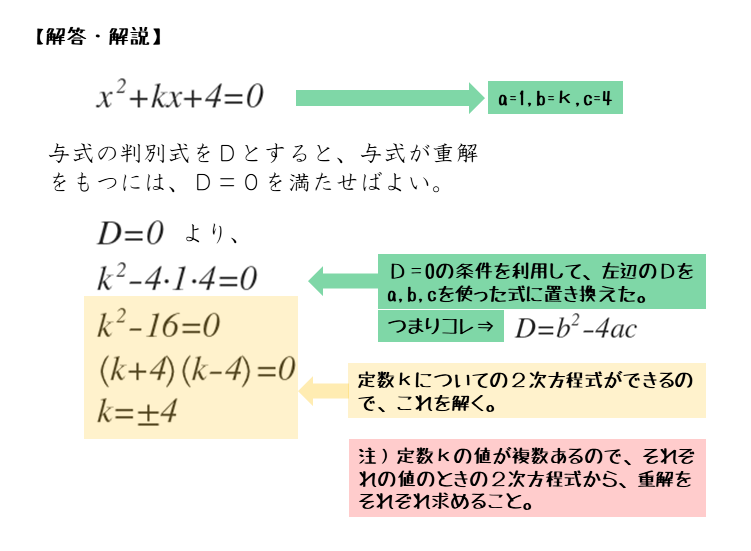
\begin{align*} \quad x^{2}+kx+4=0 \end{align*}

与式の判別式を $D$ とおくと

\begin{align*} \quad D &= k^{2}-4 \cdot 1 \cdot 4 \\[ 7pt ] &= k^{2}-16 \end{align*}

与式が重解をもつのは、$D = 0$ のときあるので

\begin{align*} \quad k^{2}-16 =0 \end{align*}

これを解くと

\begin{align*} \quad k = \pm 4 \end{align*}

定数ｋの値を求めたいので、定数ｋについての方程式を導出します。そのために、問題で指定された解の条件を利用します。

判別式ｂ²－４ａｃは、２次方程式の係数や定数項で表されます。このことが分かっていれば、定数ｋについての方程式を導出できることに気付けたかもしれません。

２次方程式の解を求めるには、係数や定数項が決まっていなければなりません。定数ｋの値が分かると、２次方程式が決まるので、解を求めることができるようになります。

問３の解答例 2⃣

\begin{align*} \quad k = \pm 4 \end{align*}

より、与式は

\begin{align*} \quad x^{2}+4x+4=0 \end{align*}

または

\begin{align*} \quad x^{2}-4x+4=0 \end{align*}

$k = 4$ のとき

\begin{align*} \quad x^{2}+4x+4 &=0 \\[ 7pt ] \left( x+2 \right)^{2} &= 0 \\[ 7pt ] \therefore x &=-2 \end{align*}

$k = -4$ のとき

\begin{align*} \quad x^{2}-4x+4 &=0 \\[ 7pt ] \left( x-2 \right)^{2} &= 0 \\[ 7pt ] \therefore x &=2 \end{align*}

よって

$k =4$ のとき、重解は $-2$

$k =-4$ のとき、重解は $2$

２次方程式の解は重解になることが分かっているので、方程式を解くと必ず重解が得られます。計算ミスがないようにしましょう。

問１，２と問３との比較

問１，２と問３とを比較してみましょう。ちょうど逆の関係になっていることが分かります。

問１，２の流れ

２次方程式が決まっている

⇒係数や定数項で表される判別式の値が決まる

⇒解の判別ができる

問３の流れ

解の判別ができる

⇒係数や定数項で表される判別式の値が決まる

⇒２次方程式の係数や定数項が決まる

応用の部類に入る問題は、問３のように逆側からアプローチする問題が多いのが特徴です。

学習する際のコツとしては、対応関係を一方向から眺めるだけでなく、逆方向からも眺めることが必要です。そのような視点を身に付けるのはなかなか難しいので、応用問題を積極的に解くと良いでしょう。

また、過程を疎かにせず、答えまでの流れを意識して学習することも大切です。

Recommended books

関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。

関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。

関数は、たとえば物理の直線運動でもｖ－ｔグラフなどで登場するので、ぜひとも攻略しておきたい単元です。

オススメその１

１冊目に紹介するのは『おもしろいほどよくわかる高校数学関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。

高校数学で学ぶ２次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。

書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。

おもしろいほどよくわかる高校数学関数編

created by Rinker

オススメその２

２冊目に紹介するのは『改訂版坂田アキラの２次関数が面白いほどわかる本』です。

『おもしろいほどよくわかる高校数学関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。

高校数学の基幹分野である「２次関数」は坂田の解説でマスターせよ！
累計５０万部超の「坂田理系シリーズ」の「２次関数」。２００９年４月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「２次関数」対策の決定版！！旧版になかった「解の配置」のテーマを増設。

教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。