数と式|一次不等式について

今回は「一次不等式」について学習します。一次不等式では不等式の性質を利用します。
一次不等式について
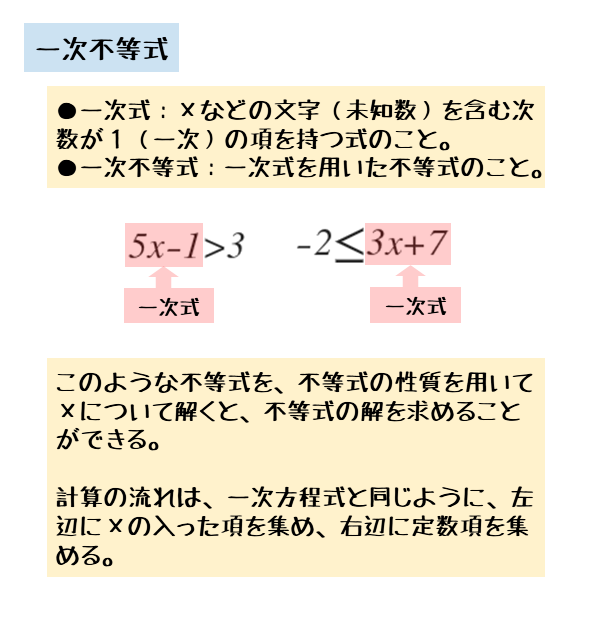
一次不等式とは、特定の文字についての一次式を用いた不等式のことです。なお、一次式とは文字を含む項の最高次数が1である式のことです。
たとえば、文字xについての一次式を挙げると以下のようになります。
一次不等式の例
\begin{align*} &\quad 5x-1 \gt 3 \\[ 7pt ] &\quad -2 \leqq 3x+7 \end{align*}このような一次不等式では、不等式の性質を用いて式変形することで、文字xの値の範囲を求めることができます。不等号を使っているので、解が文字xの値の範囲で与えられることが方程式などの解とは異なります。
不等式の解は値の範囲で与えられる。ただし、自然数の範囲で考えるなどの特定の条件があれば、解は特定の値になるときがある。
一次不等式に関わる用語
一次不等式でも専門的に使う用語が出てきます。問題文や解説などでも使われるので、出題の意図を読み取れるようにしっかり覚えましょう。
一次不等式に関わる用語
- 一次不等式の解
- 一次不等式を解く
一次不等式の解とは、文字(未知数)の取りうる値の範囲のことです。
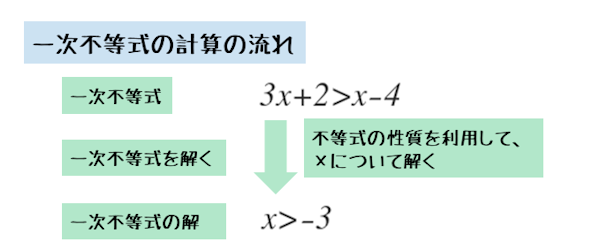
また、一次不等式を解くとは、解を求めることです。一次不等式を解くためには、不等式の性質を利用しながら式を変形します。
一次不等式を解く流れ
一次不等式を解く流れは、一次方程式と基本的に変わりません。
方程式のときと同じように、文字を含む項を左辺に集め、定数項を右辺に集めます。
一次不等式の計算の流れ
- 左辺に文字を含む項を集め、右辺に定数項を集めて整理する。
- 左辺の項の係数を見て、その逆数を乗算する。
- 右辺の乗算をすると、解が得られる。
逆数を乗算するのは、左辺にある一次の項の係数を1にするためです。
一次方程式や一次不等式では、左辺に注目しながら変形するのがコツ。
移項の仕組みをもう一度確認
方程式や不等式の解を求めるために、式変形をします。その中でもよく利用するのが移項です。
移項は「両辺に正負の数を加算しても等式や不等式が成り立つ」という性質を利用しています。
実際には両辺に同じ数を加算しているのですが、片方の辺は相殺されてしまいます。そうすると、あたかも一方の辺から他方の辺に項が移動したように見えます。このことから移項と言われます。
一次方程式や一次不等式を解くとき、両辺に数を加算するのは不要な項をなくすのが目的なので、同じ数を加算するのと同じ効果のある移項で済ませてしまいます。できるだけ記述を楽にする効果があります。
移項は、両辺に同じ数を加算した後の結果。項を移動したわけではない。移項するとき、項の符号が変わるので注意しよう。
一次不等式の解を数直線で表す
一次不等式を解くと、解が不等式で得られます。この不等式が文字(未知数)が取り得る値の範囲を表します。
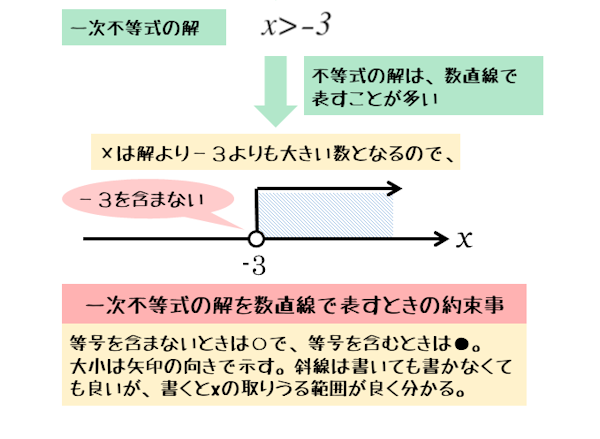
たとえば、解がx>-3であれば、-3より大きい数はすべて解になります。
このような一次不等式の解を扱う場合、解を数直線で表すと、取り得る値の範囲を可視化できるので、非常に分かりやすくなります。
不等式を図示するとき、たとえば「3以上なのか」「3より大きいのか」が分かるように図示します。
不等号が≧,≦のように等号を含むときは●(黒丸)で表し、>,<のように等号を含まないときは○(白丸)で表します。
範囲の上限値または下限値になる数が解に含まれるかどうかは重要。黒丸と白丸をきちんと区別して使おう。
一次不等式に慣れるために、一次不等式を扱った問題を実際に解いてみましょう。
一次不等式を扱った問題を解いてみよう
2問とも文字xについての一次不等式です。不等式の性質を用いて式変形し、一次不等式を解きます。
問1の解答・解説
問1
次の不等式を解け。
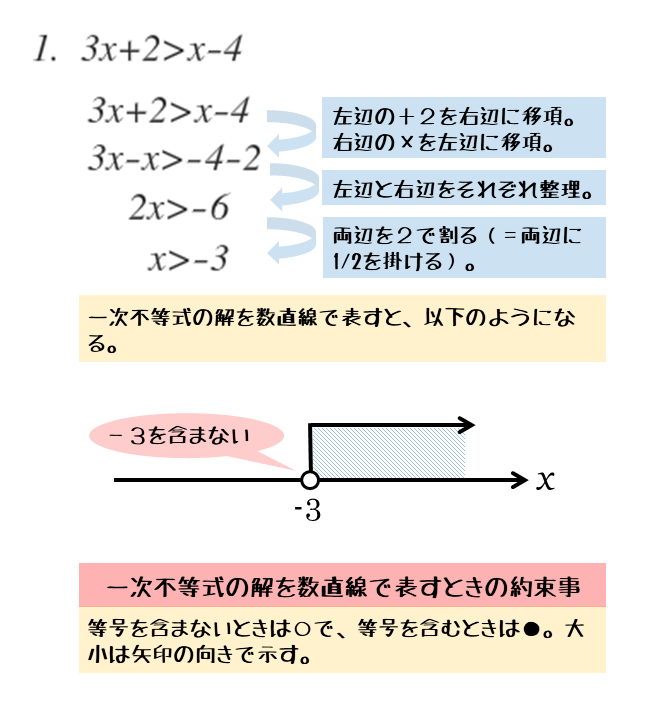
\begin{align*} \quad 3x+2 \gt x-4 \end{align*}文字xを含む項を左辺に、定数項を右辺に集めるために移項します。このとき、移項した項の符号が変わることに注意しましょう。
移項できたら、それぞれの辺を整理します。
問1の解答例 1⃣
与式を整理すると
\begin{align*} \quad 3x+2 &\gt x-4 \\[ 7pt ] \quad 3x-x &\gt -4-2 \\[ 7pt ] \quad 2x &\gt -6 \end{align*}左辺と右辺をそれぞれ整理できたら、左辺にある一次の項(xの項)の係数を1にする処理を行います。
係数を1にするには、文字xの係数2の逆数である1/2を両辺に掛けます。
もちろん、係数2で割っても良いのですが、今後のことを考えると除算よりも乗算に慣れておいた方が良いでしょう。
整理すると、一次不等式の解が得られます。
問1の解答例 2⃣
\begin{align*} \quad &\vdots \\[ 7pt ] \quad 2x &\gt -6 \\[ 7pt ] \quad 2x \times \frac{1}{2} &\gt -6 \times \frac{1}{2} \\[ 7pt ] \quad x &\gt -3 \end{align*}問1のポイントと解答例をまとめると以下のようになります。
問2の解答・解説
問2
次の不等式を解け。
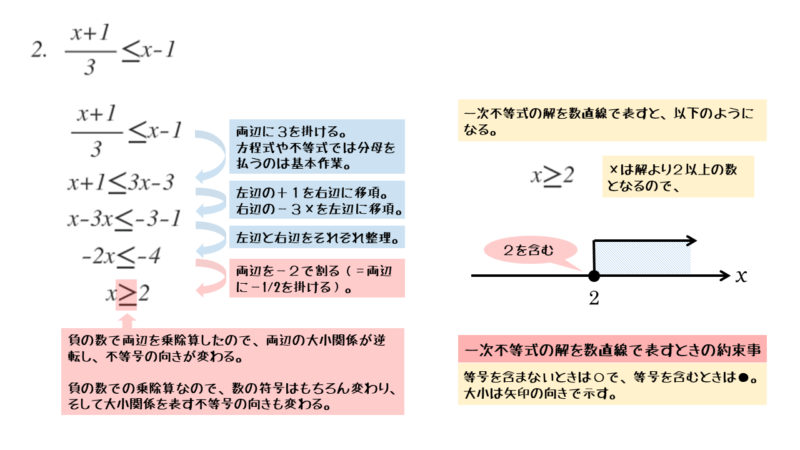
\begin{align*} \quad \frac{x+1}{3} \leqq x-1 \end{align*}与式を見ると、左辺が分数になっています。左辺や右辺に分数があれば、一次方程式と同じように整数にすることから始めましょう。
問2では、分母が3の分数があるので、両辺に3を掛けて分母を払います。分数から整数に変形できたら、問1と同じ流れで式を変形していきます。
問2の解答例 1⃣
与式を変形すると
\begin{align*} \quad \frac{x+1}{3} &\leqq x-1 \\[ 7pt ] \quad \frac{x+1}{3} \times 3 &\leqq \left(x-1 \right) \times 3 \\[ 7pt ] \quad x+1 &\leqq 3x-3 \\[ 7pt ] \quad x-3x &\leqq -3-1 \\[ 7pt ] \quad -2x &\leqq -4 \end{align*}注意したいのは、右辺に3を掛けるときです。カッコを使わずに記述すると、xやー1だけに掛けることになってしまいます。右辺全体に掛けるようにしましょう。
式全体に掛けるときはカッコを使う
$-1$ だけに $3$ を掛けた式
\begin{align*} \quad x-1 \times 3 = x-3 \end{align*}$x$ だけに $3$ を掛けた式
\begin{align*} \quad 3 \times x-1 = 3x-1 \end{align*}右辺全体に $3$ を掛けるには、多項式をカッコをくくること
\begin{align*} &\quad 3 \times \left(x-1 \right) = 3x-3 \\[ 7pt ] &\quad \left(x-1 \right) \times 3 = 3x-3 \end{align*}左辺と右辺をそれぞれ整理すると、項がそれぞれ1つだけになっているはずです。
一次方程式や一次不等式では、ax=bやax>bなどの形を目指して式を変形しよう。
さいごに左辺にある一次の項(xの項)の係数を1にする処理をして整理すると、一次不等式の解が得られます。
問2の解答例 2⃣
\begin{align*} \quad &\vdots \\[ 7pt ] \quad -2x &\leqq -4 \\[ 7pt ] \quad -2x \times \left( -\frac{1}{2} \right) &\geqq -4 \times \left( -\frac{1}{2} \right) \\[ 7pt ] \quad x &\geqq -2 \end{align*}-2の逆数となる負の数-1/2を両辺に掛けたので、不等号の向きが変わることに注意しましょう。
-2xの係数を1にする処理では、負の数ー2で両辺を割ってもよい。
問2のポイントと解答例をまとめると以下のようになります。
一次方程式と異なるのは、負の数を乗除算するとき。不等号の向きが逆向きになる。
一次不等式を解くとき、変形の流れを把握して目標の式の形へ変形していくことが大切です。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 一次不等式は、特定の文字についての一次式を用いた不等式のこと。
- 一次不等式の解は、文字(未知数)の取りうる値の範囲になる。
- 一次不等式の解を求めることを、一次不等式を解くという。
- 一次不等式の解は、数直線で表すと分かりやすい。
- 解を図示するとき、等号があれば●(黒丸)で表す。
- 解を図示するとき、等号がなければ○(白丸)で表す。
- 大小は矢印の向きで表す。