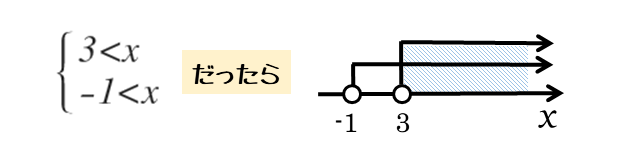数と式｜連立不等式について
今回は連立不等式について学習します。「連立～式」と言われるものに連立方程式があります。連立する式が方程式から不等式に変わっただけです。
解くときに不等式の性質を利用するので確認しながら進めていくと良いでしょう。
連立不等式について
連立不等式とは、複数の不等式を組み合わせた式のことです。
連立方程式の解との違い
２種類の文字ｘ，ｙを使った方程式を二元一次方程式と言います。中学でも扱われる方程式です。このような方程式の解は、無数に存在し、１つに定まりません。
それに対して、２つの二元一次方程式を連立すると、どちらの方程式も満たさなければならないので、このときの解はただ１つ（共通解）に定まります。
１つの方程式だけでは解が定まりませんが、複数の方程式を連立すれば、１つの解に定まります。
未知数が２つあるとき、条件式（二元一次方程式）が１つだけでは求めることができない。求めるためには、条件式を２つ作る必要がある。未知数の数だけ条件式を用意しよう。
連立不等式は、複数の不等式を連立したものです。連立不等式の解は、それぞれの不等式が満たす範囲の共通部分になります。解が値の範囲なので、特定の値だけが解に定まらないのが一般的です。
連立方程式とは異なり、連立不等式の解は文字（未知数）の取り得る値の範囲になり、値がただ１つに定まらないと考えておこう。
連立方程式の解き方との違い
解き方も連立方程式とは異なります。連立方程式では、加減法や代入法を利用して解を求めます。
しかし、連立不等式では、左辺と右辺に大小関係があるので、加減法や代入法を利用して解くことはしません。
連立不等式では、加減法や代入法を利用しない。同じ数を両辺に加減算できても、異なる数を両辺に加減算しても不等式が成り立つとは限らない。
連立不等式では、加減法や代入法を利用せずにそれぞれの不等式を個別に解きます。個別に解くので、それぞれの不等式を満たす解が個別に得られます。
連立不等式の解の求め方
不等式の解を個別に求めることはできましたが、本当に求めたいのは連立不等式の解です。連立不等式の解は、すべての不等式を満たす解です。
すべての不等式を満たす解は、それぞれ個別に求めた解の共通部分です。
連立不等式の解を見つけるには、数直線を利用します。
個別に求めた解を図示します。
解の不等号から、上限値や下限値を含むのかどうかが分かるように図示します。
その結果、閉じた範囲や開いた範囲などの共通部分ができます。
手順自体はそれほど難しくありません。求めた解をもとに数直線に描いて、その結果を正確に読み取れるようにしましょう。
連立不等式の解は、各不等式の解の共通部分。数直線を利用して求めよう。
連立不等式の解を求めるまでの流れ
連立不等式を解くときの流れをまとめると以下のようになります。
連立不等式を解く流れ
- それぞれの不等式を個別に解く。
- 不等式の解の共通部分を求める。
- 求めた共通部分が連立不等式の解。
共通部分を求めるとき、数直線を利用しよう。
共通部分を探すときのコツ
連立不等式を解くとき、解の共通部分を探すために数直線を利用します。解が示す値の範囲を可視化できるので、状況を把握しやすくなります。
解の共通部分を探すとき、ちょっとしたコツがあります。このコツを知っているだけでも共通部分を探しやすくなるでしょう。
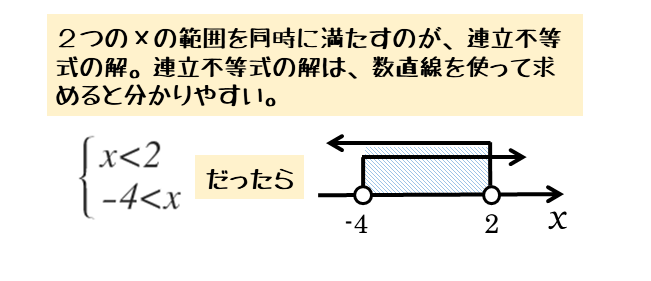
文字ｘについての１次不等式を２つ連立した連立不等式があるとします。このとき、１次不等式の解は２つ得られます。
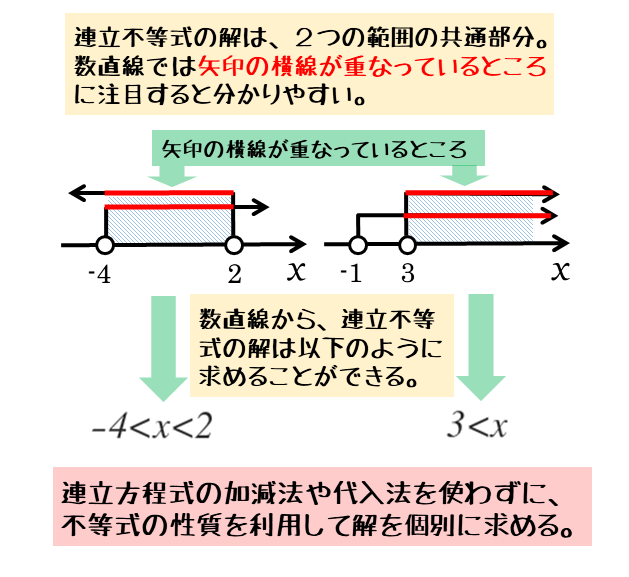
この２つの解を図示すると、矢印の横線が重なる部分があります。
図示した解は２つだったので、共通部分では矢印の横線も２つ重なっているはずです。
図示した解の数と、矢印の横線の重なる数は一致します。このことに注目すると、解の共通部分を探しやすくなります。
共通部分は、（図示した解の数）＝（矢印の横線の重なる数）になっている範囲。
次は連立不等式を扱った問題を解いてみましょう。
連立不等式の問題演習
次の連立不等式を解いてみましょう。
問１の解答・解説
問１
次の連立不等式を解け。
\begin{align*} \quad \left\{ \begin{array}{l} 2x+5 \lt 9 \\ 4x+2 \geqq x-1 \end{array} \right. \end{align*}一次不等式を個別に解きます。不等式の性質を利用して式変形し、文字ｘについてそれぞれ解きます。
問１の解答例
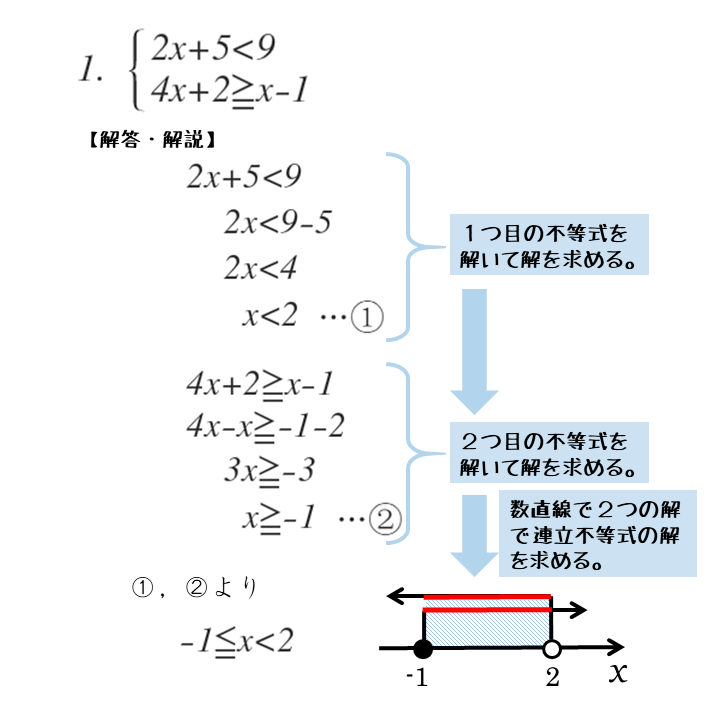
\begin{align*} \quad \left\{ \begin{array}{l} 2x+5 \lt 9 \quad \cdots \text{①} \\ 4x+2 \geqq x-1 \quad \cdots \text{②} \end{array} \right. \end{align*}①より
\begin{align*} &\quad 2x \lt 9-5 \\[ 7pt ] &\quad 2x \lt 4 \\[ 7pt ] &\quad x \lt 2 \end{align*}②より
\begin{align*} &\quad 4x-x \geqq -1-2 \\[ 7pt ] &\quad 3x \geqq -3 \\[ 7pt ] &\quad x \geqq -1 \end{align*}よって、連立不等式の解は
\begin{align*} \quad -1 \leqq x \lt 2 \end{align*}解（ｘが取り得る値の範囲）をそれぞれ求めたら、それらを数直線に図示します。すると、解の共通部分が見つかります。
この共通部分が連立不等式の解です。もし、重なる部分がない場合、連立不等式の解は「解なし」です。
問１のポイントと解答例をまとめると以下のようになります。
共通部分を探すとき、先ほどのコツを利用します。また、解が等号を含む場合は黒丸●、等号を含まない場合は白丸○を忘れないようにしましょう。
問２の解答・解説
問２
次の連立不等式を解け。
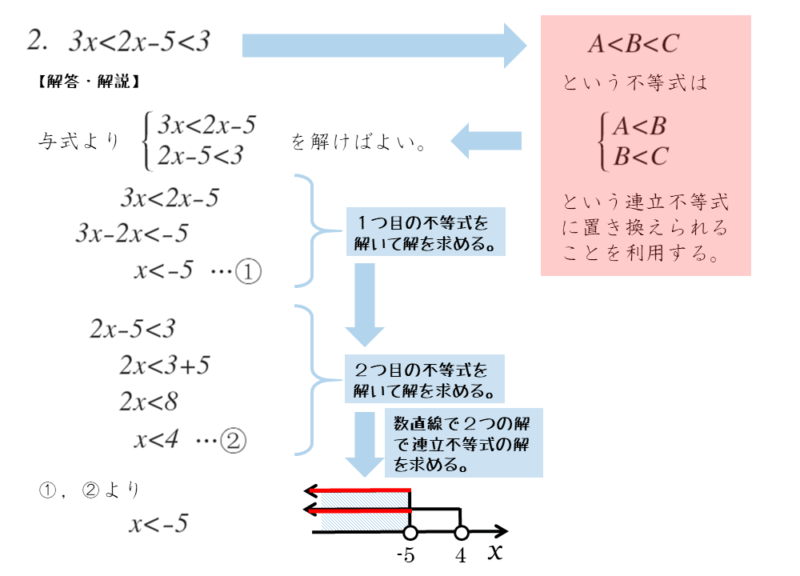
\begin{align*} \quad 3x \lt 2x-5 \lt 3 \end{align*}問２は、一見、連立不等式のようには見えませんが、連立不等式を１つの不等式で表すこともできます。
一般に、連立不等式が１つの式で表されているとき、以下のように基本的な表し方に書き換えます。
連立不等式が１つの式で表されているときの扱い
一般に、$A \lt B \lt C$ のとき
\begin{align*} \quad \left\{ \begin{array}{l} A \lt B \\ B \lt C \end{array} \right. \end{align*}これをもとにして、与式を書き換えると以下のようになります。
問２の解答例 1⃣
\begin{align*} \quad \quad 3x \lt 2x-5 \lt 3 \end{align*}より
\begin{align*} \quad \left\{ \begin{array}{l} 3x \lt 2x-5 \quad \cdots \text{①} \\ 2x-5 \lt 3 \quad \cdots \text{②} \end{array} \right. \end{align*}これで問１と同じ要領で解くことができます。この形への書き換えが問２のポイントです。
問１と同じように、一次不等式を個別に解きます。不等式の性質を利用して式変形し、ｘについて解きます。
問２の解答例 2⃣
\begin{align*} \quad \left\{ \begin{array}{l} 3x \lt 2x-5 \quad \cdots \text{①} \\ 2x-5 \lt 3 \quad \cdots \text{②} \end{array} \right. \end{align*}①より
\begin{align*} \quad 3x &\lt 2x-5 \\[ 7pt ] 3x-2x &\lt -5 \\[ 7pt ] x &\lt -5 \end{align*}②より
\begin{align*} \quad 2x-5 &\lt 3 \\[ 7pt ] 2x &\lt 3+5 \\[ 7pt ] 2x &\lt 8 \\[ 7pt ] x &\lt 4 \end{align*}よって、連立不等式の解は
\begin{align*} \quad x \lt -5 \end{align*}解の共通部分が、連立不等式の解になります。ここでは、数直線なしで解を求めていますが、数直線を利用した方が簡単で間違いも少ないです。
問２のポイントと解答例をまとめると以下のようになります。
連立不等式では、不等式を個別に解けば良いので、２つの式を一緒に扱う連立方程式よりも解きやすいかもしれません。
連立不等式を解くときに間違えやすいのは、解の共通部分を求めるところです。間違いを防ぐために、数直線を利用する習慣を付けておきましょう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学２・Ｂや数学３では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその１『合格る計算数学１・A・２・Ｂ』
オススメその２『鉄緑会 基礎力完成 数学Ⅰ・Ａ＋Ⅱ・Ｂ』
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごに、もう一度まとめ
- 連立不等式は、複数の不等式を組み合わせたもの。
- 連立不等式では、加減法や代入法を使わずに、不等式を個別に解く。
- 個別に解いた不等式の解の共通部分が、連立不等式の解。
- 共通部分を見つけるとき、数直線に図示する。
- 解の等号の有無に合わせて、図示するときに黒丸や白丸を使い分ける。