積分法|定積分と区分求積法の関係について

今回は数学3の区分求積法についてです。参考になれば幸いです。
区分求積法は面積や体積を求める方法の1つ
区分求積法は、面積や体積を求める方法の1つです。
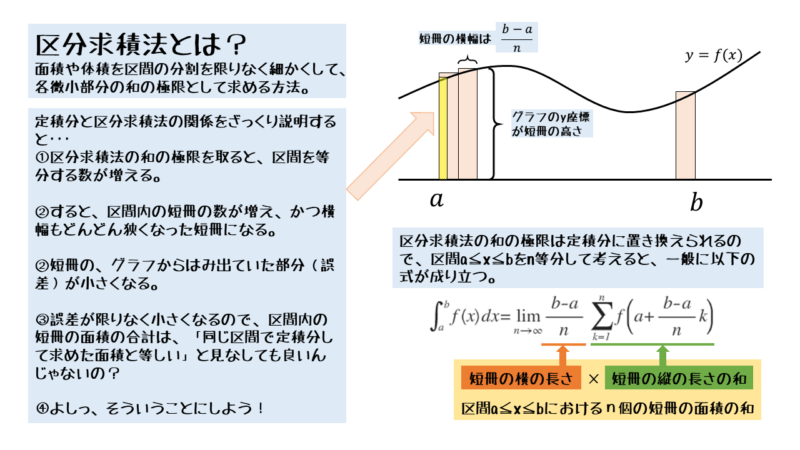
もう少し丁寧に言えば、区分求積法とは、面積や体積を区間の分割を限りなく細かくして、各微小部分の和の極限として求める方法です。
これだけではピンとこないかもしれませんが、大まかに説明すると次のようになります。
まず、求めたい図形の面積をスライスしていき、長方形の短冊の集まりに分割します。すると、長方形の短冊が横に並んだ状態になります。
この短冊はもとの面積を分割したものなので、その短冊の面積の和が求めたい図形の面積になります。しかし、長方形の短冊にしたので、隙間や出っ張りができます。厳密に言えば、もとの面積と等しいとは言えません。
そこで分割を限りなく細かくしていきます。分割した短冊はほとんど線になってしまいますが、徐々に隙間や出っ張りが限りなく小さくなります。つまり、求めたい図形の面積との誤差が限りなく小さくなります。
隙間や出っ張りが限りなく小さくなったところでそれらの和を取れば、もとの図形の面積とほとんど変わらないので等しいことにして良いよね?みたいな感じになります。
限りなく細かく分割した短冊の和は、もとの図形の面積と等しい。
これが分割を限りなく多くする、言い換えると極限を取ることのメリットです。
極限を取っている時点で、もうアバウトです。極限値でもイコールを使いますが、極限値はあくまでも近似値です。
これまで扱ってきた等式では両辺の値は等しいですが、極限値の場合は異なります。他の単元と違う感覚で接すると、極限値を理解しやすいかもしれません。
定積分で求めた面積とほとんど同じ
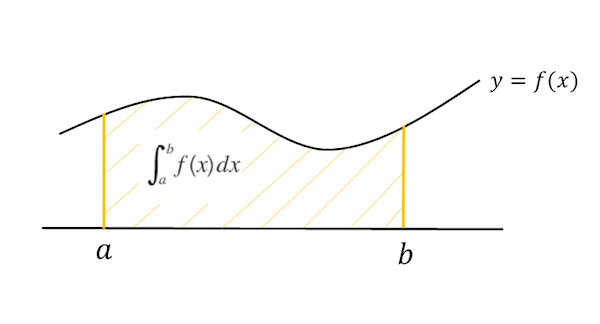
ある区間(たとえば、aからbまで)において、グラフとx軸とが挟む部分の面積(=定積分)は、図の斜線部分のようになります。
これと同じ区間で、区分求積法で求めた面積をx軸の挟む部分の面積(=定積分)と比較してみます。
ある区間(aからbまで)の定積分で求められる面積を区分求積法で考えるわけですから、n個の短冊にスライスして分割します。
短冊は長方形となるので、短冊の面積を「縦の長さ×横の長さ」で求めることができます。
このとき、短冊の横の長さ(=横幅)は、区間の長さb-aをn等分した長さです。
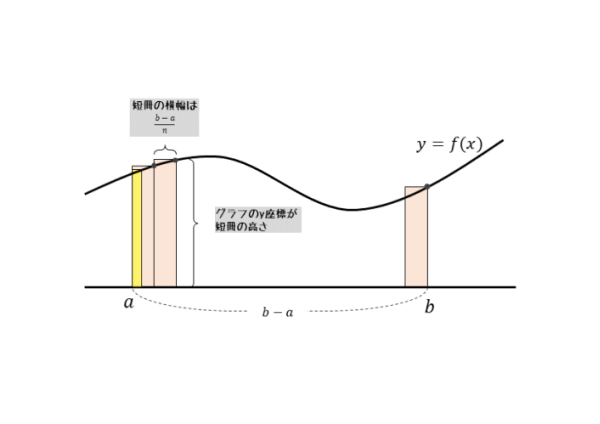
また、縦の長さは、図の場合であれば、短冊の右上にある頂点までの高さになります。この頂点はグラフ上の点なので、y座標が縦の長さに相当します。
短冊の横の長さは、区間の長さのn等分。縦の長さは、グラフ上の点のy座標。
図の短冊はざっくり作ったので、グラフからはみ出した部分があります。このまま和を求めても、定積分の値に等しくならないことは分かると思います。
しかし、分割数を10等分、100等分・・・と変えていけばどうなるでしょうか?
分割数が増えるのに伴って短冊の横幅が小さくなるので、はみ出した部分(誤差)も徐々に小さくなっていきます。
そうやって、等分するnの値を限りなく大きくすれば(極限を取れば)、短冊の横幅は限りなく小さくなります。その結果、はみ出した部分(誤差)も無視できるくらいに小さくなります。
そうなってしまえば、区分求積法を使って求めた面積は、定積分して求めた面積と等しいと見なせるようになるわけです。
この関係を式で表すと以下のようになります。
定積分と区分求積法の関係
\begin{align*} \int_{a}^{b} {f \left(x \right) dx} =\lim_{n \to \infty}{ \frac{b-a}{n} } \sum_{k=1}^{n}{f \left( a+\frac{b-a}{n} k \right)} \end{align*}左辺は、ある区間(a≦x≦b)における定積分を表し、右辺は、同じ区間における区分求積法による面積を表しています。右辺にシグマ(Σ)が出てきているのは、短冊の面積の和を求めているからです。
また、シグマ(Σ)の前にある分数は、区間の長さb-aをn等分したときの短冊の横幅を表します。
Σの前にある分数は短冊の横幅。この横幅は面積の和において共通因数となり、これをくくり出した後の式が右辺となる。結局、Σで和を取っているのは、短冊の縦の長さ(グラフのy座標)。
以上をまとめると以下のようになります。
次はよく出題される、具体的な区間で考えてみましょう。