図形と方程式|円の方程式の基本形と一般形について

円の方程式の基本形と一般形を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
次の円の方程式を求めよ。
$(1)$ 中心が $(3 \ , \ -4)$ で原点を通る円
$(2)$ 中心が $(1 \ , \ 2)$ で、$x$ 軸に接する円
$(3)$ $2$ 点 $(1 \ , \ 4) \ , \ (5 \ , \ 6)$ を直径の両端とする円
$(4)$ $2$ 点 $(2 \ , \ 1) \ , \ (1 \ , \ 2)$ を通り、中心が $x$ 軸上にある円
$(5)$ $3$ 点 $(4 \ , \ -1) \ , \ (6 \ , \ 3) \ , \ (-3 \ , \ 0)$ を通る円
問(1)の解答・解説
問(1)
次の円の方程式を求めよ。
中心が $(3 \ , \ -4)$ で原点を通る円
作図は以下の通りです。
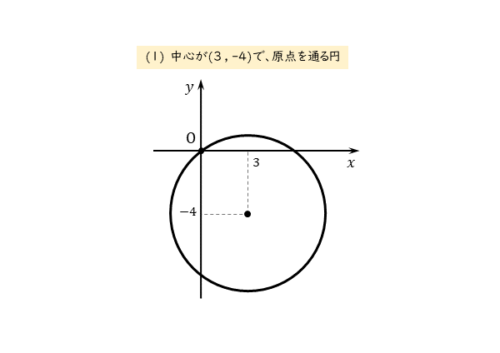
中心の座標が与えられているので、あとは半径が分かれば円の方程式が分かります。
半径の求め方については、図を見るとよく分かります。中心と円周上にある原点との距離が半径です。
問(1)の解答例 1⃣
中心と原点の距離は
\begin{align*} \quad \sqrt{\left(3-0 \right)^{2}+\left(-4-0 \right)^{2}}=5 \end{align*}これは半径に等しい。
半径が分かったら、中心の座標と半径を基本形に代入します。代入ミスに気を付けましょう。
問(1)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}中心が $(3 \ , \ -4)$ で、半径が $5$ となるので、求める円の方程式は
\begin{align*} \quad \left(x-3 \right)^{2}+\left\{y-\left(-4 \right) \right\}^{2}=5^{2} \end{align*}したがって
\begin{align*} \quad \left(x-3 \right)^{2}+\left(y+4 \right)^{2}=25 \end{align*}負の数を代入するときは要注意です。
問(2)の解答・解説
問(2)
次の円の方程式を求めよ。
中心が $(1 \ , \ 2)$ で、$x$ 軸に接する円
作図は以下の通りです。
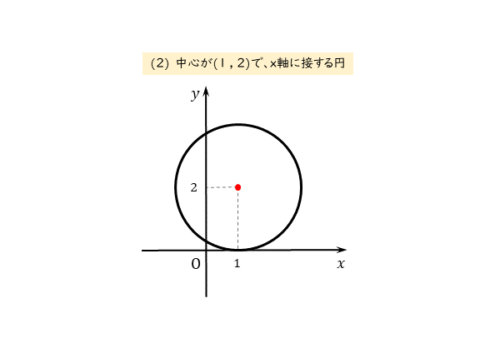
例題(1)と同じように、中心の座標が与えられていますが、半径が分かりません。円がx軸に接することを利用して、半径を求めます。
問(2)の解答例 1⃣
中心と $x$ 軸の距離は $2$ となる。
これは半径に等しい。
半径が分かったので、中心の座標と半径を基本形に代入します。
問(2)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}中心が $(1 \ , \ 2)$ で、半径が $2$ となるので、求める円の方程式は
\begin{align*} \quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=2^{2} \end{align*}したがって
\begin{align*} \quad \left(x-1 \right)^{2}+\left(y-2 \right)^{2}=4 \end{align*}x軸やy軸に接する円の半径は、中心の座標から求めることができます。
軸に接する円の半径
- x軸に接する円の半径 … |中心のy座標|が半径に等しい
- y軸に接する円の半径 … |中心のx座標|が半径に等しい
作図すればすぐに気付きますが、覚えておくと便利です。
問(3)の解答・解説
問(3)
次の円の方程式を求めよ。
$2$ 点 $(1 \ , \ 4) \ , \ (5 \ , \ 6)$ を直径の両端とする円
作図は以下の通りです。
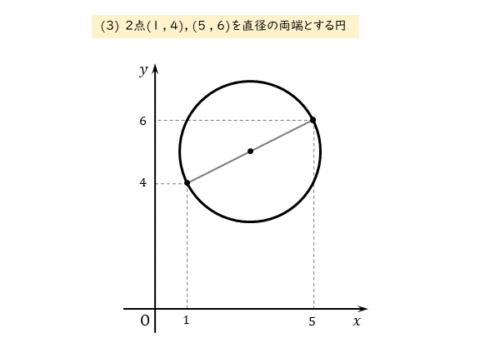
問(3)では、直径の両端となる2点の座標が与えられています。この2点を結ぶ線分が直径で、直径の中点が円の中心です。
上手く作図できれば、中心の座標を大まかに予想できます。
問(3)の解答例 1⃣
$2$ 点 $(1 \ , \ 4) \ , \ (5 \ , \ 6)$ を結ぶ線分の中点の座標は
\begin{align*} \quad \left(\frac{1+5}{2} \ , \ \frac{4+6}{2} \right) \end{align*}よって
\begin{align*} \quad (3 \ , \ 5) \end{align*}これが円の中心となる。
円の中心の座標が分かりました。この中心と直径の端点との距離が半径となります。両端の2点のうち、計算しやすい方を選びましょう。
両端の2点のうち一方を選んで半径を求めます。
問(3)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}半径は、中心 $(3 \ , \ 5)$ と点 $(1 \ , \ 4)$ の距離に等しいので
\begin{align*} \quad \sqrt{\left(1-3 \right)^{2}+\left(4-5 \right)^{2}}=\sqrt{5} \end{align*}中心の座標と半径が分かったので、基本形に代入します。
問(3)の解答例 3⃣
\begin{align*} \quad \vdots \end{align*}中心が $(3 \ , \ 5)$ で、半径が $\sqrt{5}$ となるので、求める円の方程式は
\begin{align*} \quad \left(x-3 \right)^{2}+\left(y-5 \right)^{2}=\left(\sqrt{5} \right)^{2} \end{align*}よって
\begin{align*} \quad \left(x-3 \right)^{2}+\left(y-5 \right)^{2}=5 \end{align*}円の方程式を基本形で表す問題であれば、それほど難易度は高くありません。
問(4)の解答・解説
問(4)
次の円の方程式を求めよ。
$2$ 点 $(2 \ , \ 1) \ , \ (1 \ , \ 2)$ を通り、中心が $x$ 軸上にある円
作図は以下の通りです。
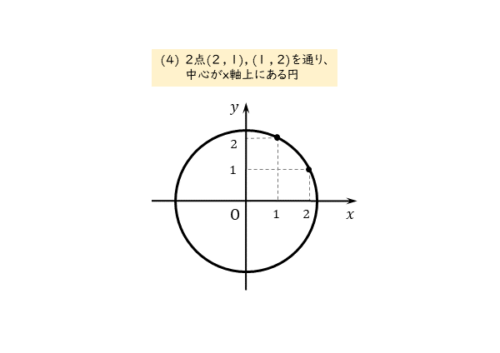
問(4)では、「中心」という言葉が出てきますが、座標は与えられていません。しかし、半径を求めるためにも中心の座標が必要です。ですから、中心の座標を自分で定義します。
中心がx軸上にあることに注意しましょう。
問(4)の解答例 1⃣
円の中心が $x$ 軸上にあるので、中心の座標を $(a \ , \ 0)$ とする。
x軸上にある点のy座標はつねに0であることに注意しましょう。
ここで、問題で与えられた2点は、円周上にあります。各点と中心の距離は、半径となるので等しくなります。このことを利用します。
問(4)の解答例 2⃣
\begin{align*} \quad \vdots \end{align*}$2$ 点 $(2 \ , \ 1) \ , \ (1 \ , \ 2)$ から中心 $(a \ , \ 0)$ へのそれぞれの距離が等しいので
\begin{align*} \quad \sqrt{\left(a-2 \right)^{2}+\left(0-1 \right)^{2}}=\sqrt{\left(a-1 \right)^{2}+\left(0-2 \right)^{2}} \end{align*}aについての方程式を導くことができました。これをaについて解きます。
問(4)の解答例 3⃣
\begin{align*} \quad \vdots \end{align*} \begin{align*} \quad \sqrt{\left(a-2 \right)^{2}+\left(0-1 \right)^{2}}=\sqrt{\left(a-1 \right)^{2}+\left(0-2 \right)^{2}} \end{align*}両辺を $2$ 乗すると
\begin{align*} \quad \left(a-2 \right)^{2}+\left(0-1 \right)^{2}=\left(a-1 \right)^{2}+\left(0-2 \right)^{2} \end{align*}整理すると
\begin{align*} &\quad \left(a-2 \right)^{2}+1=\left(a-1 \right)^{2}+4 \\[ 7pt ] &\quad \left(a-2 \right)^{2}-\left(a-1 \right)^{2}=3 \\[ 7pt ] &\quad \left\{\left(a-2 \right)-\left(a-1 \right) \right\} \left\{\left(a-2 \right)+\left(a-1 \right) \right\}=3 \\[ 7pt ] &\quad \left(-1 \right) \cdot \left(2a-3 \right)=3 \\[ 7pt ] &\quad 2a-3=-3 \\[ 7pt ] &\quad \therefore \ a=0 \end{align*}aは中心のx座標なので、中心が原点であることが分かります。次は半径を求めます。
問(4)の解答例 4⃣
\begin{align*} \quad \vdots \end{align*}$a=0$ から、半径は
\begin{align*} \quad \sqrt{\left(0-2 \right)^{2}+\left(0-1 \right)^{2}}=\sqrt{5} \end{align*}半径を求めるには、解答例 2⃣ の式の左辺、または右辺を利用します。
中心と半径の情報が揃ったので、基本形に代入します。
問(4)の解答例 5⃣
\begin{align*} \quad \vdots \end{align*}中心が $(0 \ , \ 0)$ で、半径が $\sqrt{5}$ となるので、求める円の方程式は
\begin{align*} \quad x^{2}+y^{2}=\left(\sqrt{5} \right)^{2} \end{align*}よって
\begin{align*} \quad x^{2}+y^{2}=5 \end{align*}中心が原点となるときの基本形に半径を代入しましょう。
中心が原点となる円の方程式
中心が原点、半径が $r$ のとき、円の方程式は
\begin{align*} \quad x^{2}+y^{2}=r^{2} \end{align*}










