図形と方程式｜共線や共点について

数学２

図形と方程式 直線

今回は、共線や共点について学習しましょう。複数の直線上にある点や、複数の点がのっている直線について学習します。

直線の方程式を求めたり、共有点の座標を求めたりします。不安な人は確認しながら進めましょう。

共線・共点

共線であること

与えられた点の集合がすべて同じ直線上にあるという性質を共線性と言います。また、与えられた点が共線性をもつとき、それらの点は共線であると言います。

「与えられた点が１つの直線を共有する」と捉えると、共線性を覚えやすいかもしれません。

共線の図
３点Ａ，Ｂ，Ｃは共線である

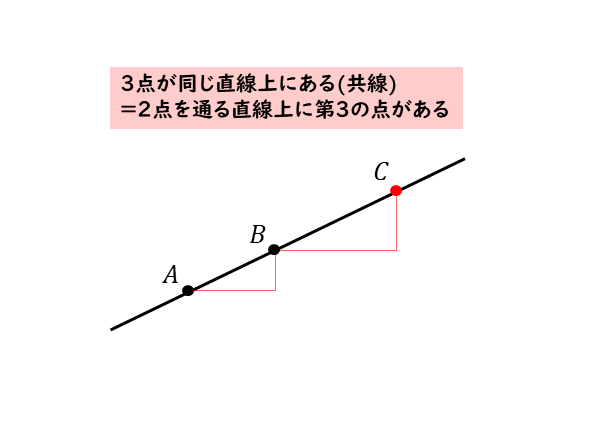
共線については、一般に３点が同じ直線上にあるときの話になります。３点が同じ直線上にあるというのは、言い換えると２点を通る直線上に第３の点があると考えることができます。

また、３点から２点を選んだときの傾きは３通りあります。３点が共線であるとき、３通りの傾きはすべて一致します。

上図において、たとえば２点Ａ，Ｂを通る直線の傾きと、２点Ｂ，Ｃを通る直線の傾きとが一致すれば、２つの直線は一致します。このとき、３点は共線であると言えます。

共線性は点のもつ性質のことなので、共線であるかどうかは３点が同じ直線上にあるかどうかという意味です。共線という言葉から直線のイメージが湧きますが、点に対する用語です。

「共線」という単語だけを覚えるのではなく、「３点が共線である」というフレーズで覚えましょう。

共線である

３点が同じ直線上にある＝２点を通る直線上に第３の点がある（＝２直線の傾きが一致する）

共点であること

点を共有するという性質のことを共点性と言います。同一の点を通る３本、または３本以上の直線が共点性をもつとき、それらの直線は共点であると言います。

「与えられた直線が１つの点を共有する」と捉えると、共点性を覚えやすいかもしれません。

共点の図
３直線は共点である

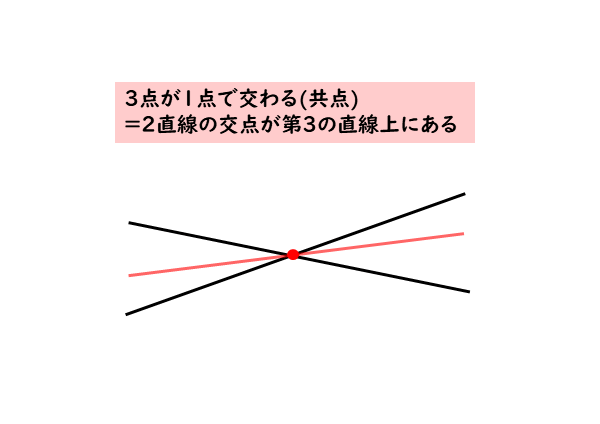
共点については、一般に３直線が１点で交わるときの話になります。３直線が１点で交わるというのは、言い換えると２直線の交点が第３の直線上にあると考えることができます。

共点性は直線のもつ性質のことなので、共点であるかどうかは３直線が１点で交わるかどうかという意味です。共点という言葉から点のイメージが湧きますが、直線に対する用語です。

「共点」という単語だけを覚えるのではなく、「３直線が共点である」というフレーズで覚えましょう。

共点である

３直線が１点で交わる＝２直線の交点が第３の直線上にある

共線や共点について考えてみよう

次の例題を考えてみましょう。

例題

$(1) \quad 3$ 点 $A(a \ , \ -2) \ , \ B(3 \ , \ 2) \ , \ C(-1 \ , \ 4)$ が同じ直線上にあるとき、定数 $a$ の値を求めよ。

$(2) \quad 3$ 直線 $2x+y+3=0 \ , \ x-y+6=0 \ , \ ax+y+24=0$ が $1$ 点で交わるとき、定数 $a$ の値を求めよ。

例題(1)の解答・解説

例題(1)

$3$ 点 $A(a \ , \ -2) \ , \ B(3 \ , \ 2) \ , \ C(-1 \ , \ 4)$ が同じ直線上にあるとき、定数 $a$ の値を求めよ。

例題(1)は「３点が共線である」ことに関する問題です。３点Ａ，Ｂ，Ｃが共線であることから、３点は同一直線上にあるはずです。

座標の分かる２点Ｂ，Ｃから、直線ＢＣの方程式を求め、この直線上に残りの点Ａがあると考えます。２点Ｂ，Ｃの座標から直線ＢＣの方程式を求めます。

例題(1)の解答例 1⃣

\begin{align*} &\text{$2$ 点 $B \ , \ C$ を通る直線 $BC$ の方程式は} \\[ 5pt ] &\quad y-2=\frac{4-2}{-1-3} \left(x-3 \right) \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad x+2y-7=0 \end{align*}

ここでは、直線ＢＣの方程式に分数が出てこないように、一般形で表しています。この直線上に点Ａがあれば、３点が同じ直線上にあると言えます。

点Ａの座標は直線ＢＣの方程式の解であるので、直線ＢＣの方程式に点Ａの座標を代入すると等式が成り立つはずです。このことを利用すると、定数ａについての方程式を導くことができます。

例題(1)の解答例 2⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad x+2y-7=0 \\[ 7pt ] &\text{直線 $BC$ 上に点 $A$ があるので} \\[ 5pt ] &\quad a+2 \cdot \left(-2 \right)-7=0 \\[ 7pt ] &\text{これを解くと} \\[ 5pt ] &\quad a=11 \end{align*}

例題(1)の別解・解説

初めから一般形を用いていれば分数が出てきません。分数を扱うのが苦手な場合は、以下の解法が良いでしょう。

例題(1)の別解例

\begin{align*} &\text{$2$ 点$B \ , \ C$ を通る直線 $BC$ の方程式は} \\[ 5pt ] &\quad \left(4-2 \right) \left(x-3 \right)-\left(-1-3 \right) \left(y-2 \right)=0 \\[ 7pt ] &\text{すなわち} \\[ 5pt ] &\quad 2 \left(x-3 \right)+4 \left(y-2 \right)=0 \\[ 7pt ] &\text{よって、} \\[ 5pt ] &\quad x+2y-7=0 \\[ 7pt ] &\text{直線 $BC$ 上に点 $A$ があるので} \\[ 5pt ] &\quad a+2 \cdot \left(-2 \right)-7=0 \\[ 7pt ] &\text{これを解くと} \\[ 5pt ] &\quad a=11 \end{align*}

２点を通る直線の方程式（公式）ですが、一般形で表すときの式です。

２点を通る直線の方程式

\begin{align*} &\text{異なる $2$ 点 $(x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2})$ を通る直線の方程式は} \\[ 5pt ] &\quad \left(y_{2}-y_{1} \right) \left(x-x_{1} \right)-\left(x_{2}-x_{1} \right) \left(y-y_{1} \right)=0 \end{align*}
関連記事

図形と方程式｜直線の方程式について

他の別解としては、「ＡＢの傾き＝ＢＣの傾き」を利用しても良いでしょう。ただし、ｘ軸に垂直な直線についての吟味が必要なので、あまりお勧めできません。

例題(1)の別解例

\begin{align*} &\text{$a=3$ のとき、直線 $AB$ は} \\[ 5pt ] &\quad x=3 \\[ 7pt ] &\text{このとき、点 $C$ は直線 $x=3$ 上にないので、} \\[ 5pt ] &\quad a \neq 3 \\[ 7pt ] &\text{$3$ 点 $A \ , \ B \ , \ C$ が同じ直線上にあるとき} \\[ 5pt ] &\quad \frac{2-(-2)}{3-a}=\frac{4-2}{-1-3} \\[ 7pt ] &\text{すなわち} \\[ 5pt ] &\quad \frac{4}{3-a}=-\frac{1}{2} \\[ 7pt ] &\text{これを解くと} \\[ 5pt ] &\quad a=11 \end{align*}

傾きを求めるとき、どうしても定数ａを含む文字式が分母に出てきます。定数ａを含む分母が０にならないことを示しておかなければなりません。この吟味が、ｘ軸に垂直な直線についての吟味に相当します。

例題(2)の解答・解説

例題(2)

$3$ 直線 $2x+y+3=0 \ , \ x-y+6=0 \ , \ ax+y+24=0$ が $1$ 点で交わるとき、定数 $a$ の値を求めよ。

例題(2)は「３直線が共点である」ことに関する問題です。３直線が共点であることから、３直線は１点で交わるはずです。

係数の分かる２直線から、交点の座標を求め、この交点が残りの直線上にあると考えます。係数や定数項が明らかな直線が２つ与えられているので、それらから交点の座標を求めます。

例題(2)の解答例 1⃣

\begin{align*} &\quad 2x+y+3=0 \quad \cdots \text{①} \\[ 7pt ] &\quad x-y+6=0 \quad \cdots \text{②} \\[ 7pt ] &\quad ax+y+24=0 \quad \cdots \text{③} \\[ 7pt ] &\text{とする。} \\[ 5pt ] &\text{$2$ 直線①，②の交点を $P$ とすると、その座標は} \\[ 5pt ] &\text{方程式①，②を連立して解けばよいので} \\[ 5pt ] &\text{①＋②より} \\[ 5pt ] &\quad x=-3 \\[ 7pt ] &\text{これと①より} \\[ 5pt ] &\quad y=3 \\[ 7pt ] &\text{よって} \\[ 5pt ] &\quad P \ (-3 \ , \ 3) \end{align*}

２直線①，②の交点Ｐは、直線③の上にもあります。このとき、点Ｐの座標は直線③の方程式の解であるので、点Ｐの座標を直線③の方程式に代入すると等式が成り立つはずです。

このことを利用して、定数ａについての方程式を導きます。

例題(2)の解答例 2⃣

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad ax+y+24=0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad P \ (-3 \ , \ 3) \\[ 7pt ] &\text{点 $P$ は直線③上にもあるので、} \\[ 5pt ] &\quad a \cdot \left(-3 \right)+3+24=0 \\[ 7pt ] &\text{これを解くと} \\[ 5pt ] &\quad a=9 \end{align*}

ここで終わりではありません。共点であるとは、３本または３本以上の直線が１点で交わることです。直線③が他の直線①，②と一致しないことを確認します。

例題(2)の解答例 3⃣

\begin{align*} &\quad 2x+y+3=0 \quad \cdots \text{①} \\[ 7pt ] &\quad x-y+6=0 \quad \cdots \text{②} \\[ 7pt ] &\quad ax+y+24=0 \quad \cdots \text{③} \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\quad a=9 \\[ 7pt ] &\text{このとき、直線③の方程式は} \\[ 5pt ] &\quad 9x+y+24=0 \\[ 7pt ] &\text{となり、直線①，②とは一致しない。} \\[ 5pt ] &\text{したがって、求める $a$ の値は} \\[ 5pt ] &\quad \therefore \ a=9 \end{align*}

直線③が直線①または直線②と一致すると、「３本または３本以上の直線が１点で交わる」ことを満たしません。検算にもなるので、さいごの確かめを忘れないようにしましょう。

次は、共線や共点を扱った問題を実際に解いてみましょう。

数学２直線,図形と方程式,共線,共点

Posted by kiri