数学2
座標を利用した証明を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
\begin{align*}
&(1) \quad \text{$\triangle {ABC}$ の辺 $BC$ の中点を $M$ とするとき、} \\[ 5pt ]
&\quad \quad AB^{\scriptsize{2}}+AC^{\scriptsize{2}}=2 \left( AM^{\scriptsize{2}}+BM^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{が成り立つことを証明せよ。} \\[ 10pt ]
&(2) \quad \text{$\triangle {ABC}$ において、辺 $BC$ を $3:2$ に内分する} \\[ 5pt ]
&\text{点を $D$ とする。このとき、} \\[ 5pt ]
&\quad \quad 3 \left( 2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \right)=5 \left( 3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{が成り立つことを証明せよ。}
\end{align*}
問(1)の解答・解説
問(1)
\begin{align*}
&\text{$\triangle {ABC}$ の辺 $BC$ の中点を $M$ とするとき、} \\[ 7pt ]
&\quad AB^{\scriptsize{2}}+AC^{\scriptsize{2}}=2 \left( AM^{\scriptsize{2}}+BM^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{が成り立つことを証明せよ。}
\end{align*}
例題と同じ要領で座標軸を定めます。
問(1)の解答例 1⃣
\begin{align*}
&\text{直線 $BC$ を $x$ 軸に、辺 $BC$ の垂直二等分線を} \\[ 5pt ]
&\text{$y$ 軸にとると、中点 $M$ は原点 $O$ になる。}
\end{align*}
座標軸が定まったら、点の座標を定義します。変数をできるだけ少なくしましょう。
問(1)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{$3$ 点 $A \ , \ B \ , \ C$ の座標を} \\[ 5pt ]
&\quad A \ (a \ , \ b) \ , \ B \ (-c \ , \ 0) \ , \ C \ (c \ , \ 0) \\[ 7pt ]
&\text{と表すことができる。}
\end{align*}
問(1)では、重心Gが出てこないので、解答例のように頂点Aの座標を定義します。また、頂点B,Cの座標は原点(またはy軸)に関して対称なので、同じ変数を利用します。
作図すると以下の通りです。作図は、答案を作成する前に済ませておきましょう。
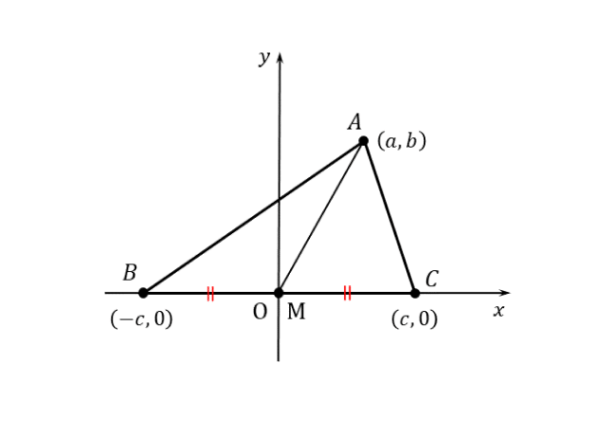 問(1)の作図
問(1)の作図 座標軸や座標が定まれば、後は計算だけです。必ず等式が成り立つはずなので、焦らず計算しましょう。左辺を計算します。
問(1)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad A \ (a \ , \ b) \ , \ B \ (-c \ , \ 0) \ , \ C \ (c \ , \ 0) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\text{このとき} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}+AC^{\scriptsize{2}} \\[ 7pt ]
&\quad =\left\{ \left(-c-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\}+\left\{ \left(c-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =\left\{ \left(c+a \right)^{\scriptsize{2}}+b^{\scriptsize{2}} \right\}+\left\{ \left(c-a \right)^{\scriptsize{2}}+b^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =\left(c^{\scriptsize{2}}+2ca+a^{\scriptsize{2}}+b^{\scriptsize{2}} \right)+\left(c^{\scriptsize{2}}-2ca+a^{\scriptsize{2}}+b^{\scriptsize{2}} \right) \\[ 7pt ]
&\quad =2 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+c^{\scriptsize{2}} \right) \quad \cdots \text{①}
\end{align*}
同様にして、右辺を計算します。
問(1)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad A \ (a \ , \ b) \ , \ B \ (-c \ , \ 0) \ , \ C \ (c \ , \ 0) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =2 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+c^{\scriptsize{2}} \right) \quad \cdots \text{①} \\[ 7pt ]
&\text{また} \\[ 5pt ]
&\quad AM^{\scriptsize{2}}+BM^{\scriptsize{2}} \\[ 7pt ]
&\quad =\left\{ \left(0-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\}+\left\{ 0-\left(-c \right) \right\}^{\scriptsize{2}} \\[ 7pt ]
&\quad =\left(a^{\scriptsize{2}}+b^{\scriptsize{2}} \right)+c^{\scriptsize{2}} \\[ 7pt ]
&\quad =a^{\scriptsize{2}}+b^{\scriptsize{2}}+c^{\scriptsize{2}} \quad \cdots \text{②}
\end{align*}
線分BMは、x軸上にある2点間の距離なので、x座標の差で表されます。
与式を導くには、②式を①式に代入します。すると、等式が成り立つことを示せます。
問(1)の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad =2 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+c^{\scriptsize{2}} \right) \quad \cdots \text{①} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =a^{\scriptsize{2}}+b^{\scriptsize{2}}+c^{\scriptsize{2}} \quad \cdots \text{②} \\[ 7pt ]
&\text{①,②より} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}+AC^{\scriptsize{2}}=2 \left( AM^{\scriptsize{2}}+BM^{\scriptsize{2}} \right)
\end{align*}
この等式を中線定理と言います。また、パップスの定理と言うこともあります。意外と役立つ等式なので、覚えておくと良いでしょう。
問(2)の解答・解説
問(2)
\begin{align*}
&\text{$\triangle {ABC}$ において、辺 $BC$ を $3:2$ に内分する} \\[ 5pt ]
&\text{点を $D$ とする。このとき、} \\[ 7pt ]
&\quad 3 \left( 2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \right)=5 \left( 3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{が成り立つことを証明せよ。}
\end{align*}
座標軸を定めます。このとき、点Dは中点ではありませんが、原点と重なるようにします。
問(2)の解答例 1⃣
\begin{align*}
&\text{直線 $BC$ を $x$ 軸に、点 $D$ を通り、直線 $BC$ に垂直な} \\[ 5pt ]
&\text{直線を $y$ 軸にとると、点 $D$ は原点 $O$ になる。}
\end{align*}
座標軸が定まったら、点の座標を定義します。もちろん「変数はできるだけ少なく」です。
問(2)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\text{よって、$3$ 点 $A \ , \ B \ , \ C$ の座標を} \\[ 5pt ]
&\quad A \ (a \ , \ b) \ , \ B \ (-3c \ , \ 0) \ , \ C \ (2c \ , \ 0) \\[ 7pt ]
&\text{と表すことができる。}
\end{align*}
点B,Cの座標に注意しましょう。同じ文字を用いることができますが、点Dが辺BCを3:2に内分する点なので、原点に関して対称ではありません。
作図すると以下の通りです。答案を作成する前に作図を済ませておきましょう。
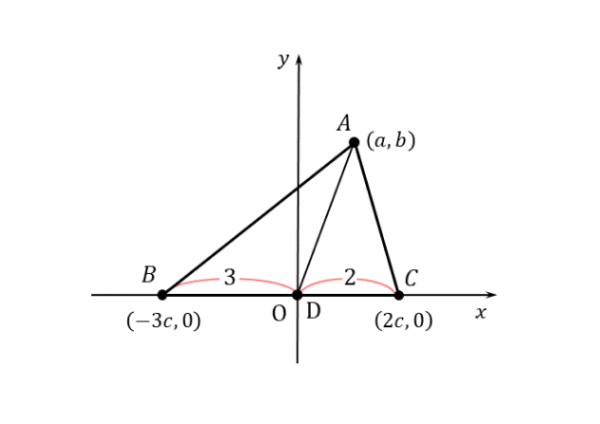 問(2)の作図
問(2)の作図 座標軸や座標が定まれば、左辺と右辺をそれぞれ計算します。等式の証明問題なので、必ず等式が成り立ちます。焦らず計算しましょう。左辺から計算します。
問(2)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad A \ (a \ , \ b) \ , \ B \ (-3c \ , \ 0) \ , \ C \ (2c \ , \ 0) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\text{このとき} \\[ 5pt ]
&\quad 2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \\[ 7pt ]
&\quad =2 \left\{ \left(-3c-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\}+3 \left\{ \left(2c-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =2 \left\{ \left(3c+a \right)^{\scriptsize{2}}+b^{\scriptsize{2}} \right\}+3 \left\{ \left(2c-a \right)^{\scriptsize{2}}+b^{\scriptsize{2}} \right\} \\[ 7pt ]
&\quad =2 \left(9c^{\scriptsize{2}}+6ca+a^{\scriptsize{2}}+b^{\scriptsize{2}} \right)+3 \left(4c^{\scriptsize{2}}-4ca+a^{\scriptsize{2}}+b^{\scriptsize{2}} \right) \\[ 7pt ]
&\quad =5a^{\scriptsize{2}}+5b^{\scriptsize{2}}+30c^{\scriptsize{2}} \\[ 7pt ]
&\quad =5 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}} \right) \quad \cdots \text{①}
\end{align*}
同様にして、右辺を計算します。
問(2)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad A \ (a \ , \ b) \ , \ B \ (-3c \ , \ 0) \ , \ C \ (2c \ , \ 0) \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =5 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}} \right) \quad \cdots \text{①} \\[ 7pt ]
&\text{また} \\[ 5pt ]
&\quad 3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \\[ 7pt ]
&\quad =3 \left\{ \left(0-a \right)^{\scriptsize{2}}+\left(0-b \right)^{\scriptsize{2}} \right\}+2 \left\{ 0-\left(-3c \right) \right\}^{\scriptsize{2}} \\[ 7pt ]
&\quad =3 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}} \right)+2 \cdot 9c^{\scriptsize{2}} \\[ 7pt ]
&\quad =3\left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}} \right) \quad \cdots \text{②}
\end{align*}
線分BDは、x軸上にある2点間の距離なので、x座標の差で表されます。
与式を導くには、①,②式を変形する必要があります。①,②式には共通の式があるので、それを利用すると等式が成り立つことを示せます。
問(2)の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad 2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =5 \left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}} \right) \quad \cdots \text{①} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad 3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad =3\left(a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}} \right) \quad \cdots \text{②} \\[ 7pt ]
&\text{①より} \\[ 5pt ]
&\quad a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}}= \frac{1}{5} \left(2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{②より} \\[ 5pt ]
&\quad a^{\scriptsize{2}}+b^{\scriptsize{2}}+6c^{\scriptsize{2}}= \frac{1}{3} \left(3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad \frac{1}{5} \left(2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \right)=\frac{1}{3} \left(3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \right) \\[ 7pt ]
&\text{したがって} \\[ 5pt ]
&\quad 3 \left( 2AB^{\scriptsize{2}}+3AC^{\scriptsize{2}} \right)=5 \left( 3AD^{\scriptsize{2}}+2BD^{\scriptsize{2}} \right)
\end{align*}
左辺と右辺の計算では、素直に展開するだけではなく、共通因数でくくるなどして要領よく計算しましょう。
Recommended books
チャート式と言えば有名ですが、学校で配布されるのは、ほとんどが黄色か青色のどちらかです。数学を苦手にしている人にとっては、扱い辛く感じるかもしれません。ページ数も多いので尚更です。
オススメ その1
日常学習では辞書的に利用できる参考書があると助かります。有名なのは、チャート式でしょう。
チャート式は、色別にレベル分けされています。学校で配布されるのは、青や黄のチャート式が多いと思います。ただし、青や黄の内容が高度だと感じるのであれば、いっそのこと白のチャート式の方が良いかもしれません。
『チャート式基礎と演習数学1+A 増補改訂版』や『チャート式基礎と演習数学2+B 増補改訂版』では、より基礎的な内容が扱われています。教科書の内容を補完してくれるので、予習や復習を進めやすくなるでしょう。
基礎固めには白チャート。数学の苦手な生徒でも,安心して学習を進められます。教科書と併用しながらの学習や、基礎固めには最適の参考書。中堅私立大学の受験対策や、大学入学共通テストの準備にも役立つ一冊。本冊巻末に、大学入学共通テストの対策ができる「実践編」を追加。
オススメ その2
白チャートと同じように基礎的な内容を扱っているのが、スカイチャートと言われる『チャート式 絶対に身につけたい数学1+Aの基本』や『チャート式 絶対に身につけたい数学2+Bの基本』です。速習型の参考書なので、たとえば、受験勉強を何から始めれば良いのか分からない人向けの教材です。
白チャート『チャート式基礎と演習数学1+A 増補改訂版』は、560ページ(別冊解答編368ページ)あります。青チャートだと640ページ(別冊解答編404ページ)なので、白チャートも少ない方です。これらに対して、スカイチャート『チャート式 絶対に身につけたい数学1+Aの基本』は160ページ(別冊解答編88ページ)なので、かなりコンパクトにまとめられています。
使い方としては、予習や復習の際に類題をこなしたり、定期考査前の確認や仕上げに使ったりできます。また、受験勉強の準備にあたって、自分の基礎学力を短期間で確認することができます。
対象 … 教科書の内容を効率的に総復習したい人や、基礎知識を総整理したい人
特長 … 絶対に身につけたい基礎知識が詰まった良問を精選しました。「極意」では,問題を解くとき、効果的にアプローチするための手順や考え方をコンパクトにまとめました。例題と同等のレベルである練習問題を解くことで,例題の解法や基礎知識の理解度を確認できます。
参考書は紹介した教材だけではありません。大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 等式の証明では、座標を利用すると簡単な場合がある。
- 座標軸の定め方に注意しよう。
- 中点や内分点が原点と重なるようにしよう。
- 三角形の底辺がx軸と重なるようにしよう。
- 対称性を利用するなどして、変数をできるだけ少なくして座標を決めよう。



















