数と式｜一次不等式を扱った応用問題を解いてみようその１（立式の基本）

08/23/2023数学１

一次不等式を扱った応用問題を解いてみよう

次の問題を解いてみましょう。

第１問の解答・解説

第１問

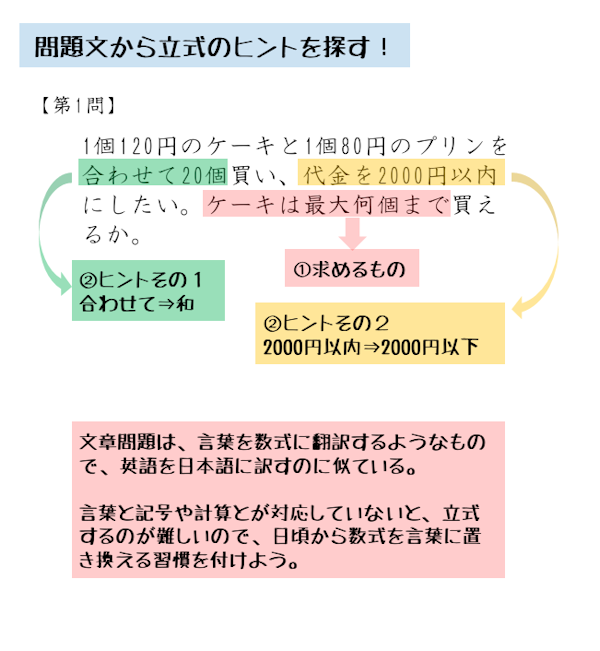
$1$ 個 $120$ 円のケーキと $1$ 個 $80$ 円のプリンを合わせて $20$ 個買い、代金を $2000$ 円以内にしたい。ケーキは最大何個まで買えるか。

まずは一読して求める数量が何かを探しましょう。求める数量は文章の最後に提示してあることがほとんどです。また、文章中からヒントを見つけます。

文章中のヒント

求める数量：ケーキの最大個数
ヒント１：ケーキとプリンを合わせて２０個（単位は個数）
ヒント２：支払う代金は２０００円以内（単位は円）

第１問では、ケーキの最大個数を求めたいので、ケーキの個数の範囲を求めれば良さそうです。購入するケーキの個数をｘ個とします。

また、文章中に「代金が２０００円以内」とありますが、言い換えると、「代金が２０００円以下」ということです。「～以下」という言い回しが出てきたので、不等式で立式しようと方針が立ちます。

式の形

（支払う代金）$\leqq \ 2000$

式の形が決まったので、部分的に見ていきます。左辺は「ケーキとプリンを購入した代金」です。

ケーキとプリンの１個の値段が異なるので、代金を別々に求める必要があります。ですから、左辺の支払う代金は、ケーキとプリンの代金の和で表されます。

左辺

（支払う代金）$=$（ケーキの代金）$+$（プリンの代金）

ケーキを買う個数をｘ個とすると、ケーキの代金を求めることができます。それに対して、プリンの個数はまだ分かっていません。

そこで、「ケーキとプリンを合わせて２０個」というヒントを利用して求めます。

プリンの個数

（ケーキの個数）$+$（プリンの個数）$=20$

より

（プリンの個数）$=20-$（ケーキの個数）

ケーキとプリンの個数の関係から、プリンの個数はケーキの個数ｘを用いて（２０－ｘ）個と表されます。

ケーキとプリンの１個の値段はすでに与えられているので、それぞれの代金を求めることができます。そして代金の和を取れば、支払った代金になります。

支払った代金

ケーキの個数を $x$ とすると、代金は

\begin{align*} \quad 120 \times x=120x \quad \text{（円）} \end{align*}

また、プリンの個数は

\begin{align*} \quad \left(20-x \right) \quad \text{（個）} \end{align*}

となるので、代金は

\begin{align*} \quad 80 \times \left(20-x \right)=80\left(20-x \right) \quad \text{（円）} \end{align*}

よって、支払う代金は

\begin{align*} \quad 120x+80\left(20-x \right) \quad \text{（円）} \end{align*}

支払う代金が２０００円以下になれば良いので、不等式で立式します。

不等式で立式する

支払う代金は $2000$ 円以内なので

\begin{align*} \quad 120x+80\left(20-x \right) \leqq 2000 \end{align*}

立式すると、ｘについての一次不等式を導出できました。この不等式の解がｘの取りうる値の範囲、すなわちケーキの個数の取り得る範囲です。範囲の最大値がケーキの最大個数です。

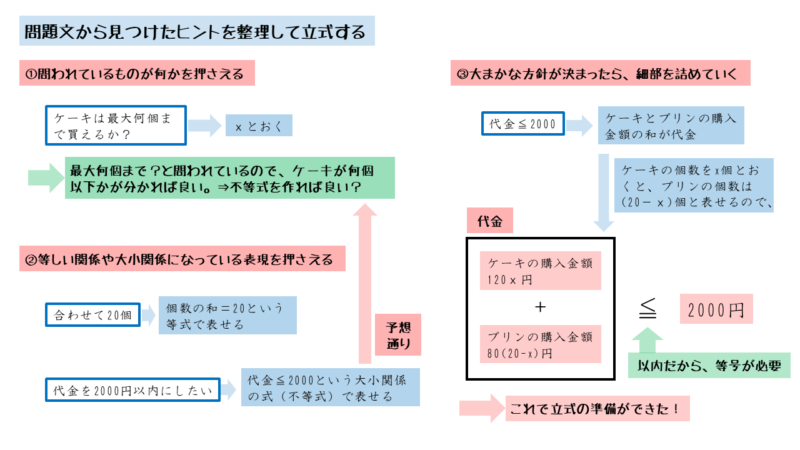
ヒントの読み取りから立式までの流れをまとめると以下のようになります。

また、第１問のポイントと解答例をまとめると以下のようになります。

暗黙の条件に注意しよう

解を求めた後に注意したいのが、文章中に明記されない暗黙の条件です。

第１問では必要ありませんでしたが、たとえば、個数であれば「自然数」という条件が存在しています。このような条件が解の吟味に必要なときがあります。

扱う数量によって、文章中に明記されていない暗黙の条件が存在するので注意しよう。

第２問の解答・解説

第２問

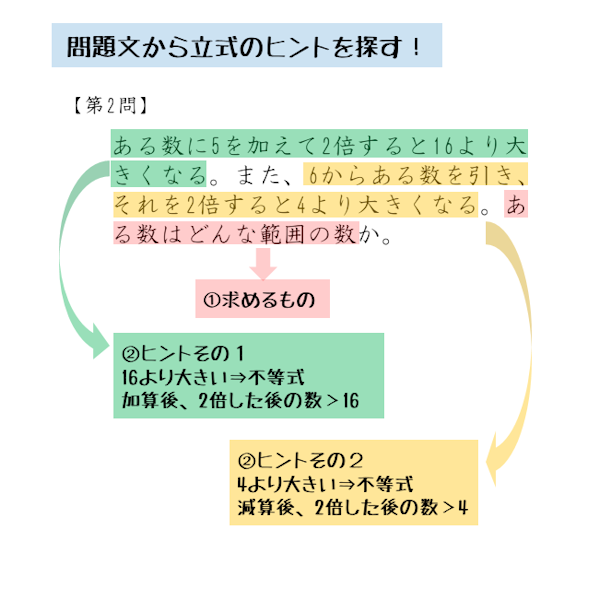
ある数に $5$ を加えて $2$ 倍すると $16$ より大きくなる。また、$6$ からある数を引き、それを $2$ 倍すると $4$ より大きくなる。ある数はどんな範囲の数か。

一読して求める数量が何かを探しましょう。また、文章中からヒントを見つけます。

文章中のヒント

求める数量：ある数の範囲
ヒント１：ある数に５を加えて２倍すると１６より大きい
ヒント２：６からある数を引き、それを２倍すると４より大きい

第２問では、「ある数の範囲」を求めたいので、ある数をｘとおきます。

さらに、接続詞「また」に注目すると、ある数を使った計算の話が２つあることに気付きます。ある数を求めるためのヒントが２つあるということです。

大小関係の話なので、不等式で表すことができそうです。これで式の形が決まりました。不等式が２つできることが分かります。

式の形

ヒント１から

ある数に $5$ を加えて $2$ 倍した後の数）$\gt \ 16$

ヒント２から

（$6$ からある数を引き、それを $2$ 倍した後の数）$\gt \ 4$

式の形が決まったので、部分的に見ていきます。ヒント１，２の左辺に注目します。

ここで、注意したいのは計算の順序です。どちらのヒントでも、２倍するのは加算や減算した後の数に対してです。

ヒント１では、ある数ｘに５を加えるので、（ｘ＋５）という数になります。この数（ｘ＋５）を２倍します。ヒント２では、６からある数ｘを引くので、（６－ｘ）という数になります。この数（６－ｘ）を２倍します。

左辺の立式

ヒント１の左辺

ある数 $x$ に $5$ を加えると

\begin{align*} \quad x+5 \end{align*}

これを $2$ 倍するので

\begin{align*} \quad \left(x+5 \right) \times 2 \end{align*}

ヒント２の左辺

$6$ からある数 $x$ を引くと

\begin{align*} \quad 6-x \end{align*}

これを $2$ 倍するので

\begin{align*} \quad \left(6-x \right) \times 2 \end{align*}

加算や減算した後の数は多項式になり、この多項式を２倍しなければなりません。

多項式をカッコでくくっておかないと、計算の意味や順序が変わってしまいます。ｘだけを２倍したり、５だけを２倍したりしないように注意しましょう。

計算の意味や順序が変わる例

ヒント１の左辺の間違い

\begin{align*} \quad x + 5 \times 2 \end{align*}

⇒ $x$ に、$5$ を $2$ 倍して加える（加えた数）

ヒント２の左辺の間違い

\begin{align*} \quad 6 \ – x \times 2 \end{align*}

⇒ $6$ から、$x$ を $2$ 倍して引く（引いた数）

ヒント１，２について、それぞれ不等式で立式します。

不等式で立式する

ある数 $x$ に $5$ を加えると

\begin{align*} \quad x+5 \end{align*}

これを $2$ 倍するので

\begin{align*} \quad \left(x+5 \right) \times 2 \end{align*}

すなわち

\begin{align*} \quad 2\left(x+5 \right) \end{align*}

これが$16$ より大きくなるので

\begin{align*} \quad 2\left(x+5 \right) \gt 16 \end{align*}

$6$ からある数 $x$ を引くと

\begin{align*} \quad 6-x \end{align*}

これを $2$ 倍するので

\begin{align*} \quad \left(6-x \right) \times 2 \end{align*}

すなわち

\begin{align*} \quad 2\left(6-x \right) \end{align*}

これが $4$ より大きくなるので

\begin{align*} \quad 2\left(6-x \right) \gt 4 \end{align*}

ところで、ヒント１，２はある数を使った計算の話であるので、ある数ｘについてどちらも成り立たなければなりません。ですから、第２問は連立不等式の問題です。

連立不等式の解は、それぞれの不等式の解の共通部分です。これが求める数の範囲になります。

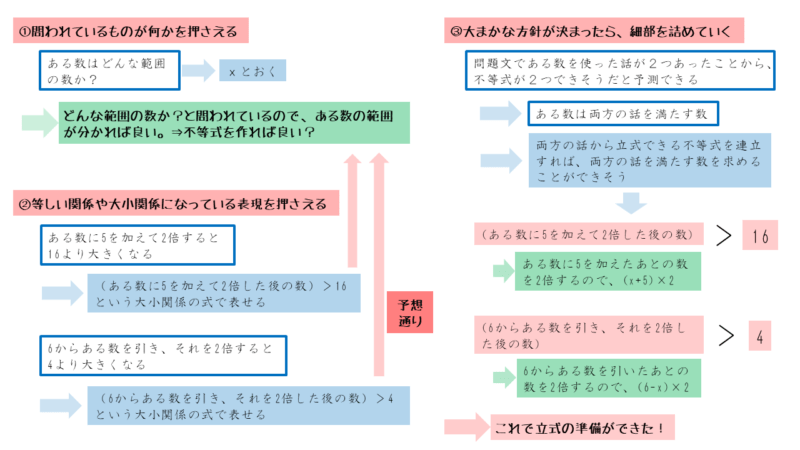
ヒントの読み取りから立式までの流れをまとめると以下のようになります。

第２問のポイントと解答例をまとめると以下のようになります。

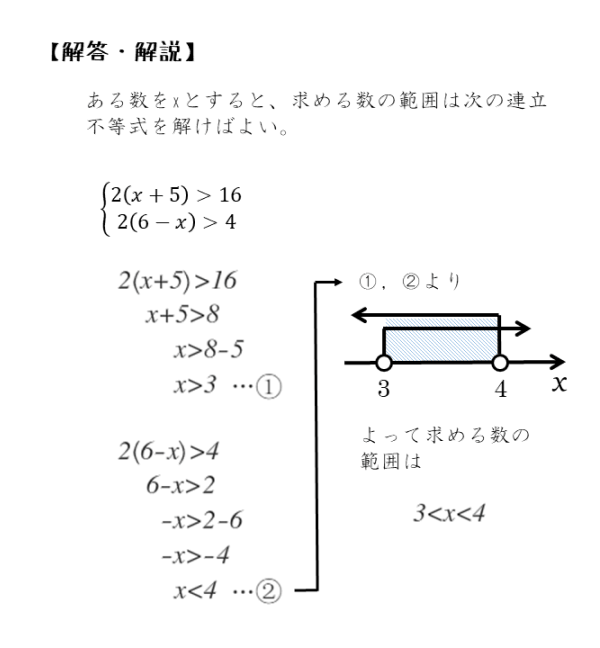
ある数ｘの範囲は、自然数や整数などが含まれない範囲３＜ｘ＜４となります。文章中には、自然数や整数などの条件がなく、また、それを明示する表現もありません。ですから、実数の範囲での話だと考えられます。

他にも一次不等式の文章問題を紹介しているので、ぜひチャレンジしてみましょう。

以下、余談です。

文章問題を解きこなすために

英作文では日本語を英語に置き換えています。それと同じことを数学でもやるだけです。

言葉を数式に翻訳するイメージです。そのためには、記号や数式の意味を言葉に置き換える訓練が必要です。

日頃の学習では、定義をしっかり覚えることを第一に、文言から数式化したり、数式を言語化したりすると良いでしょう。

読解力の有無も意外と関係がありそう

どの科目でも理解するための基礎になるのが、主に語彙力や読解力ではないでしょうか。

数学で言えば、語彙力は用語や記号などの定義を知っており、それを適切に使える力、読解力は数量の関係や問題の要求（求められている答え）などを読み取る力だと考えられます。

設問は日本語で書かれているわけですから、読めないわけではありません。それにも関わらず内容を理解できなかったり、誤読したりするのであれば、語彙力や読解力が足りない可能性があります。

何となく読めるではなく、設問の意図するものを正しく汲み取ることが本当の「読める」だと考えられます。

語彙力や読解力を付けるためには、解けない問題に出会ったとき、自分がどこで躓いているかを１つ１つ点検することが大切です。

躓きの中身を知らなければ、自分の足りない部分に気付けません。何となく分からないまま、解けないままだから、語彙力や読解力がいつまで経っても伸びないのかもしれません。

躓きは誰にでもありますが、そこでの対応の仕方でその後の伸びが変わってきます。

Recommended books

大学進学を考えたとき、記述を重視した学習を日常的に行った方が良いでしょう。試験の難易度は、マーク形式よりも記述形式の方が高いからです。

また、記述では思考力や表現力などが必要で、それらを身に付けるのは一朝一夕には難しいことも理由の１つです。

記述の訓練は、基本的に教科書や参考書の例題を真似することから始まりますが、記号の使い分けや独特の表現などがあり、手探りで進めていくのは大変です。

そこでお勧めしたいのが以下の２冊です。記述の訓練に特化したテキストになります。

オススメその１

１冊目は『基礎からのジャンプアップノート数学記述式答案書き方ドリル』で、数学に苦手意識のある人におすすめです。

数学Ⅰ＋Ａ＋Ⅱ＋Ｂの記述力の基礎力を固めるなら、まずはこのドリルから！！

問題編６４ページ、別冊解答編３２ページ

証明問題、場合分けの答案の書き方のコツがわかる

「なぞって理解する」書き込みノートだから、わかりやすい答案の書き方が覚えやすい

「例（手本）」→「Check！」→「練習問題」　まねる＆繰り返すの流れで、記述力UP！

別冊「解答編」では、練習問題をくわしく解答

基礎からのジャンプアップノート数学記述式答案書き方ドリル

created by Rinker

『基礎からのジャンプアップノート』は数学以外の科目にもあります。基礎レベルの内容を扱っており、ページ数も多くありません。日常学習での予習や復習に使い勝手が良いでしょう。

オススメその２

２冊目は『総合的研究記述式答案の書き方ーー数学I・A・II・B』です。数学に苦手意識がなく、将来的に得意科目にしたい人向けです。

『総合的研究』シリーズは、チャート式やフォーカスゴールドなどと並んで有名な参考書で、数学以外の科目もあります。また、電子書籍でも出版されているので、持ち運びに苦労しないのもポイントが高いです。

この本のテーマは《伝える》ことです。私たちは、この本で、数学的に正当な思考・数学的な事実を、どうすれば文章にして他者に伝えられるか、懸命に説明しています。

ちょっとした言葉づかい、論理的な説明の順序、条件と命題の違いの意識、いろいろな文字の立場の理解・・・・・・きっと、読者の皆さんの考えを読み手に《伝える》ために、すぐ役立つはずです。

（中略）数学の答案作りとは、自分と読み手のあいだに小さいながらも数学の世界を築く作業です（抽象的な言い方ですが、数学的に正しい主張とは、常に完結した、バランスの取れた小宇宙です）。

自分の知性と読み手の知性、双方を信頼し、両者の思考をつなぎ、そこに確固たる数学的結論を創造する。この営みは、多くの中高生が考えているより、ずっとやりがいのあるものです。

この本を手に取られたあなたが、この本を通じて答案作成の方法を知り、そのたのしみに触れていただけることを祈ります。

それでは、《伝える》レッスンをはじめましょう！（まえがきより）