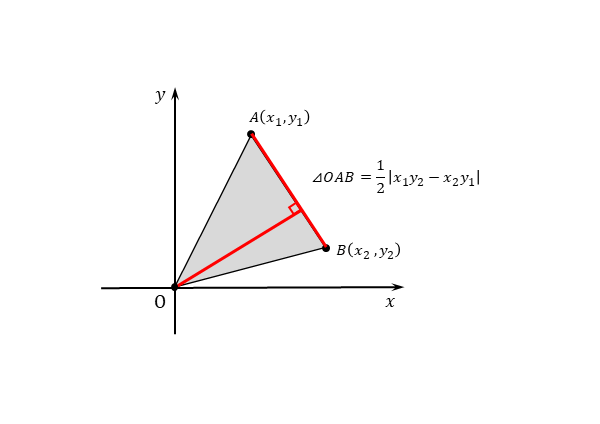図形と方程式|三角形の面積について

今回は、三角形の面積について学習しましょう。新しい事柄を学習するだけでなく、これまでに学習した事柄も総動員しなければなりません。
点の座標や直線の方程式などをすぐに求めることができるでしょうか。また、図形を扱うので、作図できないと難易度が上がります。例題や練習問題を通じて訓練しましょう。
三角形の面積
座標平面上において、三角形の面積を考えるとき、一般に3点の座標が与えられます。3つの点は三角形の頂点となる点です。
また、三角形の面積を求めるには、公式から分かるように底辺の長さと高さを必要とします。底辺の長さは2点間の距離に等しいので、公式を用いて簡単に求めることができます。
それに対して、高さは、頂点から底辺に下した垂線の長さです。高さを求めようとすると、これまでなら次の手順で求めなければなりません。
高さを求める手順
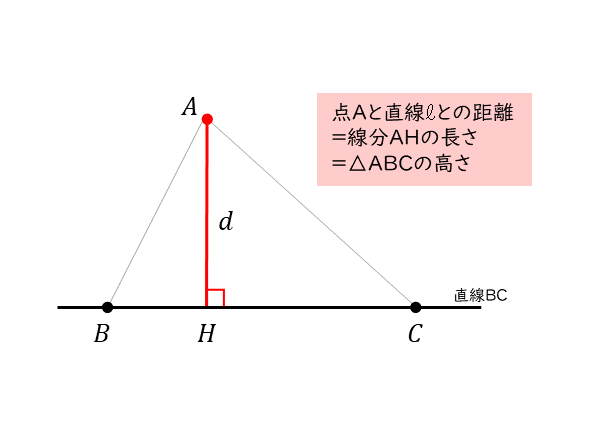
△ABCの辺BCを底辺、頂点Aから辺BCに下した垂線の足をHとする。
- 2点B,Cを通る直線の方程式を求める。
- この直線と垂直で、頂点Aを通る直線の方程式を求める。
- 2直線の交点、すなわち点Hの座標を求める。
- 線分AHの長さを2点間の距離の公式で求めて、高さとする。
このような手順で高さを求めることはできますが、手続きが多すぎて面倒です。
点と直線の距離
先ほどの△ABCで言えば、高さとなる線分AHの長さは、頂点Aと直線BCとの距離に相当します。座標平面上において、点と直線の距離が分かることはとても便利です。
一般に、点と直線の距離は以下のように表されます。
点と直線の距離
点 $(x_{1} \ , \ y_{1})$ と直線 $ax+by+c=0$ の距離 $d$ は
\begin{align*} \quad d=\frac{| ax_{1}+by_{1}+c |}{\sqrt{a^{2}+b^{2}}} \end{align*}点と直線の距離を導いてみましょう。上図の△ABCを利用します。
ただし、直線BCは、x軸やy軸に垂直な直線でない場合とします。軸に垂直な直線であれば、点と直線の距離の公式を用いる必要がないからです。
点Aと直線BCの距離dは、以下のように2点B,C間の距離(①式)で表されます。この①式から、点Hのx座標αとy座標βを消去することを目指します。
その際、傾きによる垂直条件や直線上の点であることなどを利用します。
点と直線の距離の導出
$2$ 点 $A \ , \ H$ の座標をそれぞれ
\begin{align*} \quad A(x_{1} \ , \ y_{1}) \ , \ H(\alpha \ , \ \beta) \end{align*}とする。
また、直線 $BC$ の方程式を
\begin{align*} \quad ax+by+c=0 \quad (a \neq 0 \ , \ b \neq 0) \end{align*}とする。
このとき、点 $A$ と直線 $BC$ の距離 $d$ は
\begin{align*} \quad d^{2}=AH^{2}=\left(\alpha-x_{1} \right)^{2}+\left(\beta-y_{1} \right)^{2} \quad \cdots \text{①} \end{align*}点 $H$ は直線 $BC$ 上にあるので
\begin{align*} \quad a \alpha+b \beta+c=0 \quad \cdots \text{②} \end{align*}直線 $AH$ は直線 $BC$ に垂直であるので
\begin{align*} \quad \frac{\beta-y_{1}}{\alpha-x_{1}} \cdot \left( -\frac{a}{b} \right) = -1 \end{align*}よって
\begin{align*} \quad \frac{\beta-y_{1}}{\alpha-x_{1}} = \frac{b}{a} \end{align*}さらに変形して
\begin{align*} \quad \frac{\alpha-x_{1}}{a} = \frac{\beta-y_{1}}{b}=k \end{align*}とおくと
\begin{align*} \quad \alpha=x_{1}+ak \ , \ \beta=y_{1}+bk \quad \cdots \text{③} \end{align*}③を②に代入して
\begin{align*} \quad a \left(x_{1}+ak \right)+b \left(y_{1}+bk \right)+c=0 \end{align*}$k$ について解くと
\begin{align*} \quad k=-\frac{ax_{1}+by_{1}+c}{a^{2}+b^{2}} \quad \cdots \text{④} \end{align*}また、③を①に代入して
\begin{align*} \quad d^{2}=\left(a^{2}+b^{2} \right)k^{2} \quad \cdots \text{⑤} \end{align*}よって、④を⑤に代入して
\begin{align*} \quad d^{2}=\left(a^{2}+b^{2} \right) \cdot \left(-\frac{ax_{1}+by_{1}+c}{a^{2}+b^{2}} \right)^{2} \end{align*}整理すると
\begin{align*} \quad d^{2}= \frac{(ax_{1}+by_{1}+c)^{2}}{a^{2}+b^{2}} \end{align*}$d \gt 0$ より
\begin{align*} \quad d=\frac{| ax_{1}+by_{1}+c |}{\sqrt{a^{2}+b^{2}}} \end{align*}分数の等式が得られたときは、③式のように分数を1つの文字に置き換えると扱いやすくなります。すでに学習済みの比例式の考えを利用しています。
点と直線の距離の式を利用すれば、三角形の高さを簡単に求めることができるようになります。
座標平面における図形の高さを求める場合、点と直線の距離を利用しよう。
三角形の面積を求めてみよう
三角形の面積を求めてみましょう。
例題
次の $3$ 点
\begin{align*} \quad A(1 \ , \ 1) \ , \ B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}について、次のものを求めよ。
$(1) \quad$ 直線 $BC$ の方程式
$(2) \quad$ 線分 $BC$ の長さ
$(3) \quad$ 点 $A$ と直線 $BC$ の距離
$(4) \quad$ $\triangle {ABC}$ の面積
入試レベルだと、小問形式になっておらず、いきなり△ABCの面積を求める問題もあります。そんな場合でも、例題(1)~(3)の情報が必要になります。
例題(1)の解答・解説
例題(1)
次の $3$ 点
\begin{align*} \quad A(1 \ , \ 1) \ , \ B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}について、次のものを求めよ。
直線 $BC$ の方程式
直線BCの方程式を求めるには、2点B,Cの座標を利用します。2点を通る直線の方程式に座標を代入します。
例題(1)の解答例
直線 $BC$ は $2$ 点
\begin{align*} \quad B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}を通るので
\begin{align*} &\quad \left(2-5 \right)\left(x-3 \right)-\left( 5-3 \right)\left(y-5 \right)=0 \\[ 7pt ] &\quad -3\left(x-3 \right)-2\left(y-5 \right)=0 \end{align*}よって
\begin{align*} \quad 3x+2y-19=0 \end{align*}以下の式を用いて直線BCの方程式を求めています。
2点を通る直線の方程式
異なる $2$ 点
\begin{align*} \quad (x_{1} \ , \ y_{1}) \ , \ (x_{2} \ , \ y_{2}) \end{align*}を通る直線の方程式は
\begin{align*} \quad \left(y_{2}-y_{1} \right) \left(x-x_{1} \right)-\left(x_{2}-x_{1} \right) \left(y-y_{1} \right)=0 \end{align*}2点B,Cの座標から、直線BCはx軸に垂直な直線ではないので、以下の解答例でも問題ありません。
例題(1)の別解例
直線 $BC$ は $2$ 点
\begin{align*} \quad B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}を通るので
\begin{align*} \quad y-5=\frac{2-5}{5-3} \left(x-3 \right) \end{align*}よって
\begin{align*} \quad 3x+2y-19=0 \end{align*}図示した直線に方程式を追記しておきましょう。
例題(2)の解答・解説
例題(2)
次の $3$ 点
\begin{align*} \quad A(1 \ , \ 1) \ , \ B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}について、次のものを求めよ。
線分 $BC$ の長さ
線分BCの長さは、2点B,C間の距離に等しいことに注目します。2点間の距離の式に代入します。
例題(2)の解答例
線分 $BC$ の長さは $2$ 点
\begin{align*} \quad B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}間の距離に等しいので
\begin{align*} \quad BC &= \sqrt{\left(5-3 \right)^{2}+\left(2-5 \right)^{2}} \\[ 7pt ] &= \sqrt{4+9} \end{align*}$BC \gt 0$ より
\begin{align*} \quad BC=\sqrt{13} \end{align*}以下の式を用いて2点B,C間の距離を求めています。
平面上の2点間の距離
座標平面上の $2$ 点
\begin{align*} \quad A(x_{1},y_{1}) \ , \ B(x_{2},y_{2}) \end{align*}間の距離 $AB$ は
\begin{align*} \quad AB=\sqrt{\left(x_{2}-x_{1} \right)^{2}+\left(y_{2}-y_{1} \right)^{2}} \end{align*}例題(3)の解答・解説
例題(3)
次の $3$ 点
\begin{align*} \quad A(1 \ , \ 1) \ , \ B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}について、次のものを求めよ。
点 $A$ と直線 $BC$ の距離
先ほど紹介した、点と直線の距離の式を利用します。
例題(3)の解答例
点 $A$ と直線 $BC$ の距離を $d$ とすると
\begin{align*} \quad d &= \frac{| 3 \cdot 1+2 \cdot 1-19 |}{\sqrt{ 3^{2}+2^{2}} } \\[ 7pt ] &= \frac{| -14 |}{\sqrt{9+4}} \end{align*}よって
\begin{align*} \quad d=\frac{14}{\sqrt{13}} \end{align*}これは点 $A$ から $BC$ に下した垂線の長さに等しい。
点Aと直線BCの距離が、辺BCを底辺としたときの△ABCの高さに等しいことに注意しましょう。
点と直線の距離
点 $(x_{1} \ , \ y_{1})$ と直線 $ax+by+c=0$ の距離 $d$ は
\begin{align*} \quad d=\frac{| ax_{1}+by_{1}+c |}{\sqrt{a^{2}+b^{2}}} \end{align*}例題(4)の解答・解説
例題(4)
次の $3$ 点
\begin{align*} \quad A(1 \ , \ 1) \ , \ B(3 \ , \ 5) \ , \ C(5 \ , \ 2) \end{align*}について、次のものを求めよ。
$\triangle {ABC}$ の面積
例題(1)~(3)までを順に解いていくことで必要な情報が得られます。三角形の面積の公式に代入します。
例題(4)の解答例
$\triangle {ABC}$ の面積は
\begin{align*} \quad \triangle ABC=\frac{1}{2} \cdot BC \cdot d \end{align*}$(2) \ , \ (3)$ から
\begin{align*} \quad \triangle ABC=\frac{1}{2} \cdot \sqrt{13} \cdot \frac{14}{\sqrt{13}} \end{align*}よって
\begin{align*} \quad \triangle ABC=7 \end{align*}例題(1)~(3)で必要な情報を揃えることができれば、例題(4)については問題なく解けるでしょう。
頂点の座標を用いた三角形の面積の公式
実は、三角形の3つの頂点の座標だけで三角形の面積を求めることができます。面積だけを求める問題であれば、かなり時間短縮できます。
三角形の頂点のうち1つが原点である場合、三角形の面積は、以下の式で表されます。
三角形の面積
次の $3$ 点
\begin{align*} \quad O(0 \ , \ 0) \ , \ A(x_{1} \ , \ y_{1}) \ , \ B(x_{2} \ , \ y_{2}) \end{align*}を頂点とする三角形の面積 $S$ は
\begin{align*} \quad S=\frac{1}{2}| x_{1} y_{2}-x_{2} y_{1}| \end{align*}この式を導出してみましょう。
三角形の面積の導出
原点 $O$ から直線 $AB$ に下した垂線の足を $H$ とする。
直線 $AB$ の方程式は
\begin{align*} \quad \left(y_{2}-y_{1} \right) \left(x-x_{1} \right)-\left(x_{2}-x_{1} \right) \left(y-y_{1} \right)=0 \end{align*}整理すると
\begin{align*} \quad \left(y_{2}-y_{1} \right)x-\left(x_{2}-x_{1} \right)y+x_{2} y_{1}-x_{1} y_{2}=0 \end{align*}$O(0 \ , \ 0)$ と直線 $AB$ との距離 $OH$ は
\begin{align*} \quad OH=\frac{| x_{2} y_{1}-x_{1} y_{2} |}{\sqrt{ ( y_{2}-y_{1} )^{2}+( x_{2}-x_{1} )^{2}} } \end{align*}ここで
\begin{align*} &\quad | x_{2} y_{1}-x_{1} y_{2} |=| x_{1} y_{2}-x_{2} y_{1} | \\[ 7pt ] &\quad AB=\sqrt{ ( y_{2}-y_{1} )^{2}+( x_{2}-x_{1} )^{2} } \end{align*}であるので
\begin{align*} \quad OH=\frac{| x_{1} y_{2}-x_{2} y_{1} |}{AB} \end{align*}よって、三角形の面積 $S$ は
\begin{align*} \quad S=\frac{1}{2} \cdot AB \cdot OH \end{align*}より
\begin{align*} \quad S=\frac{1}{2} \cdot AB \cdot \frac{| x_{1} y_{2}-x_{2} y_{1} |}{AB} \end{align*}したがって
\begin{align*} \quad S=\frac{1}{2}| x_{1} y_{2}-x_{2} y_{1}| \end{align*}三角形の頂点の1つが必ず原点であることが条件です。原点が頂点でない場合、三角形を平行移動して頂点が原点と重なるようにします。
頂点の座標だけで三角形の面積を求めるには、頂点の1つが必ず原点であることが条件
例題(4)の別解例
三角形の面積の公式を利用すれば、例題(4)を単独で解くことができます。ただし、頂点の1つが原点に重なるように、三角形を平行移動しましょう。
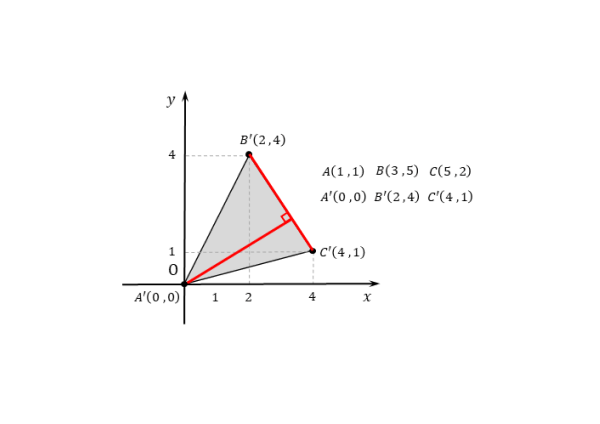
頂点の座標が変わるので注意しましょう。点Aが原点に重なるように△ABCを平行移動させます。このとき、2点B,Cはそれぞれx軸方向に-1、y軸方向に-1だけ平行移動します。
例題(4)の別解例
点 $A(1 \ , \ 1)$ が原点 $O(0 \ , \ 0)$ に重なるように$\triangle {ABC}$ を平行移動させると
\begin{align*} \quad (3-1 \ , \ 5-1) \ , \ (5-1 \ , \ 2-1) \end{align*}より、$2$ 点 $B \ , \ C$ はそれぞれ
\begin{align*} \quad B'(2 \ , \ 4) \ , \ C'(4 \ , \ 1) \end{align*}に平行移動する。
このとき
\begin{align*} \quad \triangle ABC=\triangle {OB’C’} \end{align*}であるので、$\triangle {ABC}$ の面積は
\begin{align*} \quad \triangle ABC &= \frac{1}{2}| 2 \cdot 1-4 \cdot 4| \\[ 7pt ] &= \frac{1}{2} \cdot 14 \end{align*}よって
\begin{align*} \quad \triangle ABC=7 \end{align*}頂点の平行移動をミスしなければ、とても簡単に三角形の面積を求めることができます。この式はベクトルの単元でも出てくるので、ここで覚えておきましょう。
次は、三角形の面積を扱った問題を実際に解いてみましょう。