場合の数|順列について

順列を扱った問題を解いてみよう
次の問題を考えてみましょう。
問1の解答・解説
問1
次の値を求めよ。
\begin{align*} (i) \quad {}_3 \mathrm{ P }_3 \\[ 7pt ] (ii) \quad {}_7 \mathrm{ P }_3 \end{align*}問1は、記号化された順列の総数を計算する問題です。記号Pの意味を理解していれば、正しく計算式に書き換えることができます。
公式や定理を覚えても使いこなせないのは、その式の意味をことばで理解していないからです。そうならないように記号の意味をしっかり読み取り、ことばに置き換える習慣を付けましょう。問1のような基本的な問題は訓練に最適です。
3P3は「異なる3個すべてを並べるときの順列の総数」を表しています。ですから、階乗の式で求めることができます。
また、7P3は「異なる7個の中から3個を取って並べるときの順列の総数」を表しています。ですから、nPrの式で求めることができます。
問1の解答例
\begin{align*} \quad {}_3 \mathrm{ P }_3 &= 3! \\[ 7pt ] &= 3 \cdot 2 \cdot 1 \\[ 7pt ] &= 6 \end{align*}また、$7-3+1 = 5$ より
\begin{align*} \quad {}_7 \mathrm{ P }_3 &= 7 \cdot 6 \cdot 5 \\[ 7pt ] &= 210 \end{align*}問1のポイントと解答例は以下のようになります。
注意したいのは問1(ii)です。7から3までの整数の積ではないことに注意しましょう。7-3+1=5であるので、7から5までの整数の積です。
順列の総数の式をもっと上手に使うためのコツ
nPrの式を使うとき、よく間違えるのが最後の数です。この最後の数を間違えないコツがあります。
順列の総数
異なる $n$ 個から $r$ 個を並べるときの順列の総数は
\begin{align*} \quad {}_n \mathrm{ P }_r = n \cdot (n-1) \cdot (n-2) \cdot \cdots \cdot (n-r+1) \end{align*}nPrはnからn-r+1までの整数の積で表されます。このとき、掛けられる整数の個数は、n-(n-r+1)=r個です。このことから、nから順に1ずつ減らしたr個の整数を掛ければ良いことが分かります。
7P3であれば、7を先頭にして3個の整数の積になります。7から順に1ずつ減らした整数6,5を掛けると、3個の整数の積になります。
この規則性を知っていれば、最後の数を間違うことも減らせるでしょう。上手に使って下さい。
nPrはnを先頭にしてr個の整数の積で表される。記号Pの右下の添え字rは、並べる数の個数に等しい。
問2の解答・解説
問2
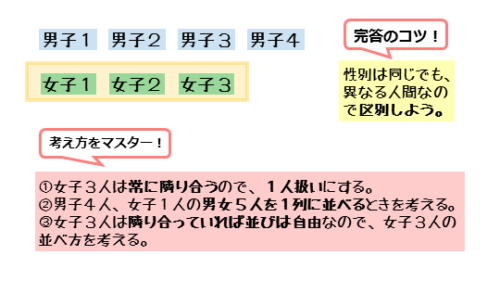
男子 $4$ 人、女子 $3$ 人が $1$ 列に並ぶとき、女子 $3$ 人が隣り合う並べ方は何通りあるか。
問2は、「1列に並ぶ」とあるので順列の総数を求める問題です。ただし、注意したいのは「女子3人が隣り合う」という条件です。
女子3人が隣り合うためには、女子3人を個別に扱わず、まとめて扱う必要があります。女子3人を1人と見なしてしまえば、女子3人がどこに並んでもつねに隣り合うことになります。これが1つ目のポイントです。
隣り合うときはひとまとめにして扱おう。
女子3人を1人と見なすと、男女5人が1列に並ぶときの順列になります。5人全員を並べるので、その総数は5!通り(または5P5通り)あります。
これで終わりではありません。次に考えることは女子3人の並び方です。
女子3人を1人扱いしましたが、3人の並び方まで考えていません。女子3人は隣り合っていれば、どんな並び方でも良いはずです。
それを踏まえると、女子3人の順列の総数は3!通り(または3P3通り)あります。ここが2つ目のポイントです。
「隣り合う」条件があるときのポイント
- 隣り合う3人を1人と見なす
- 1人扱いした3人の並べ方を考える
以上のことから、男女の並び方5!通りのそれぞれについて、女子3人の並び方が3!通りずつあることが分かります。これより積の法則で並べ方の総数を求めることができます。
問2の解答例
女子 $3$ 人を $1$ 人とみなしたとき、男女 $5$ 人が $1$ 列に並ぶときの順列の総数は ${}_5 \mathrm{ P }_5$ 通り。
男女 $5$ 人の並べ方のそれぞれについて、女子 $3$ 人の並べ方は ${}_3 \mathrm{ P }_3$ 通りずつある。
積の法則から
\begin{align*} \quad {}_5 \mathrm{ P }_5 \times {}_3 \mathrm{ P }_3 &= 5! \times 3! \\[ 7pt ] &= ( 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 ) \times ( 3 \cdot 2 \cdot 1 ) \\[ 7pt ] &= 120 \times 6 \\[ 7pt ] &= 720 \end{align*}問2のポイントと解答例は以下のようになります。
問2のような問題を解くと、樹形図を書くことや、数え上げの方法を考えることが先だと言った意味を分かってもらえるかと思います。
計算は簡単な整数の四則計算ばかりなので、樹形図を書くことや解答の方針を考えることを優先しましょう。
そして解答の方針が決まったら、簡潔に記述するために階乗やnPrを使いましょう。実際に計算するときは整数の積に書き変えますが、記述では読みやすさも大事なので上手に使いましょう。
Recommended books
単元ごとに得意・不得意がある場合、短期間で学習できる教材があると便利です。
オススメその1
1冊目は『これならわかる! 図解 場合の数と確率』です。
図が豊富で丁寧に解説されています。また、問題も多く扱っているので、演習不足にならないでしょう。
重複なく、漏れがないように数えるための考え方、数え方の基本をマスターできる教材です。
以下、2冊は短期間で学習するのに適した問題集です。場合の数や確率について一通り学習した後に取り組むと良いでしょう。
オススメその2
2冊目は『SPEED攻略10日間 数学 場合の数と確率』です。
Z会の教材は難しいというイメージがありますが、この教材は基本レベルから扱っているので、安心して取り組めます。
例題・類題・入試問題を繰り返し演習する構成になっており、典型問題の考え方や解き方を理解し、身につけることができます。
オススメその2
3冊目は『大学入試10日で極める 場合の数と確率』です。
どちらかと言えば、理系向けの教材です。短期間で、基礎から難関大突破レベルまで効率的に学習できます。
主要大学の入試において、近年出題率の高い分野の問題が掲載されているのもポイントです。また、補充問題も充実しているので、これ1冊で演習量もカバーできます。
さいごに、もう一度、頭の中を整理しよう
- 順列は、いくつかの人や物を1列に並べること、または並べたもの。
- 順列の総数は、積の法則より整数の積で表される。
- ある数から1までの整数の積は、階乗で表される。
- すべての人や物を並べるときの順列の総数は、階乗で求めることができる。
- 一部の人や物を並べるときの順列の総数は、記号Pを使って表される。
- nPrの式では、積の最後の整数に注意する。