中学数学|正負の数の四則混合算を解いてみよう

加減算と乗除算を学習した後は、これらが混在する四則混合算を学習します。計算問題での最終目標は、この四則混合算をこなせるようになることです。
四則混合算が解ける頃には、多項式や単項式の区別がつき、計算の優先順位もつけられるでしょう。
計算の流れを意識して、それが自然と頭の中でイメージできるようになりましょう。そして、素早く丁寧に計算できるように仕上げましょう。
四則の混じった計算
四則が混ざった計算を四則混合算などと言います。
四則とは、加法(加算)・減法(減算)・乗法(乗算)・除法(除算)の4種類の計算のことです。混合算なので、4種類すべてとは限りませんが、それらが1つの式の中に混じっています。
この四則混合算では、計算の優先順位があります。優先順位に従って計算しないと、正しい解を得ることはできません。
四則の優先順位
四則の優先順位は、原則的には以下のようになっています。
四則の優先順位
- 乗算や除算などの乗除算
- 加算や減算などの加減算
原則としての優先順位はありますが、カッコを含む場合にはカッコ内の計算を優先するので注意が必要です。
ただし、カッコ内に限って見れば、計算の優先順位は原則通りに加減算よりも乗除算が優先されます。算数でも数学でも計算の優先順位に違いはありません。
単項式と多項式を区別しよう
正負の数を扱うようになると、計算の優先順位は知っていても頻繁に計算ミスを起こします。
その原因を考えてみると、単項式と多項式を区別できていないことが影響しているかもしれません。
単項式と多項式の区別がつかないということは、プラス(+)やマイナス(-)が、計算記号と符号のどちらに用いられているのかを区別できていないということです。
単項式と多項式を区別できれば、それらの成り立ちから計算の優先順位が分かってきます。
四則混合算にはこれまでに学習したことが全て入っているので、その総決算のような計算です。文字を含む整式を手足のように扱うためにも演習を数多くこなすことが大切です。
正負の数の四則混合算を解いてみよう
次の計算問題を考えてみましょう。
問
次の計算をせよ。
\begin{align*} 1. \quad &5+\left(-2 \right) \times 4 \\[ 7pt ] 2. \quad &\left(-12-20 \right) \div 4 \\[ 7pt ] 3. \quad &45 \div \left(-3 \right)^2 \\[ 7pt ] 4. \quad &4 \div 7 \times \left(6-7 \right) \end{align*}式を観察すると、問1~4のすべてに乗算や除算の計算記号があることから、乗除算が含まれていることに気づきます。
また、「-」の扱いに注意したいところです。減算の計算記号なのか、それとも負の符号なのかを判断しなければなりません。
どんな計算をすれば良いか把握できたら、計算に優先順位をつけていきます。優先順位の高い計算から手をつけましょう。
優先順位の高い計算を見つけて、そこから処理していきます。このとき、計算の優先順位の高いカッコと乗除算の記号を探しましょう。
与式をよく観察しよう。そして、計算の方針を決めよう。
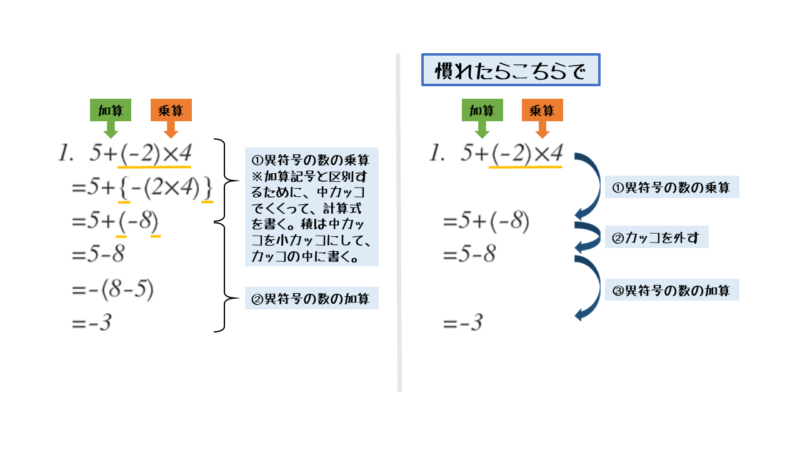
問1の解答・解説
問1
次の計算をせよ。
\begin{align*} \quad 5+\left(-2 \right) \times 4 \end{align*}単項式か多項式か
与式を左から順に見ていくと、5,+,(-2),×,4の順に並んでいます。カッコと乗算の計算記号に注目します。
カッコ内には-2があります。この-2は負の数を表しています。つまり、2についている-は負の符号を表します。このように、数についた符号を計算記号と区別するときには、その数をカッコでくくります。
たとえば、カッコがなければ+-2のような記述になります。これではどんな計算をすれば良いのか分かりません。このようなことを防ぐためにカッコを使います。
それに対して、(-2)の前にある「+」は、符号ではなく、加算を表す計算記号です。
カッコを使うと、計算記号と符号を区別できる。
加算が含まれていることから、与式は和で表される多項式と考えることができます。加算記号+の前にスラッシュを入れると、与式は2つの項からなることが分かります。
与式は多項式
数の直後にある $+$ の前にスラッシュを入れると
\begin{align*} \quad 5 \ / \ +\left(-2 \right) \times 4 \end{align*}よって、与式は $2$ つの項からなる多項式
数字の直後に+や-があれば多項式。スラッシュを入れてみよう。
単項式は多項式よりも優先順位が高い
与式が多項式だと分かりました。ここで、単項式と多項式の定義を思い出してみましょう。
単項式は積の形で表される式で、多項式は和の形で表される式でした。実際に計算するとすれば、優先順位の原則から、多項式よりも単項式の方が計算の優先順位が高くなります。
そういうわけで、複数の項(単項式)をもつ多項式の計算では、多項式全体ではなく、それぞれの項を優先して処理していけば良いことが分かります。
与式を観察した結果をまとめると、以下のようになります。
与式の観察から分かったこと
- (-2)の直前にある「+」は加算の計算記号。与式は2つの項からなる多項式。
- 1番目の項5は定数項。
- 2番目の項(-2)×4は積の形で表された項(単項式)。
分かったことをもとにして、計算の方針を立てます。
計算の方針を立てる
- 2番目の項(-2)×4の計算(乗算)
- 1番目と2番目の項を加算
計算の方針に沿って計算します。
問1の解答例
\begin{align*} \quad &5+\underline{\left(-2 \right) \times 4} \\[ 7pt ] = \ &5+\left\{-\left(2 \times 4 \right) \right\} \\[ 7pt ] = \ &5\underline{+\left(-8 \right)} \\[ 7pt ] = \ &5-8 \\[ 7pt ] = \ &-\left(8-5 \right) \\[ 7pt ] = \ &-3 \end{align*}乗算(単項式の処理)から加算(多項式の処理)へと、原則通りの優先順位で計算していることが分かります。
四則混合算では、項(単項式)から式全体(多項式)へと計算しよう。
問1のポイントと解答例をまとめると以下のようになります。
左側の方は、計算過程を丁寧に記述した解答例です。右側の方は、目標にしたい解答例です。ただし、計算過程を正しく記述できる自信がつくまでは、丁寧な記述を心掛けた方が良いでしょう。
記述が減るのは確かに楽です。しかし、記述が減ったぶんだけ話が飛躍しやすくなります。
話が飛躍しやすいので、読み手に理解されにくい記述になる可能性が高くなります。必要な文言が抜けたことが原因で減点される可能性もあります。
省略することはいつでもできますが、記述の経験がなければ必要なときに意外と記述できないものです。
日常学習では、記述形式の試験を意識して、しっかり記述する習慣を付けておいた方が良いでしょう。
カッコの使い方は結構大事
数式を記述するとき、カッコはとても便利な記号です。高校数学で使われるのは主に3種類です。
高校数学で使われるカッコは主に3種類
- 丸カッコ( )
- 波カッコ{ }
- 角カッコ[ ]
丸カッコだけでも良さそうですが、複数のカッコが重なると、どうしても見づらくなります。カッコの及ぶ範囲が分かりにくくなるからです。
そんなときは角カッコなども使うと分かりやすい数式になります。
カッコの基本的な使い方は、数や式を他と区別する使い方です。カッコでくくられた数や式を1つのかたまりとして扱うことができます。
カッコの使い方
- 数の符号と計算記号を区別する。記号や符号を連続させない。
- 特定の計算を他の計算と区別する。結果的にカッコの中の計算を優先する必要が生じる。
カッコを使うことでカッコの内と外を区別できます。
このことから、カッコの内と外の計算を区別できるようになります。その結果、カッコ内の計算は、カッコ外よりも優先順位が高くなります。
3種類のカッコの優先順位
ところで、カッコには主に3種類ありましたが、それらを一緒に使う場合、優先順位があるのでしょうか。
教科書や参考書を見ると、丸カッコ、波カッコ、角カッコの順に使われているようですが、優先順位の明確なルールはなさそうです。教科書の使い方に合わせておく方が無難でしょう。
日本では、( )(丸カッコ、小カッコ)、{ }(波カッコ、中カッコ)、[ ](角カッコ、大カッコ)のように呼んで、カッコが重なる場合は、内側から小カッコ、中カッコ、大カッコと使うように指導される。しかし、ここにもいくつか注意が必要である。
- 小( )、中{ }、大[ ]のルールは国際的ではなく、小( )、中[ ]、大{ }の順に使用する国も多いらしい。日本でも JIS 規格では「小、中、大」という呼び方はしていないそう。
- 3段以上のカッコを使う場合は、一般的にはむしろ{ }も[ ]も使わずに、単に( )のみを使うことが多い。そのためか大学の教科書などでは 2段位のカッコでも最初から( )だけしか使っていない場合も多い(これも教科書などでの説明はない)。
- 式によっては、カッコは特別な意味に用いられることがある。その場合は、その特別なカッコを他のカッコを区別して用いる必要がある。たとえば座標や集合など。
日本などの一部の国では、数式における括弧の入れ子は [{()}] の順で用いられてきた。しかし、世界的には {[()]} の順で用いられる方式が多数派である。
JIS Z 8201-1981 においても「小括弧」・「中括弧」・「大括弧」という名称は廃止され、現在は「丸括弧」・「角括弧」・「波括弧」と表記されている。
なお、この日本工業規格 (JIS) の解説文において、丸括弧・角括弧・波括弧を入れ子にする際の順序については「特に規定しない」としたうえで、{[()]} が大多数(世界中の学術誌のうち約90%)であることが付記されている。
出典 括弧 – Wikipedia 脚注より
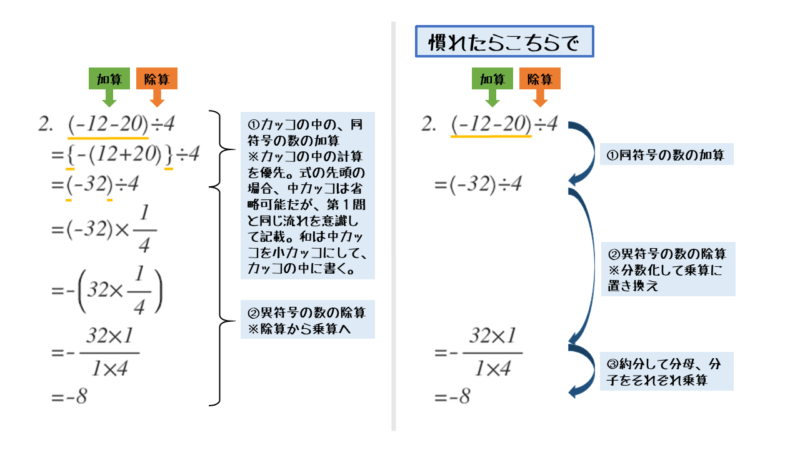
問2の解答・解説
問2
次の計算をせよ。
\begin{align*} \quad \left(-12-20 \right) \div 4 \end{align*}単項式か多項式か
与式をよく観察します。与式を左から順に見ていくと、カッコ内に-12-20があります。また、その後ろに ÷4があります。
カッコでくくられた数や式を1つのかたまりと考えると、与式は(かたまり)÷4と見なすことができます。除算は乗算に置き換えることができるので、与式全体で見れば単項式です。
また、カッコ内では、12の直後にある-の前にスラッシュを入れると、-12/-20となります。これより、カッコ内の式は-12と-20の和で表される多項式です。
与式のカッコ内は多項式
\begin{align*} \quad &-12 \ / \ -20 \\[ 7pt ] = &-12+\left(-20 \right) \end{align*}カッコ内は $-12$ と $-20$ の加算
与式全体が単項式なので、単項式の計算(乗算)を優先したいところです。しかし、カッコ内の計算の方が優先されるので、カッコ内の加算を先に処理します。
四則の優先順位に従えば、除算の方が加算よりも優先順位が高くなります。
しかし、加算をカッコでくくることによって、除算よりも先に計算することができるようになります。言い方を変えると、カッコを使えば、多項式の方を単項式よりも優先できるということです。
カッコを使うと計算の優先順位を変えることができる
与式を観察した結果をまとめると、以下のようになります。
与式の観察から分かったこと
- カッコを1つのかたまりと考えると、式全体では除算。
- カッコ内では、負の数どうしの加算。
分かったことをもとにして、計算の方針を立てます。
計算の方針を立てる
- (-12-20)の加算
- カッコ内の和と4の除算
計算の方針に沿って計算します。
問2の解答例
\begin{align*} \quad &\left(\underline{-12-20} \right) \div 4 \\[ 7pt ] = \ &\left\{-\left(12+20 \right) \right\} \div 4 \\[ 7pt ] = \ &-32 \ \underline{\div 4} \\[ 7pt ] = \ &-32 \times \frac{1}{4} \\[ 7pt ] = \ &-\left(32 \times \frac{1}{4} \right) \\[ 7pt ] = \ &-8 \end{align*}問2はカッコを使うと計算の優先順位が変わる例でした。
問2のポイントと解答例をまとめると以下のようになります。
慣れてきたら、一気に分数を作って約分する方針で解いても良いでしょう。除算を丸ごと分数にして計算する方法もあります(参考記事を参照)。
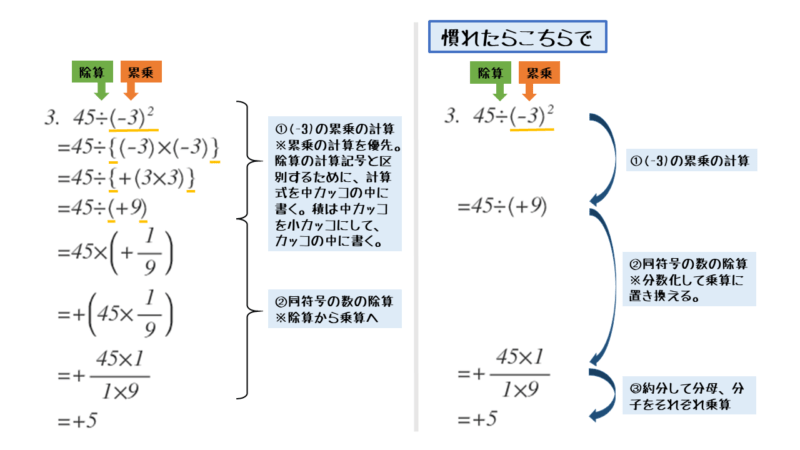
問3の解答・解説
問3
次の計算をせよ。
\begin{align*} \quad 45 \div \left(-3 \right)^{2} \end{align*}単項式か多項式か
与式を左から順に見ていくと、45,÷,(-3)2の順に並んでいます。除算の計算記号があるので、与式全体では、45 と(-3)2の除算となり、単項式と見なせます。
先に除算したいところですが、累乗は乗算を表すので、(-3)2を優先的に処理します。
なぜなら、累乗の計算は指数によって符号が変わる可能性があるからです。先に処理しておかないと、後の計算に影響を与えます。
実質的には、以下のように累乗は乗算をカッコでくくった式だと考えると分かりやすいと思います。
累乗は乗算をカッコでくくった式
\begin{align*} \quad &45 \div \left(-3 \right)^{2} \\[ 7pt ] = \ &45 \div \left\{ \left(-3 \right) \times \left(-3 \right) \right\} \end{align*}累乗を書き換えると分かりますが、波カッコ内の計算が優先される、つまり、累乗の計算が優先されるということになります。
カッコ内、累乗、乗除算、加減算の順に処理しよう。
与式を観察した結果をまとめると、以下のようになります。
与式の観察から分かったこと
- 式全体で見ると、計算記号から除算で表される単項式。
- 乗算を表す-3の累乗がある。
分かったことをもとにして、計算の方針を立てます。
計算の方針を立てる
- -3の累乗の計算
- 45と累乗結果との除算
計算の方針に沿って計算します。
問3の解答例
\begin{align*} \quad &45 \div \underline{\left(-3 \right)^{2}} \\[ 7pt ] = \ &45 \underline{\div \left(+9 \right)} \\[ 7pt ] = \ &45 \times \left(+\frac{1}{9} \right) \\[ 7pt ] = \ &+\left(45 \times \frac{1}{9} \right) \\[ 7pt ] = \ &+5 \end{align*}式全体の除算よりも累乗の計算を優先するのがポイントです。
また、与式の計算を言葉にすれば、「45を-3の累乗で除算する」です。間違っても45を -3で除算しないように気を付けましょう。
問3のポイントと解答例をまとめると以下のようになります。
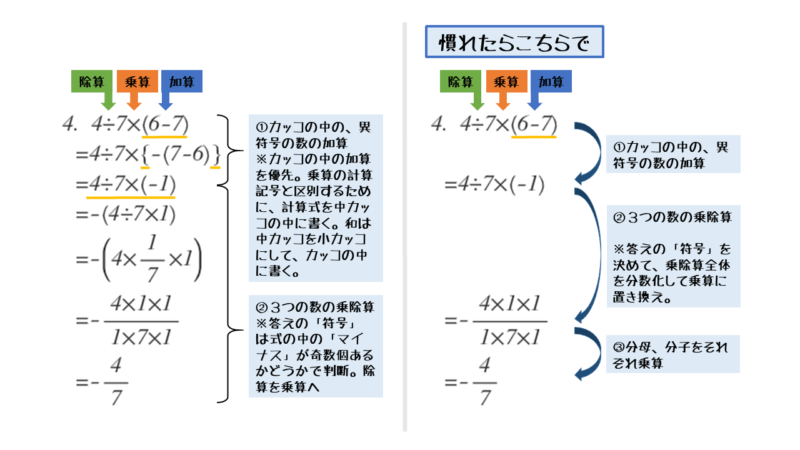
問4の解答・解説
問4
次の計算をせよ。
\begin{align*} \quad 4 \div 7 \times \left(6-7 \right) \end{align*}単項式か多項式か
与式を左から順に見ていくと、4,÷,7,×,(6-7)と並んでいます。そして、カッコ内は6-7となっています。カッコ内の数式を1つのかたまりと考えると、与式は4÷7×(かたまり)と見なせます。
与式全体では乗除算で表されるので、与式は単項式と見なせます。それに対して、カッコ内は6と-7の和で表される多項式です。
多項式よりも単項式を優先したい、つまり乗除算を優先したいところですが、カッコ内の計算を優先しなければなりません。
与式を観察した結果をまとめると、以下のようになります。
与式の観察から分かったこと
- カッコを1つのかたまりと考えると、式全体では計算記号から乗除算。
- カッコ内は、6と-7の和で表される多項式。
分かったことをもとにして、計算の方針を立てます。
計算の方針を立てる
- カッコ内(6-7)の加算
- 4,7,加算後の和の3つで乗除算
計算の方針に沿って計算します。
問4の解答例
\begin{align*} \quad &4 \div 7 \times \left(\underline{6-7} \right) \\[ 7pt ] = \ &4 \div 7 \times \left\{-\left(7-6 \right) \right\} \\[ 7pt ] = \ &4 \ \underline{\div 7} \ \times \left(-1 \right) \\[ 7pt ] = \ &4 \times \frac{1}{7} \times \left(-1 \right) \\[ 7pt ] = \ &-\left(4 \times \frac{1}{7} \times 1 \right) \\[ 7pt ] = \ &-\frac{4}{7} \end{align*}カッコ内の加算は、異符号の2数の加算です。符号と数字を分けて計算しましょう。カッコ内の加算が終わったら、乗除算です。
乗除算では、乗算に統一して計算するのが基本です。乗除算でも符号と数字を分けて計算します。
積の符号は、負の符号(-,マイナス)の個数で決まります。負の符号が奇数個あれば、積の符号は負の符号になります。正負の数が3つ以上になるとかなり便利な性質なので、覚えておきましょう。
問4のポイントと解答例をまとめると以下のようになります。
「慣れたらこちらで」のように、乗除算を1つの分数に丸ごと置き換えることもできます。これができると計算のスピードが上がります。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
オススメその1『合格る計算数学1・A・2・B』
オススメその2『鉄緑会 基礎力完成 数学Ⅰ・A+Ⅱ・B』
さいごに、もう一度まとめ
- 式をよく観察しよう。
- 単項式と多項式を区別する。
- カッコ内の計算と累乗の計算を優先する。
- 加減算(多項式)よりも乗除算(単項式)を優先する。