集合と論理｜集合と要素について

11/27/2021数学１

集合や要素を扱った問題を解いてみよう

次の問題を考えてみましょう。

問１の解答・解説

問１

$12$ の正の約数の集合を $A$ とする。次の□に適切な記号を入れよ。

\begin{align*} &(1) \quad 4 \ \text{□} \ A \\[ 7pt ] &(2) \quad 8 \ \text{□} \ A \end{align*}

問１は、集合と要素の関係を記号を使って表す問題です。基礎レベルの問題ですが、これがセンター試験で出題されました。

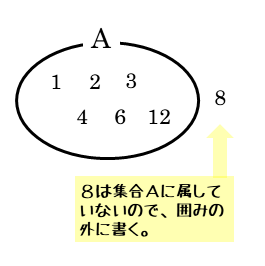
１２の正の約数を求めて、要素を書き並べる方法で集合Ａを表します。また、合わせてベン図も描いておくと良いでしょう。

問１の解答例 1⃣

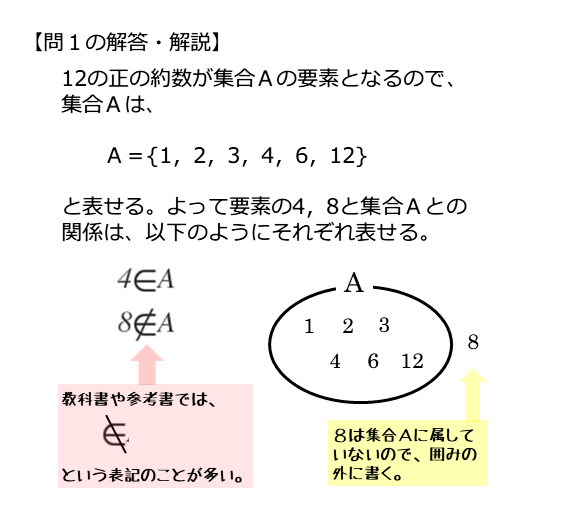
集合 $A$ の要素は $12$ の正の約数なので

\begin{align*} \quad A = \left\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 12 \right\} \end{align*}

書き並べた要素は、集合Ａに属します。それ以外は、集合Ａに属しません。４は集合Ａに属しますが、８は集合Ａに属しません。

問１の解答例 2⃣

\begin{align*} \quad &\vdots \\[ 7pt ] \quad A &= \left\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 12 \right\} \end{align*}

よって

\begin{align*} &\quad 4 \ \in \ A \\[ 7pt ] &\quad 8 \ \notin \ A \end{align*}

問１のポイントと解答例をまとめると以下のようになります。

次の問題を考えてみましょう。

問２の解答・解説

問２

$A=\{2 \ , \ 4 \ , \ 6 \ , \ 8 \} \ , \ B=\{n \ | \ n \ \text{は} \ 24 \ \text{の正の約数} \}$ とする。次の□に適切な記号を入れよ。

\begin{align*} &(1) \quad A \ \text{□} \ B \\[ 7pt ] &(2) \quad A \ \text{□} \ \varnothing \end{align*}

問２は、集合どうしの関係を記号を使って表す問題です。アルファベットの大文字が使われているのもヒントになります。

集合Ｂは、要素が満たす条件で表されているので、具体的な要素が分かりません。条件をもとに集合Ｂの要素を書き並べます。

問２の解答例 1⃣

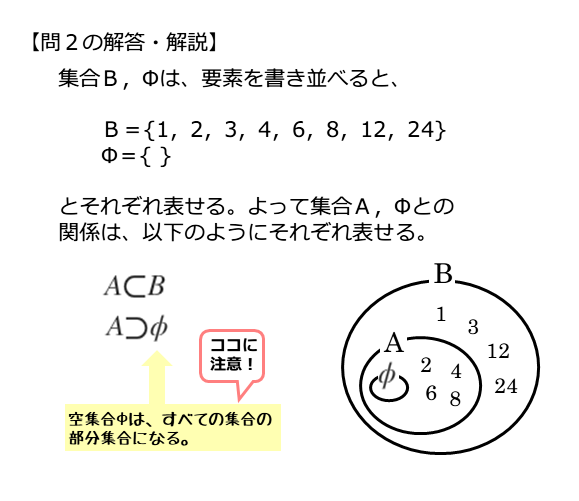
集合 $B$ の要素は、$24$ の正の約数なので

\begin{align*} \quad B = \left\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 8 \ , \ 12 \ , \ 24 \right\} \end{align*}

２つの集合Ａ，Ｂの要素を比べたり、ベン図を描いたりすると包含関係が分かります。ベン図から、集合Ａが集合Ｂの部分集合であることが分かります。

また、空集合∅はすべての集合の部分集合になるので、これは知識があれば簡単に解けます。集合と要素の関係を表す記号と間違えないように注意します。

問２の解答例 2⃣

\begin{align*} \quad &\vdots \\[ 7pt ] \quad B &= \left\{ 1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 8 \ , \ 12 \ , \ 24 \right\} \end{align*}

ここで

\begin{align*} \quad A=\left\{2 \ , \ 4 \ , \ 6 \ , \ 8 \right\} \end{align*}

より、集合 $A$ は集合 $B$ の部分集合であるので

\begin{align*} \quad A \ \subset \ B \end{align*}

また、空集合 $\varnothing$ はすべての集合の部分集合であるので

\begin{align*} \quad A \ \supset \ \varnothing \end{align*}

問２のポイントと解答例をまとめると以下のようになります。

本質を理解するために

どの科目でもそうですが、本質を理解するには、用語や記号の定義とその使い方を正しく覚えることが大切です。これらのほとんどは、各単元の導入部分で紹介されます。何事も最初が肝心です。

そして、応用レベルになると、知識があることを前提にして話が進められます。それに伴って、知識の使い方を考える問題が増えてきます。

「覚える（基礎）」から「使う（応用）」の順に進んでいるのですが、正しい知識が身に付いていなければ、間違った使い方をしてしまいます。

一見、関連がないように見える問題でも、本質的には同じ問題だったりします。そういうところが見えてくると、系統立てて覚えやすくなります。

見た目に惑わされなくなってくれば、「理解が深まっている」と解釈しても良いのではないかと思います。

相手に説明してみよう

日々の学習では、本質の理解度を把握できる学習が望まれます。そのためには「他人に説明する」というのが分かりやすい手段です。

他人に説明するには、順を追って筋道立てて（論理的に）話す必要があります。そのためには、自分が相手よりも深く理解しておく必要があります。

もし、友人たちと一緒に学習する機会があったら、ぜひ教わる側より教える側になってみて下さい。自分の理解度がはっきり分かります。

「メタ認知」を活用しよう

「メタ認知」という言葉があるそうですが、これは客観的に自分の状態を認識することだそうです。

学力の高い人は意識的かどうかにかかわらず、この「メタ認知」を習慣的に実践しているそうです。

もし、学力がなかなか向上しないようであれば、自分の理解度を客観的に判断できる学習をしているかを確認してみると良いでしょう。

自分の理解度を客観的に判断するのに最適なのは演習です。この演習を中心とした学習ができているかを考えると良いでしょう。

演習では嘘をつけません。解ける・解けないがはっきりするので、知識の定着度合いや理解度を測ることができます。

分析してすぐに手を打とう

演習したら、その結果から足りない部分を分析しましょう。そして、それをすぐに埋めていきます。

つまり、解けないことが分かったら、すぐに手を打つということです。個人的には、これが一番大切ではないかと思います。

高校での学習で一番求められるのが、分析と対策ではないでしょうか。定期試験や模試の結果に一喜一憂するのは構いませんが、そこで終わって良いのは中学までです。高校ではそこから先が求められます。

「そんなのは当たり前だ」と言われればそれまでですが、この当たり前のことを日々実践できる人は、それほど多くありません。だからこそ、たとえ大学受験のためであったとしても、高校での学習はそれなりに意味のあることなんだと思います。

「大学受験のための学習は、生きる力を養うためのものだ」と有名な予備校講師が仰ってました。その日の気分に振り回されず、自分の理解度に応じて学習するようにしたいところです。

Recommended books

大学進学を考えたとき、記述を重視した学習を日常的に行った方が良いでしょう。試験の難易度は、マーク形式よりも記述形式の方が高いからです。

また、記述では思考力や表現力などが必要で、それらを身に付けるのは一朝一夕には難しいことも理由の１つです。

記述の訓練は、基本的に教科書や参考書の例題を真似することから始まりますが、記号の使い分けや独特の表現などがあり、手探りで進めていくのは大変です。

そこでお勧めしたいのが以下の２冊です。記述の訓練に特化したテキストになります。

オススメその１

１冊目は『基礎からのジャンプアップノート数学記述式答案書き方ドリル』で、数学に苦手意識のある人におすすめです。

数学Ⅰ＋Ａ＋Ⅱ＋Ｂの記述力の基礎力を固めるなら、まずはこのドリルから！！

問題編６４ページ、別冊解答編３２ページ

証明問題、場合分けの答案の書き方のコツがわかる

「なぞって理解する」書き込みノートだから、わかりやすい答案の書き方が覚えやすい

「例（手本）」→「Check！」→「練習問題」　まねる＆繰り返すの流れで、記述力UP！

別冊「解答編」では、練習問題をくわしく解答

基礎からのジャンプアップノート数学記述式答案書き方ドリル

created by Rinker

『基礎からのジャンプアップノート』は数学以外の科目にもあります。基礎レベルの内容を扱っており、ページ数も多くありません。日常学習での予習や復習に使い勝手が良いでしょう。

オススメその２

２冊目は『総合的研究記述式答案の書き方ーー数学I・A・II・B』です。数学に苦手意識がなく、将来的に得意科目にしたい人向けです。

『総合的研究』シリーズは、チャート式やフォーカスゴールドなどと並んで有名な参考書で、数学以外の科目もあります。また、電子書籍でも出版されているので、持ち運びに苦労しないのもポイントが高いです。

この本のテーマは《伝える》ことです。私たちは、この本で、数学的に正当な思考・数学的な事実を、どうすれば文章にして他者に伝えられるか、懸命に説明しています。
ちょっとした言葉づかい、論理的な説明の順序、条件と命題の違いの意識、いろいろな文字の立場の理解・・・・・・きっと、読者の皆さんの考えを読み手に《伝える》ために、すぐ役立つはずです。
（中略）数学の答案作りとは、自分と読み手のあいだに小さいながらも数学の世界を築く作業です（抽象的な言い方ですが、数学的に正しい主張とは、常に完結した、バランスの取れた小宇宙です）。
自分の知性と読み手の知性、双方を信頼し、両者の思考をつなぎ、そこに確固たる数学的結論を創造する。この営みは、多くの中高生が考えているより、ずっとやりがいのあるものです。
この本を手に取られたあなたが、この本を通じて答案作成の方法を知り、そのたのしみに触れていただけることを祈ります。
それでは、《伝える》レッスンをはじめましょう！（まえがきより）