図形と計量|三角比の定義について

「数と式」「2次関数」と学習してきましたが、今回から図形を扱った単元「図形と計量」です。
「図形の計量」の単元で最初に学習するのは「三角比」です。「三角比」という名称から、三角形や比が話題になりそうです。
図形を扱った話なので、図形をイメージしたり、必要に応じて作図したりしながら学習しましょう。
記事の画像が見辛いときはクリックすると拡大できます。
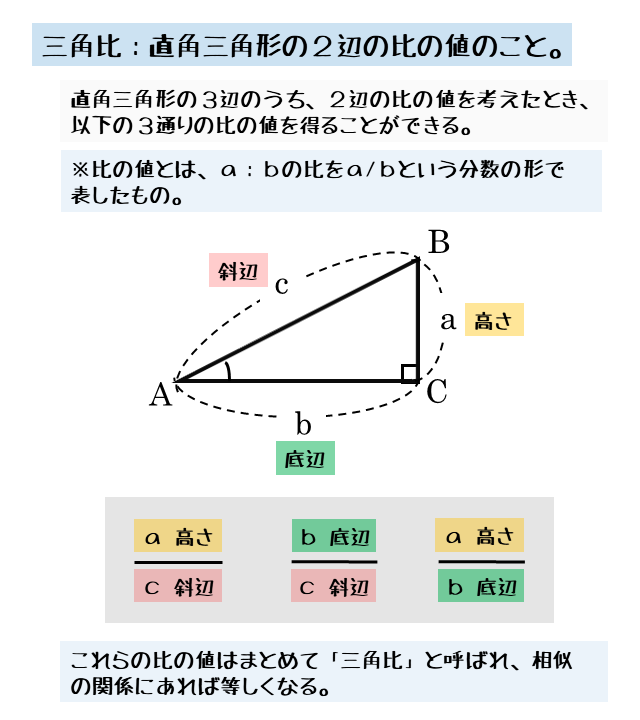
三角比は直角三角形から得られる値
三角比は、直角三角形から得られる値です。ですから、三角比を扱うとき、直角三角形をイメージしながら考えましょう。
三角比は直角三角形の2辺の関係を表す値
三角比は、具体的には直角三角形において2辺(の長さ)の比の値のことです。比の値は、中学で学習しており、2つの数量の比を分数で表したものです。
比は1:2のように表し、その比の値は1/2のように表す。また、2辺の比のことを単に辺比と言うこともある。以降、2辺の比のことを辺比と表す。
直角三角形において、2辺の選び方は3通りあるので、辺比の値は3通りあります(逆数は除く)。これら3つの辺比の値をまとめて「三角比」と言います。
2辺を選んで求めた辺比の値、つまり三角比は以下のように3通りあります。
三角比は実は中学でも使っていた
三角比は、比の値と言っていただけで、実は相似の単元で使っていました。どこで使っていたか分かるでしょうか?
相似の関係にある三角形の辺の長さを求めるとき、相似比を使って比例式を作って求めます。この計算過程で三角比が登場します。
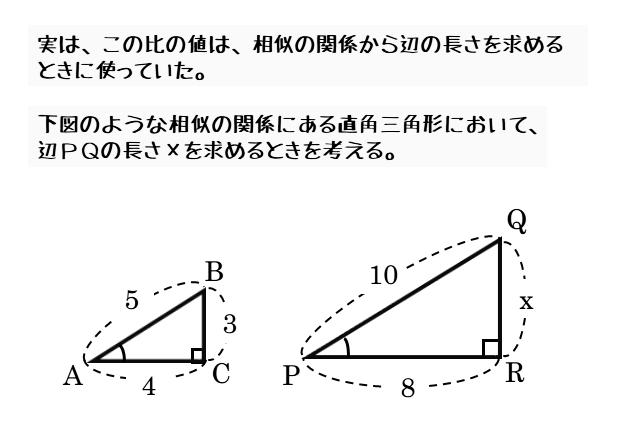
次の直角三角形の辺の長さ(高さ)を求めてみましょう。
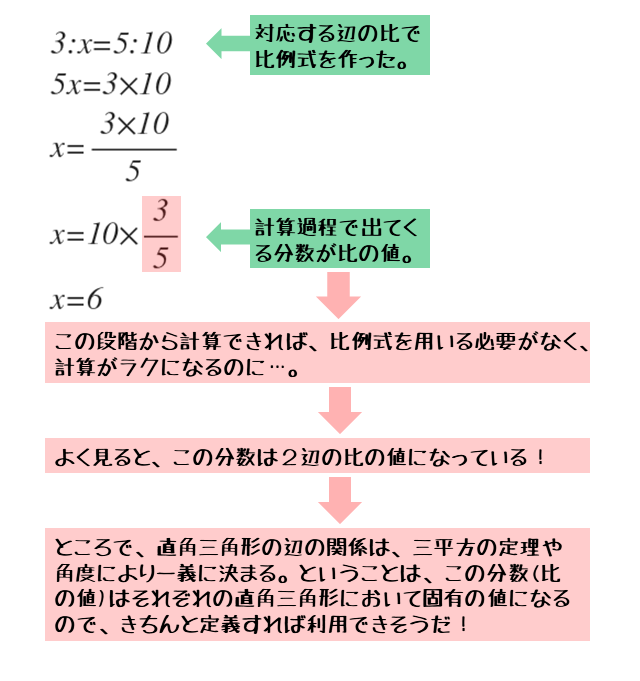
2組の辺の比から比例式を作り、内項の積と外項の積の関係から方程式を導きます。この方程式を解けば高さを求めることができます。
相似と比の値
このまま方程式を解くのであれば約分しますが、今回は三角比が分かるように約分せずに変形します。すると、斜辺と高さで得られる三角比が、計算過程に出てきます。
相似と比の値
比の値を意識することはなかったでしょうが、計算の中に比の値、つまり三角比が登場していたことは確かです。
ここから分かることは、相似の関係にある直角三角形の辺の長さは、比の値を使えば求めることができるということです。
察しの良い人なら、三角比から得られるメリットが想像できると思います。
三角比を上手に利用すれば、比例式から方程式を導出することなく、辺の長さを求めることができるようになります。過程をかなり省略することができるので、計算がラクになります。
中学では、3辺の比を使っていました。それに対して高校では、もっと計算をラクに行うために、辺比の値、つまり三角比を積極的に使っていこうということです。
1つの鋭角が決まると、三角比も決まる
直角三角形では、3つの内角のうち1つは直角(90°)です。
三角形の内角の和は180°なので、残り2つの鋭角の和は90°と分かります。このとき、一方の鋭角の大きさが決まれば、他方の鋭角の大きさも決まります。
このように1つの鋭角の大きさが決まってしまうと、直角三角形の形が決まってしまいます。直角三角形の形が決まってしまえば、3辺の長さの関係が分かるので辺比の値も決まります。
直角三角形はこのような性質をもつので、角度と辺比の値とを関数として考えることができるようになります。
角度と三角比の関係
1つの鋭角が決まれば、直角三角形の形が決まる。
⇒形が決まれば、辺の長さの関係、つまり辺比の値が決まる。
つまり
1つの鋭角が決まれば、辺比の値が決まる。
⇒辺比の値(三角比)は角度の関数。
数学2になると、「三角関数」として角度と辺比の値との関係を本格的に学習します。この単元で、角度と辺比の値の関係を結び付けて考えるようにしておきましょう。
「三角比」が、直角三角形の2辺の関係を表し、角度とも関係があることをイメージできたのではないでしょうか。
次は、相似の関係にある直角三角形において、三角比がどうなるかを考えてみます。
相似の関係にある直角三角形の三角比
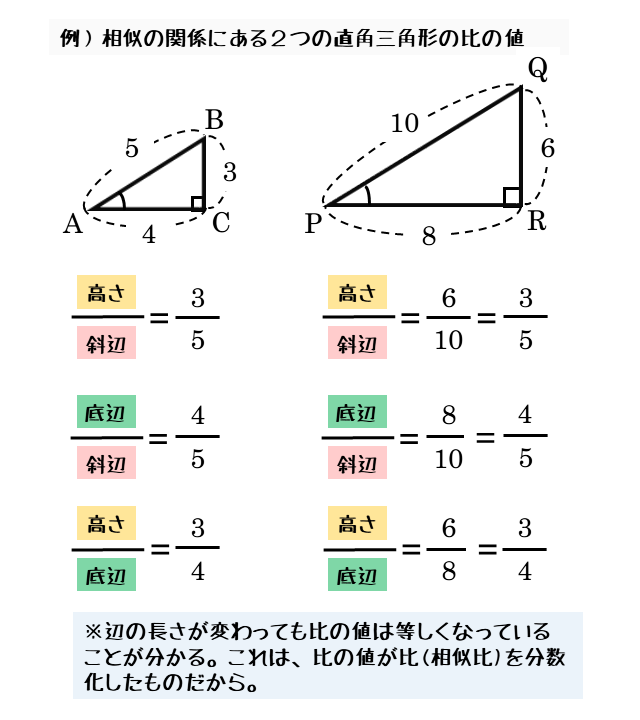
「3cm,4cm,5cmの直角三角形」と「6cm,8cm,10cmの直角三角形」を考えてみましょう。
2つの直角三角形は、どちらも3辺の比が3:4:5となる三角形なので、相似な図形です。ただし、形は同じでも大きさが異なります。
それぞれの直角三角形について、2辺を選んで辺比の値、すなわち三角比を求めてみます。すると、それぞれの値が等しくなることが分かります。
この三角比は、実際の辺の長さの代わりに3辺の比を使っても求めることができます。
3辺の比が分かっていれば、辺の長さが分からなくても三角比を求めることができる。
実際の辺の長さは、それぞれの直角三角形で異なります。しかし、三角比であれば、辺の長さにかかわらず等しくなります。これが比や比の値の良いところです。
比や比の値であれば、相似な図形であれば横断的に用いることができます。比や割合はとても便利な数量なので、ぜひ使えるようにしておきましょう。
以上のことから、相似な直角三角形であれば、三角比はつねに等しくなることが分かります。
三角比は、それぞれの直角三角形がもつ固有値と考えられる。この固有値が等しい場合、2つの直角三角形は相似の関係にあることが分かる。
三角比のことが分かったので、次は定義について学習します。