図形と計量|三角比の相互関係について その2

三角比の相互関係について学習しました。三角比の相互関係と言っても、正弦・余弦・正接の3つの関係を式で表すことでした。
今回も三角比の相互関係を学習するのですが、鋭角と鈍角に対する三角比の相互関係についてです。
作図しながら考えると意外と簡単に求めることができるので、実際に手を動かしながら考えてみると良いでしょう。
記事の画像が見辛いときはクリックすると拡大できます。
2つの角に対する三角比の相互関係について
鋭角(0°<θ<90°)に対する三角比は、すべての角に対する三角比のもとになります。そのことは三角比の拡張で学習しました。
今回の相互関係は2つの角に対する三角比の相互関係です。
2つの鋭角に対する三角比の相互関係について
2つの角の和が90°のとき
2つの角の和が90°のときを考えてみましょう。このとき、2つの角はともに鋭角になります。
一般に、2つの角について以下のようなことが言えます。
2つの角の和が90°のとき
一方の角の大きさをθとすると、他方の角の大きさは(90°-θ)と表せる。
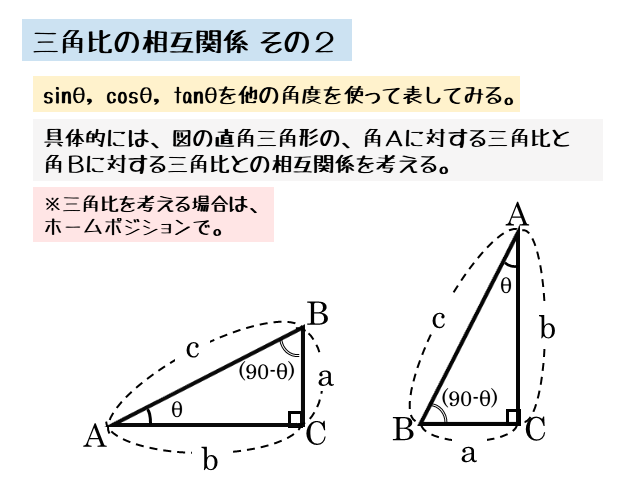
2つの角の和が90°になる図形の一例として、直角三角形があります。そこで、図のような直角三角形ABCを考えます。
直角以外の残りの2つの内角はともに鋭角であり、それらの和は90°です(ここでは簡単に角A,Bと言います)。
左図が角A、右図が角Bに注目したときの図です。
注目する角が異なると、三角比の値が異なることがあります。ですから、同じ三角形であっても向きを変えて作図した方が良いでしょう。
角Aに注目したときの三角比と、角Bに注目したときの三角比は以下の通りです。
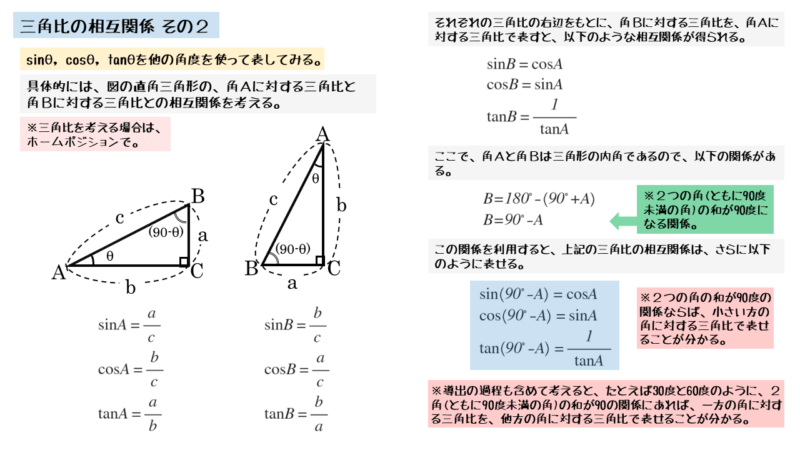
角Aに対する三角比
\begin{align*} &\quad \sin A = \frac{a}{c} \\[ 7pt ] &\quad \cos A = \frac{b}{c} \\[ 7pt ] &\quad \tan A = \frac{a}{b} \end{align*}角Bに対する三角比
\begin{align*} &\quad \sin B = \frac{b}{c} \\[ 7pt ] &\quad \cos B = \frac{a}{c} \\[ 7pt ] &\quad \tan B = \frac{b}{a} \end{align*}それぞれの三角比の右辺を見比べると、角A,Bに対する三角比の相互関係を式で表せます。
2つの角A,Bに対する三角比の相互関係
\begin{align*} &\quad \sin A = \cos B \\[ 7pt ] &\quad \cos A = \sin B \\[ 7pt ] &\quad \tan A = \frac{1}{\tan B} \end{align*}ここで、2つの角A,Bの和が90°であることから、角Aを用いて角BをB=90-Aと表せます。これを先ほどの式に代入すると以下のようになります。
一方の内角に対する三角比を他方の内角で表す
直角三角形 $ABC$ において
\begin{align*} \quad A+B=90^{\circ} \quad \cdots \text{①} \end{align*}であるとき
\begin{align*} &\quad \sin A = \cos B \\[ 7pt ] &\quad \cos A = \sin B \\[ 7pt ] &\quad \tan A = \frac{1}{\tan B} \end{align*}が成り立つ。また、①より
\begin{align*} \quad B=90^{\circ}-A \end{align*}であるので、これを $3$ つの等式の右辺に代入すると
\begin{align*} &\quad \sin A = \cos \left(90^{\circ} – A \right) \\[ 7pt ] &\quad \cos A = \sin \left(90^{\circ} – A \right) \\[ 7pt ] &\quad \tan A = \frac{1}{\tan \left(90^{\circ} – A \right)} \end{align*}両辺を入れ替えて
\begin{align*} &\quad \cos \left(90^{\circ} – A \right) = \sin A \\[ 7pt ] &\quad \sin \left(90^{\circ} – A \right) = \cos A \\[ 7pt ] &\quad \tan \left(90^{\circ} – A \right) = \frac{1}{\tan A} \end{align*}このような相互関係から分かるのは、三角形の2つの角の和が90°であれば、一方の角に対する三角比を他方の角に対する三角比で表すことができるということです。
一般に、角Aの大きさをθとすると角Bの大きさを(90°-θ)と表せるので、θを使った形が公式になっていることが多いです。
これまでをまとめると以下のようになります。
次は、鋭角と鈍角の相互関係を考えてみましょう。
鋭角と鈍角に対する三角比の相互関係について
2つの角の差が90°のとき
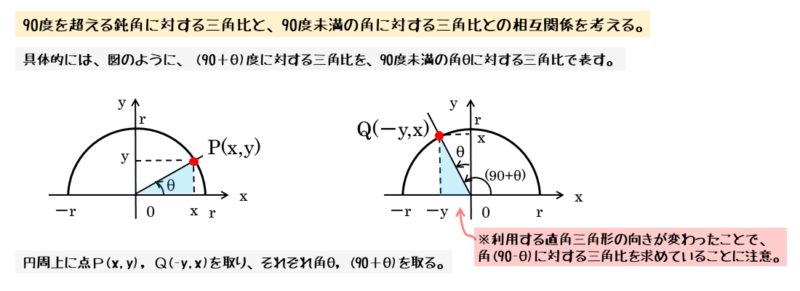
2つの角の差が90°のときを考えてみましょう。このとき、一方が鋭角になれば、他方は鈍角になります。鈍角に対する三角比を扱うので、座標平面で考えます。
一般に、2つの角について以下のようなことが言えます。
2つの角の差が90°のとき
一方の角の大きさをθとすると、他方の角の大きさは(90°+θ)と表せる。
鋭角の大きさをθとすると、2つの角の差から鈍角の大きさは(90°+θ)と表せます。このとき、鈍角を表す図から分かるように、y軸の正の部分と動径のなす角の大きさはθです。
また、鋭角のときにできる動径と円周の交点Pの座標を(x,y)とすると、鈍角のときにできる動径と円周の交点Qの座標は、合同な直角三角形(向きに注意)を上手く利用すると(-y,x)になります。
この座標と半径を利用してそれぞれの角に対する三角比を求めます。座標を利用して三角比を求めるので、符号に注意しましょう。
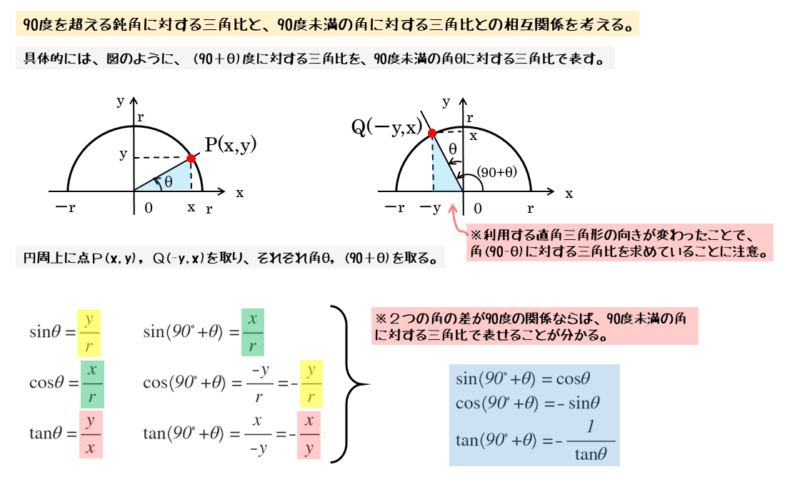
鋭角に対する三角比
半径 $r$、点 $P \ (x \ , \ y)$ より
\begin{align*} &\quad \sin \theta = \frac{y}{r} \\[ 7pt ] &\quad \cos \theta = \frac{x}{r} \\[ 7pt ] &\quad \tan \theta = \frac{y}{x} \end{align*}鈍角に対する三角比
半径 $r$、点 $Q \ (-y \ , \ x)$ より
\begin{align*} &\quad \sin \left(90^{\circ} + \theta \right) = \frac{x}{r} \\[ 7pt ] &\quad \cos \left(90^{\circ} + \theta \right) = – \frac{y}{r} \\[ 7pt ] &\quad \tan \left(90^{\circ} + \theta \right) = – \frac{x}{y} \end{align*}それぞれの三角比の右辺を見比べると、鋭角と鈍角に対する三角比の相互関係を式で表せます。
鋭角と鈍角に対する三角比の相互関係
\begin{align*} &\quad \sin \left(90^{\circ}+ \theta \right) = \cos \theta \\[ 7pt ] &\quad \cos \left(90^{\circ}+ \theta \right) = -\sin \theta \\[ 7pt ] &\quad \tan \left(90^{\circ}+ \theta \right) = -\frac{1}{\tan \theta} \end{align*}2つの角の差が90°のとき、鈍角に対する三角比を、鋭角に対する三角比で表した式が相互関係を表す式です。
これまでをまとめると以下のようになります。
この相互関係から、2つの角の差が90°のとき、90°を超える鈍角を使わず、鋭角に対する三角比を求めれば良いことが分かります。
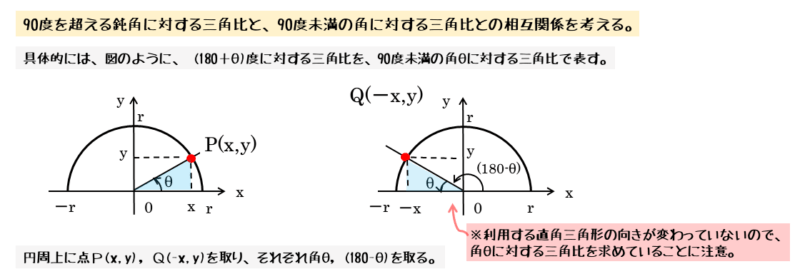
2つの角の和が180°のとき
2つの角の和が180°のときを考えてみましょう。
このとき、一方が鋭角であれば、他方は鈍角になります。鈍角に対する三角比を扱うので、先ほどと同じように座標平面で考えます。
一般に、2つの角について以下のようなことが言えます。
2つの角の和が180°のとき
一方の角の大きさをθとすると、他方の角の大きさは(180°-θ)と表せる。
鋭角の大きさをθとすると、2つの角の和から鈍角の大きさは(180°-θ)と表せます。このとき、鈍角を表す図から分かるように、x軸の負の部分と動径のなす角の大きさはθです。
また、鋭角のとき、動径と円周との交点Pの座標を(x,y)とすると、鈍角のとき、動径と円周との交点Qの座標は、合同な直角三角形を上手く利用すると(-x,y)です。
この座標と半径を利用してそれぞれの角に対する三角比を求めます。座標を利用するので符号に注意しましょう。
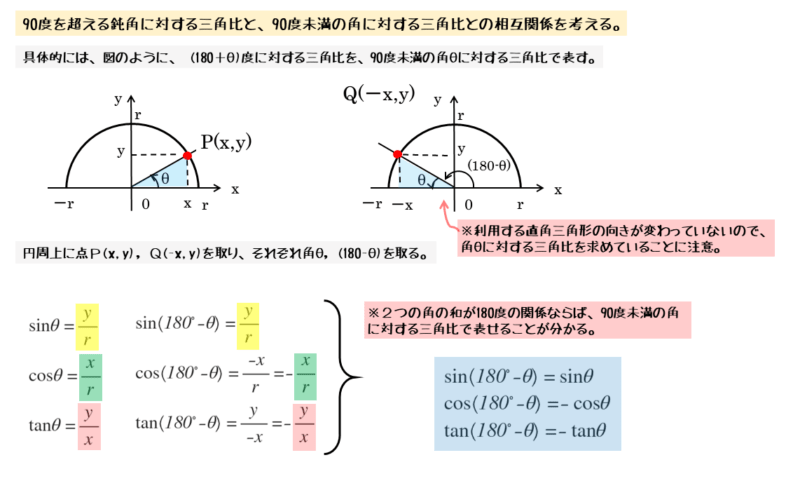
鋭角に対する三角比
半径 $r$、点 $P \ (x \ , \ y)$ より
\begin{align*} &\quad \sin \theta = \frac{y}{r} \\[ 7pt ] &\quad \cos \theta = \frac{x}{r} \\[ 7pt ] &\quad \tan \theta = \frac{y}{x} \end{align*}鈍角に対する三角比
半径 $r$、点 $Q \ (-x \ , \ y)$ より
\begin{align*} &\quad \sin \left(180^{\circ} – \theta \right) = \frac{y}{r} \\[ 7pt ] &\quad \cos \left(180^{\circ} – \theta \right) = – \frac{x}{r} \\[ 7pt ] &\quad \tan \left(180^{\circ} – \theta \right) = – \frac{y}{x} \end{align*}それぞれの三角比の右辺を見比べると、鋭角と鈍角に対する三角比の相互関係を式で表せます。
鋭角と鈍角に対する三角比の相互関係
\begin{align*} &\quad \sin \left(180^{\circ} – \theta \right) = \sin \theta \\[ 7pt ] &\quad \cos \left(180^{\circ} – \theta \right) = -\cos \theta \\[ 7pt ] &\quad \tan \left(180^{\circ} – \theta \right) = -\tan \theta \end{align*}2つの角の和が180°のとき、鈍角に対する三角比を、鋭角に対する三角比で表した式が相互関係を表す式です。
これまでをまとめると以下のようになります。
2つの角の差が90°のときと間違えやすいので作図することをお勧めします。作図すれば間違うことはないでしょう。
三角比の相互関係を利用して鋭角に対する三角比に置き換えるのがポイント
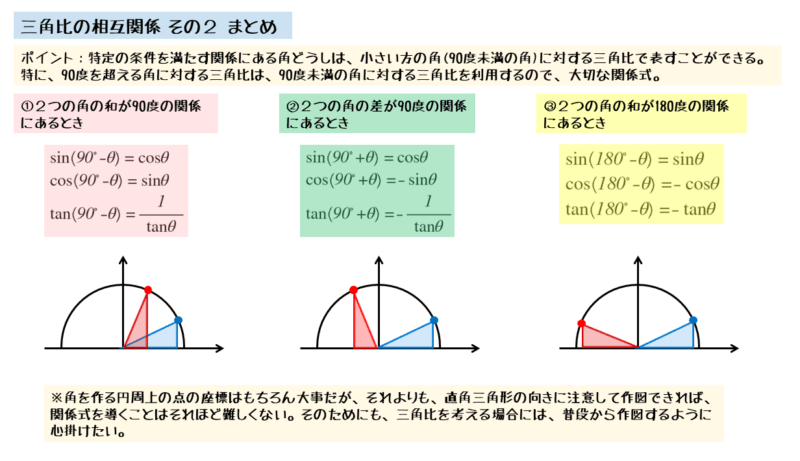
2つの角について、以下の3つの条件が成り立つときをそれぞれ考えました。
2つの角の関係3パターン
- 2つの角の和が90°のとき
- 2つの角の差が90°のとき
- 2つの角の和が180°のとき
条件は様々ですが、鈍角に対する三角比は、鋭角に対する三角比によって表されることが分かりました。
なぜこのようなことが必要かと言うと、三角比の拡張で学習したように、鈍角に対する三角比を求めると言っても、実際には鋭角に対する三角比を利用しているからです。
ですから、どの鋭角に対する三角比を利用したのかを、式でしっかり記述できた方が便利です。未知の角について考える(三角比の方程式)こともあるでしょうから、記述できることは大切です。
相互関係を表す式がたくさんあって覚えるのが大変だと思う人がいるかもしれません。しかしこれらの式は、作図さえできれば導出するのは意外と簡単です。
暗記することに一生懸命になるよりも、作図して図形的な関係を理解して導出できる方が格段に良いです。実際に手を動かして導出することをお勧めします。
作図する際のポイントは、もとにする直角三角形(鋭角θ)が、鈍角(90°+θや180°-θなど)ではどの向きに配置されるかを把握することです。把握できれば、合同な直角三角形なので点の座標も分かります。
3つの場合を一覧にまとめると以下のようになります。どのような直角三角形ができているのかを把握しましょう。
この後の単元では、三角比を使った方程式や不等式が出てきます。そのときに作図が必要になるので、今のうちに慣れておきましょう。
Recommended books
図形の問題は、気付けないと全くと言って良いほど手も足も出なくなります。気付けるかどうかはやはり日頃から作図したり、図形を色んな角度から眺めたりすることだと思います。
そのためにもやはり演習量は大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。
演習をこなすとなると、単元別になった教材を使って集中的にこなすと良いでしょう。網羅型でも良いですが、苦手意識のある単元であれば、単元別に特化した教材の方が良いかもしれません。
オススメその1
分野ごとに押さえていくのに役立つのは『高速トレーニング』シリーズです。三角関数、ベクトル、数列などの分野もあります。
ここで紹介するのは『数学1高速トレーニング 三角比編』です。
三角比に苦手意識のある人にとって、躓きやすいところを解説してあるので良い教材だと思います。基礎の定着に向いた教材です。
これで自信がついたら、チャートなどのもう少し難易度の高い問題を扱った教材に取り組むと良いでしょう。三角比は三角関数に関わるので、ここでしっかりマスターしておきましょう。
オススメその2
『改訂版 坂田アキラの三角比・平面図形が面白いほどわかる本』もおすすめです。
計算過程が省略されず、丁寧に記述されているので、計算の途中で躓くこともほとんどないでしょう。苦手な人や初学者にとって良い補助教材になると思います。
坂田のビジュアル解説で最近流行りの空間図形までフォロー!
数学1「図形と計量」(いわゆる三角比)と数学A「図形の性質」の基本事項をまとめ、それぞれの典型問題および融合問題の考え方・解き方がていねいに解説されています。
また、今回の改訂により、近年の大学入試(上位から下位まで幅広く)で頻出の空間図形の問題を厚くしました。
オススメその3
『中学入試 算数図形問題完全マスター』と『中学入試 算数図形問題完全マスター ハイレベル』は中学入試のための教材ですが、図形に苦手意識がある人にはちょうど良いかもしれません。
公立校の適性検査型入試問題を意識し、長文の問題や思考力・表現力を要する問題も収録されています。チャート式で有名な数研出版の教材なので、安心して取り組めるでしょう。
さいごに、もう一度、頭の中を整理しよう
- 鈍角に対する三角比は、鋭角に対する三角比で表すことができる。
- 鋭角と鈍角に対する三角比の相互関係は、三角比の拡張を利用して導出できる。