図形と計量|正弦定理について

今回は、正弦定理について学習しましょう。正弦定理はこの後の余弦定理とともに頻出事項です。
どのようにして導かれるのか、またどのような関係を表す定理なのかをしっかり理解しましょう。
記事の画像が見辛いときはクリックすると拡大できます。
三角比の正弦を用いた定理
正弦定理とは、その名の通り、3つある三角比のうち正弦に関する定理です。図形に関わる定理なので、作図しながら定理を確認していきましょう。
図形の基礎を確認
正弦定理を考えるにあたって、三角形を扱います。このとき、専門的な用語を使うのできちんと覚えておきましょう。
△ABCにおいて、3つの内角にはそれぞれ向かい合う辺があります。この辺を対辺と言います。
また、3つの辺から見れば、それらに向かい合う内角があるので、この内角を対角と言います。
三角形を扱うとき、一般に対辺の長さを対角の頂点に合わせて定義します。
たとえば、∠Aの対辺BCをBC=aとおきます。このようにすると、対角と対辺の対応関係が分かりやすいので、図形をイメージしやすくなります。
正弦定理に出てくる図形は三角形とその外接円
正弦定理では、三角形はもちろんですが、その三角形に外接する円が登場します。三角形や四角形などの図形に外接する円のことを外接円と言います。
外接円は、三角形や四角形に外側から接する円のこと。三角形の頂点はすべて円周上にある。三角形や四角形が円に囲われているイメージ。
三角形とその外接円との間に成り立つ定理が正弦定理ですが、三角形と言っても、直角三角形だけでなく、鋭角三角形や鈍角三角形などがあります。すべての三角形に対して成り立つ定理なのか確認してみましょう。
鋭角三角形とその外接円の場合
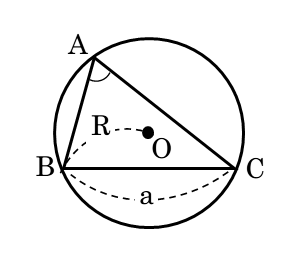
鋭角三角形である△ABCとその外接円Oを考えます。
図形の定義
$\triangle ABC$ と外接円 $O$ について、$\angle {BAC} = A \ , \ BC=a$、円 $O$ の半径を $R$ 、$\angle A$ に対する正弦を $\sin A$ とおく。
辺や半径の長さなどを定義しましたが、鋭角三角形であり、∠Aの大きさも不明なので三角比の定義を利用することができません。
直角三角形であれば、定義通り辺の長さから三角比を求めることができる。また、直角三角形以外では、角の大きさが分かっていれば、三角比の拡張から求めることができる。
このままでは正弦の値を求めることができません。そこで、円周角の性質を利用します。
頂点Aが円周上を動くと、△ABCの形が変わります。それでも同一の弧に対する円周角なので、∠Aの大きさは変わりません。
この性質を利用すると、外接円の直径を一辺とする三角形ができます。
円周角の定理 … 同一の弧に対する円周角は等しい。
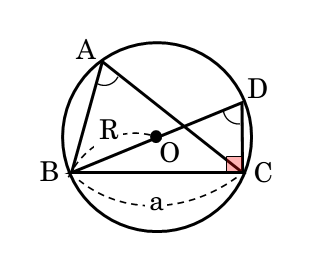
この三角形を△DBCとすると、図では∠D=∠A,BD=2R(直径),∠C=90°となる直角三角形ができます。
△DBCは直角三角形なので、三角比を辺の長さから求めることができます。
△ABCから△DBCへ
$\triangle DBC$ は直角三角形なので
\begin{align*} \quad \sin D = \frac{BC}{BD} \end{align*}$\angle D =\angle A \ , \ BC = a \ , \ BD = 2R$ より
\begin{align*} \quad \sin A = \frac{a}{2R} \end{align*}同じように円周角の性質を利用して直角三角形を作ると、∠B,∠Cに対する正弦も求めることができます。
円周角の性質を利用して直角三角形を作る
$\angle B$ の対辺 $AC$、$\angle C$ の対辺 $AB$ をそれぞれ
\begin{align*} &\quad AC=b \\[ 7pt ] &\quad AB=c \end{align*}とすると
\begin{align*} &\quad \sin B = \frac{b}{2R} \\[ 7pt ] &\quad \sin C = \frac{c}{2R} \end{align*}3つの内角について正弦の値を求めることができましたが、それぞれ2Rについて変形します。
2Rについて変形する
\begin{align*} &\quad \sin A = \frac{a}{2R} \\[ 7pt ] &\quad \sin B = \frac{b}{2R} \\[ 7pt ] &\quad \sin C = \frac{c}{2R} \end{align*}これらを $2R$ について整理すると
\begin{align*} &\quad 2R = \frac{a}{\sin A} \\[ 7pt ] &\quad 2R = \frac{b}{\sin B} \\[ 7pt ] &\quad 2R = \frac{c}{\sin C} \end{align*}すべて2Rについての式であるので、3つの等式を1つの等式でまとめて表すことができます。
3つの等式を1つの等式にまとめる
\begin{align*} &\quad 2R = \frac{a}{\sin A} \\[ 7pt ] &\quad 2R = \frac{b}{\sin B} \\[ 7pt ] &\quad 2R = \frac{c}{\sin C} \end{align*}これらを $1$ つの等式にまとめると
\begin{align*} \quad \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R \end{align*}この等式は4つの値はすべて等しいことを表しています。
便宜上、1つの等式にまとめただけで、実際は4つの値から2つを選んだ等式を使う。選び方は6通りある。
このように、鋭角三角形と外接円があるとき、正弦と外接円の半径の間には特定の関係が成り立ち、式で表せることが分かりました。これを正弦定理と言います。
そして、鋭角三角形の1つの内角に対する正弦は、対辺の長さと外接円の半径が分かれば良いということも分かりました。
式の導出自体は難しいものではありません。しかし、三角比の定義を使うためとはいえ、「円周角の性質を利用して、∠Aと等しい内角をもつ直角三角形を作る」という発想は、初見では難しいかと思います。
このような視点を身に付けるためにも公式や定理の導出に積極的に取り組んでほしいです。センター試験でも導出に関わる問題が出題されることが意外と多いのでぜひ習慣付けたいものです。
次は、鈍角三角形の場合です。
鈍角三角形とその外接円の場合
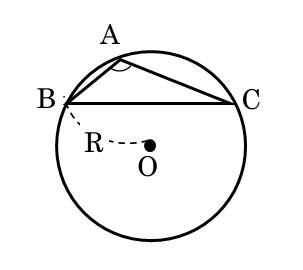
鈍角三角形である△ABCとその外接円Oを考えます。辺の長さや角の大きさなどの条件は先ほどと同じです。
図形の定義
$\triangle ABC$ と外接円 $O$ について、$\angle {BAC} = A \ , \ BC=a$、円 $O$ の半径を $R$ 、$\angle A$ に対する正弦を $\sin A$ とおく。
円周上の頂点Aを動かして直角三角形△DBCを作ります。
△BDCは直角三角形なので、三角比の定義を利用して∠Dに対する正弦を求めます。
△ABCから△DBCへ
$\triangle DBC$ は直角三角形なので
\begin{align*} \quad \sin D = \frac{BC}{BD} \end{align*}$\angle D =\angle A \ , \ BC = a \ , \ BD = 2R$ より
\begin{align*} \quad \sin A = \frac{a}{2R} \end{align*}∠Dに対する正弦を求めることはできましたが、ここで注意したいことがあります。∠Aと∠Dは大きさの等しい角でしょうか?
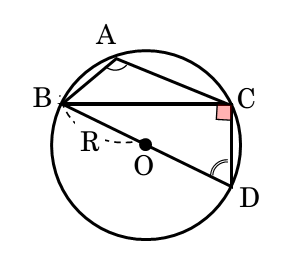
鋭角三角形のとき、同一の弧に対する円周角でしたが、鈍角三角形では異なる弧に対してできています。
∠AはAを含まない弧BCに対する円周角です。それに対して、∠DはAを含む弧BCに対する円周角です。図を見ても明らかなように、∠Aと∠Dの大きさは等しくありません。
ここで中学でも学習した中心角と円周角の性質を利用します。中心角と円周角の性質から、∠D=180°-∠Aの関係が得られます(証明は後述)。
この式を先ほどの∠Dに対する正弦に代入すると、∠Aを用いた式を導くことができます。
∠Aを用いた式を導く
\begin{align*} \quad \sin D = \frac{a}{2R} \end{align*}$\angle D = 180^{\circ} – \angle A$ より
\begin{align*} \quad \sin \left( 180^{\circ} – A \right) = \frac{a}{2R} \end{align*}∠Aに対する正弦ではなく、∠(180°-A)に対する正弦の形で導出されます。このとき、三角比の相互関係を利用すれば、∠Aに対する正弦を導くことができます。
三角比の相互関係
\begin{align*} \quad \sin \left( 180^{\circ} – A \right) = \sin A \end{align*}これを利用すると、以下のようになります。
三角比の相互関係を利用する
\begin{align*} \quad \sin \left( 180^{\circ} – A \right) = \frac{a}{2R} \end{align*}三角比の相互関係より
\begin{align*} \quad \sin A = \frac{a}{2R} \end{align*}導出の流れは多少異なりましたが、得られた関係式は同じになります。∠B,∠Cに対する正弦も同じように求めることができます。
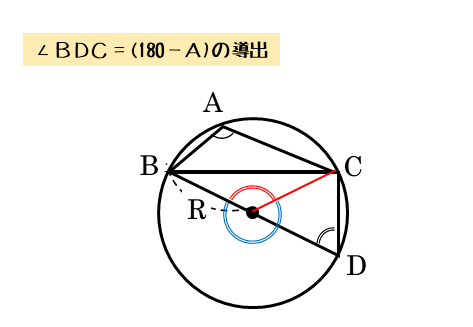
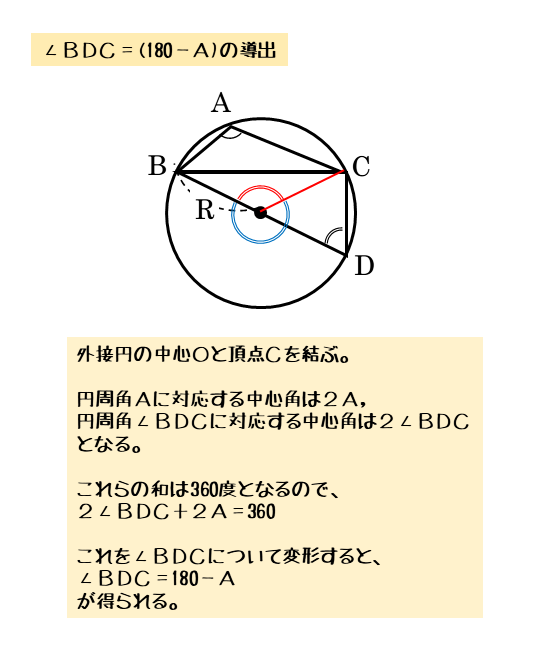
∠D=180-∠Aの証明
中心角と円周角の性質を利用して導出します。
図を見ると、∠Aと∠Dは四角形ABDCの対角になっています。ですから、∠A+∠D=180°は円に内接する四角形について成り立つ関係と言えます。
中心角と円周角の性質を利用する
\begin{align*} \quad 2\angle A + 2\angle D &= 360^{\circ} \\[ 7pt ] \angle A + \angle D &= 180^{\circ} \\[ 7pt ] \therefore \ \angle D &= 180^{\circ} – \angle A \end{align*}円に内接する四角形の対角の和は180°
次は、直角三角形の場合です。
直角三角形とその外接円の場合
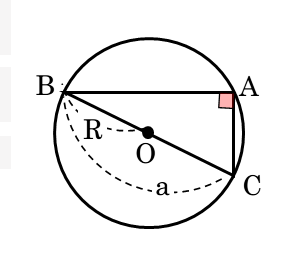
直角三角形である△ABCとその外接円Oを考えます。辺の長さや角の大きさなどの条件は少し変わります。
図形の定義
$\triangle ABC$ と外接円 $O$ について、$\angle A =90^{\circ}$、円 $O$ の半径を $R$ とすると
\begin{align*} \quad BC = a = 2R \end{align*}また、$\angle A$ に対する正弦を $\sin A$ とおく。
三角比は鋭角に対して定義されていて、直角に対して定義されていません。ですから、少し違った形で導出します。まず、辺BCと外接円の半径の関係を利用します。
辺BCと外接円の半径の関係を利用する
\begin{align*} \quad 2R = a \end{align*}両辺を $\sin A$ で割ると
\begin{align*} \quad \frac{2R}{\sin A} = \frac{a}{\sin A} \end{align*}ここから左辺だけを変形していきます。ここで、三角比の拡張を利用します。
三角比の拡張を利用する
$\angle A = 90^{\circ}$ より
\begin{align*} \quad \frac{2R}{\sin 90^{\circ}} = \frac{a}{\sin A} \end{align*}ここで、$\sin 90^{\circ} = 1$ より
\begin{align*} \quad 2R = \frac{a}{\sin A} \end{align*}直角三角形のときでも同じ式を導出することができました。この式は∠B,∠Cについても成り立ちます。
このように、どんな三角形であっても外接円との関係は同じ等式で表すことができます。これが正弦定理です。