中学数学｜正負の数の加減算について
前回の記事で、正負の数が持つ意味について触れました。正負の数は算数のときに扱っていた数と異なるので注意が必要です。
今回は、正負の数の加減算について学習します。整式の加減算にも関わってくるので、きちんとマスターしておきましょう。
正負の数の加減算
「数式を日本語に翻訳できるようになることが、数学ができるようになる近道だ」という話を聞いたことがあり、なるほどと思った記憶あります。
問題の文言から立式するのが良い例だと思います。英文を訳すように、式も言葉と対応させて学習するようにすれば、もっと解ける問題が増えるのではないでしょうか。
そのきっかけを正負の数の加減算で練習してみましょう。
正負の数の加算
正負の数の加減算を解説する方法には色々ありますが、共通しているのが、数式を言葉で理解させようとしている点です。
たとえば、次の加算を考えます。
例題
次の計算をせよ。
\begin{align*} &\quad 1. \quad \left(+1 \right)+\left(+3 \right) \\[ 7pt ] &\quad 2. \quad \left(+1 \right)+\left(-3 \right) \\[ 7pt ] &\quad 3. \quad \left(-3 \right)+\left(+1 \right) \\[ 7pt ] &\quad 4. \quad \left(-1 \right)+\left(-3 \right) \end{align*}それぞれの式を言葉で考えるとき、加算（加法）の計算記号（＋）は「足す」「加える」「進む」などの言葉に置き換えます。それぞれの加算の式を、数直線も利用して言葉に置き換えてみます。
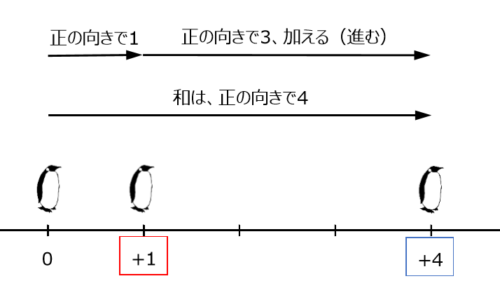
１番目の式について、数直線上の点（ペンギン）の動きで考えてみると、以下のように説明できます。
- 正の向きに絶対値が１である＋１に対応する点に対して、
- 正の向きを向いて、絶対値が３のぶんだけ進める（＝加える）と、
- その結果、＋１に対応する点は＋４に対応する点に移動した。
例題１の計算結果
\begin{align*} \quad &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+4 \end{align*}正負の数は向きと原点からの距離（＝絶対値）をもつ数です。符号を見て向き、数字を見て絶対値というように分けて考えます。
算数のときのように数の大きさを求めるだけの計算ではなく、基準に対する点の位置を求めようとする計算になっています。
また、加算では、符号で指定された向きに点をそのまま進める（加える）計算になっています。
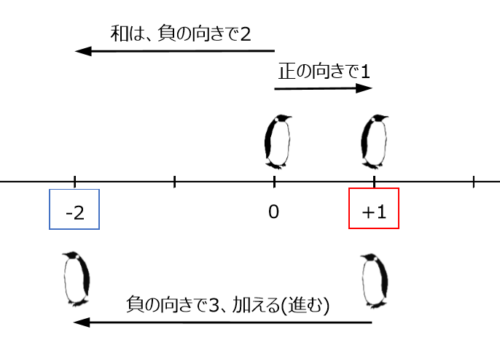
２番目の式も同様に考えます。
- 正の向きに絶対値が１である＋１に対応する点に対して、
- 負の向きを向いて、絶対値が３のぶんだけ進める（＝加える）と、
- その結果、＋１に対応する点は－２に対応する点に移動した。
言葉に置き換えると分かるように、減算していないことが分かります。
例題２の計算結果
\begin{align*} \quad &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-2 \end{align*}マイナス（－）は符号であって、減算の計算記号ではない。
３番目と４番目の加算も同様に考えていくと、加算の結果は以下のようになります。
例題３の計算結果
\begin{align*} \quad &\left(-3 \right)+\left(+1 \right) \\[ 7pt ] = \ &-2 \end{align*}例題４の計算結果
\begin{align*} \quad &\left(-1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-4 \end{align*}加算から分かるルール
例題のような加算の結果から、何らかの規則性がないかを考えてみます。
加算の式とその結果から、正負の数の組合せが規則性を与えていることに気付きます。
加算の式とその結果
\begin{align*} \quad 1. \quad &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+4 \\[ 10pt ] 2. \quad &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-2 \\[ 10pt ] 3. \quad &\left(-3 \right)+\left(+1 \right) \\[ 7pt ] = \ &-2 \\[ 10pt ] 4. \quad &\left(-1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-4 \end{align*}１，４番目のように、２数が同符号のとき、加算後の符号と数字（＝絶対値）について以下のようなことが分かります。
同符号の２数の加算
- 加算後の符号は、２数と同じ。
- 加算後の絶対値は、２数の絶対値の和になる。
また、２，３番目のように、２数が異符号のとき、以下のようになります。
異符号の２数の加算
- 加算後の符号は、絶対値が大きい方の数と同じ。
- 加算後の絶対値は、２数の絶対値の差になる。
この規則性を利用すれば、正負の数の組合せから加算後の数を求めることができます。
正負の数の符号と絶対値を分けて扱う。
規則性に合わせた計算過程は以下のようになります。
符号の組合せと絶対値の大小で計算する
\begin{align*} \quad 1. \quad &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+\left(1+3 \right) \\[ 7pt ] = \ &+4 \\[ 10pt ] 2. \quad &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-\left(3-1 \right) \\[ 7pt ] = \ &-2 \\[ 10pt ] 3. \quad &\left(-3 \right)+\left(+1 \right) \\[ 7pt ] = \ &-\left(3-1 \right) \\[ 7pt ] = \ &-2 \\[ 10pt ] 4. \quad &\left(-1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-\left(1+3 \right) \\[ 7pt ] = \ &-4 \end{align*}規則性を利用した計算は、正負の数の乗除算でも出てくるので、早く慣れておきたいところです。
交換法則と結合法則
２，３番目の式から分かるように、加算では数が入れ替わっても結果が等しくなります。このことを交換法則といいます。
加算では交換法則が成り立つ
\begin{align*} \quad 2. \quad &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-2 \\[ 10pt ] 3. \quad &\left(-3 \right)+\left(+1 \right) \\[ 7pt ] = \ &-2 \end{align*}また、正負の数の加算では、計算の優先順位を変えて計算できる結合法則も成り立ちます。
結合法則の例
\begin{align*} ex1. \\[ 5pt ] \quad &\left(1+3 \right)+5 \\[ 7pt ] = \ &4+5 \\[ 7pt ] = \ &9 \\[ 10pt ] ex2. \\[ 5pt ] \quad &1+\left(3+5 \right) \\[ 7pt ] = \ &1+8 \\[ 7pt ] = \ &9 \end{align*}正負の数の加算では、交換法則と結合法則が成り立ちます。ですから、左から順に計算しなくても良いのです。
正負の数の加算では、交換法則や結合法則が成り立つ。
数が３つ以上になると、交換法則や結合法則は非常に役立ちます。