図形と方程式|円の方程式の決定について

円の方程式の決定を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
次の円の方程式を求めよ。
$(1)$ $2$ 点 $(0 \ , \ 2) \ , \ (-1 \ , \ 1)$ を通り、中心が直線 $y=2x-8$ 上にある。
$(2)$ 点 $(2 \ , \ 3)$ を通り、$y$ 軸に接して中心が直線 $y=x+2$ 上にある。
$(3)$ 点 $(4 \ , \ 2)$ を通り、$x$ 軸、$y$ 軸に接する。
問(1)の解答・解説
問(1)
次の円の方程式を求めよ。
$2$ 点 $(0 \ , \ 2) \ , \ (-1 \ , \ 1)$ を通り、中心が直線 $y=2x-8$ 上にある。
円の方程式を決定する問題では、基本的に中心と半径を求める問題です。例題のように、中心の座標を設定することから始めましょう。
例題と同じ要領で作図します。中心の座標なども追記しておくと良いでしょう。図は以下の通りです。
問(1)では、円が軸に接するわけではないので、半径が不明のままです。ただ、円周上の2点の座標が分かっているので、これを上手く利用します。
円の定義より、中心と円周上の点との距離(=半径)はつねに一定であることを利用します。
問(1)の解答例 1⃣
円が直線 $y=2x-8$ 上にあるので、中心の座標は
\begin{align*} \quad (a \ , \ 2a-8 ) \end{align*}と表される。
中心と円周上の点との距離は一定なので
\begin{align*} \quad \sqrt{(a-0)^{2}+(2a-8-2)^{2}}=\sqrt{(a+1)^{2}+(2a-8-1)^{2}} \end{align*}両辺を2乗して整理すると
\begin{align*} &\quad (a-0)^{2}+(2a-8-2)^{2}=(a+1)^{2}+(2a-8-1)^{2} \\[ 7pt ] &\quad a^{2}+(2a-10)^{2}=(a+1)^{2}+(2a-9)^{2} \\[ 7pt ] &\quad a^{2}+4a^{2}-40a+100=a^{2}+2a+1+4a^{2}-36a+81 \\[ 7pt ] &\quad -6a=-18 \\[ 7pt ] &\quad \therefore \ a=3 \end{align*}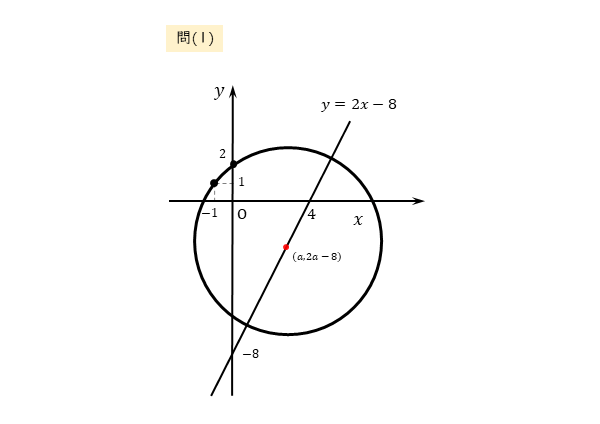
中心のx座標が分かったので、y座標と半径をそれぞれ求めます。中心と半径が分かったら、基本形に代入しましょう。
問(1)の解答例 2⃣
\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \therefore \ a=3 \end{align*}よって、中心の座標は
\begin{align*} \quad (3 \ , \ -2 ) \end{align*}となるので、半径は
\begin{align*} \quad \sqrt{(3-0)^{2}+(-2-2)^{2}}=5 \end{align*}よって、求める円の方程式は
\begin{align*} \quad (x-3)^{2}+(y+2)^{2}=25 \end{align*}なお、円周上の2点では一般形を利用しても解けません。一般形を利用するときは、円周上の点が少なくとも3点与えられている必要があります。
問(1)の別解例
これまでの知識を利用すれば、別解例のような解法もあります。
円周上の2点を通る直線に垂直な直線を考えます。
この直線が円周上の2点を結んだ線分の中点を通るとき、求める円の中心も通るはずです。このことを利用します。
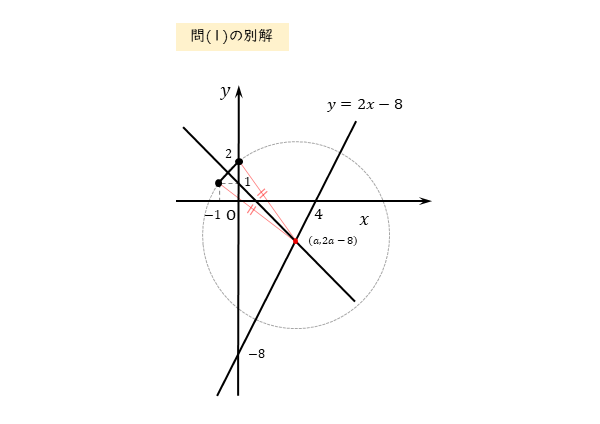
別解例は以下の通りです。
問(1)の別解例
円は $2$ 点 $A(0 \ , \ 2) \ , \ B(-1 \ , \ 1)$ を通る。
これより、円の中心は2点から等距離の位置にある。すなわち、円の中心は線分 $AB$ の垂直二等分線上にある。
線分 $AB$ の中点の座標は
\begin{align*} \quad \left( \frac{0+(-1)}{2} \ , \ \frac{2+1}{2} \right) \end{align*}より
\begin{align*} \quad \left( -\frac{1}{2} \ , \ \frac{3}{2} \right) \end{align*}また、直線 $AB$ の傾きは
\begin{align*} \quad \frac{1-2}{-1-0}=1 \end{align*}よって、直線 $AB$ の垂直二等分線の方程式は
\begin{align*} \quad y-\frac{3}{2}=-\left( x+\frac{1}{2} \right) \end{align*}より
\begin{align*} \quad y=-x+1 \end{align*}これと直線 $y=2x-8$ の交点が円の中心となる。
$2$ 直線の方程式を連立させて解くと
\begin{align*} \quad x=3 \ , \ y=-2 \end{align*}より、中心の座標は
\begin{align*} \quad ( 3 \ , \ -2 ) \end{align*}また、半径を $r$ とすると
\begin{align*} \quad r^{2}=(3-0)^{2}+(-2-2)^{2}=25 \end{align*}したがって、求める円の方程式は
\begin{align*} \quad (x-3)^{2}+(y+2)^{2}=25 \end{align*}問(2)の解答・解説
問(2)
次の円の方程式を求めよ。
点 $(2 \ , \ 3)$ を通り、$y$ 軸に接して中心が直線 $y=x+2$ 上にある。
円が軸に接するので注意しましょう。答案を作成する前に、作図を済ませておきましょう。
図から分かるように、円がy軸に接するので、中心のx座標を半径に利用できます。
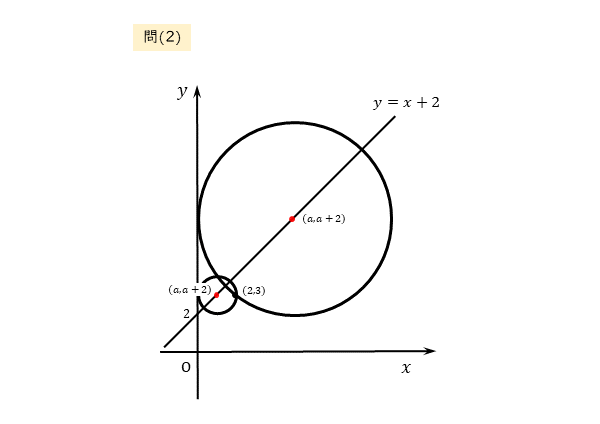
問(2)でも、円の中心を設定することから始めましょう。
問(2)の解答例
中心が直線 $y=x+2$ 上にあるので、その座標は
\begin{align*} \quad ( a \ , \ a+2 ) \end{align*}と表される。
また、円が $y$ 軸に接するので、中心と $y$ 軸の距離 $|a|$ は半径に等しい。
よって、円の方程式は
\begin{align*} \quad (x-a)^{2}+\left\{y-(a+2) \right\}^{2}=a^{2} \end{align*}これが点 $( 2 \ , \ 3 )$ を通るので
\begin{align*} \quad (2-a)^{2}+\left\{3-(a+2) \right\}^{2}=a^{2} \end{align*}これを解くと
\begin{align*} &\quad 4-4a+a^{2}+1-2a+a^{2}=a^{2} \\[ 7pt ] &\quad a^{2}-6a+5=0 \\[ 7pt ] &\quad (a-1)(a-5)=0 \\[ 7pt ] &\quad \therefore \ a=1 \ , \ 5 \end{align*}よって、求める円の方程式
\begin{align*} &\quad (x-1)^{2}+(y-3)^{2}=1 \\[ 7pt ] &\quad (x-5)^{2}+(y-7)^{2}=25 \end{align*}解答例や2次関数の決定のように、円の方程式を先に立式しておき、後で代入する形の方が分かりやすいでしょう。
もちろん、中心と円周上の点との距離が半径に等しいことから方程式を導いても構いません。ただし、この場合でも中心の座標を設定する必要があります。
円の方程式を求める問題では、複数あることが多いので注意しましょう。
問(3)の解答・解説
問(3)
次の円の方程式を求めよ。
点 $(4 \ , \ 2)$ を通り、$x$ 軸、$y$ 軸に接する。
円がx軸とy軸の両方に接します。例題と同じ要領で解けそうです。答案を作成する前に、作図を済ませておきましょう。
例題と問(3)の違いは、中心に関する情報がないことです。
ただし、問(3)では、円が通る1点が与えられています。この点から円が第1象限にあることが分かります。
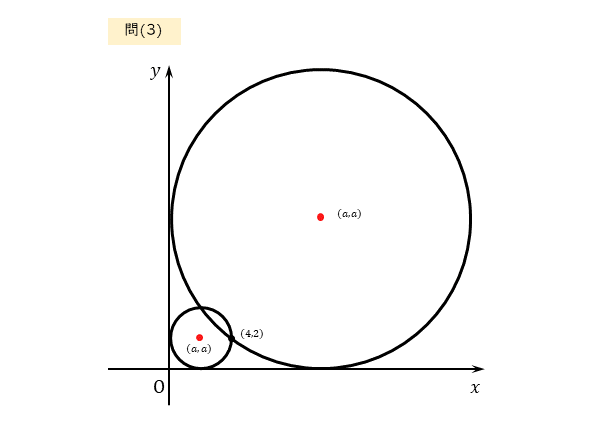
また、円がx軸とy軸の両方に接することから、中心の座標を設定することは難しくありません。円の方程式を表すことができたら、与えられた点の座標を利用しましょう。
問(3)の解答例
求める円は $x$ 軸、$y$ 軸に接し、第1象限の点 $(4 \ , \ 2)$ を通る。
よって、中心の座標は
\begin{align*} \quad ( a \ , \ a ) \end{align*}また、半径は
\begin{align*} \quad a \quad (a \gt 0) \end{align*}よって、円の方程式は
\begin{align*} \quad (x-a)^{2}+(y-a)^{2}=a^{2} \end{align*}これが点 $( 4 \ , \ 2 )$ を通るので
\begin{align*} \quad (4-a)^{2}+(2-a)^{2}=a^{2} \end{align*}これを解くと
\begin{align*} &\quad 16-8a+a^{2}+4-4a+a^{2}=a^{2} \\[ 7pt ] &\quad a^{2}-12a+20=0 \\[ 7pt ] &\quad (a-2)(a-10)=0 \\[ 7pt ] &\quad \therefore \ a=2 \ , \ 10 \end{align*}これらは、$a \gt 0$ を満たす。
よって、求める円の方程式は
\begin{align*} &\quad (x-2)^{2}+(y-2)^{2}=4 \\[ 7pt ] &\quad (x-10)^{2}+(y-10)^{2}=100 \end{align*}単に「円がx軸とy軸に接する」という条件だけでは、どの象限でも問題ありません。中心を通る直線が指定されたり、円が通る点が指定されたりして、円の位置が決まります。
条件をしっかり読み取り、作図でイメージを膨らませましょう。
Recommended books
さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。
難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。
傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。
◆特長◆大学入試の基本となる問題を扱った問題集です。問題数は138問です。問題集は問題、解答という流れが一般的ですが、本問題集はその問題のアプローチの仕方、解答から得られる色々な意味なども「ブラッシュアップ」「ちょっと一言」などを通して解説しています。問題編冊子44頁、解答編冊子224頁の構成となっています。◆自分にあったレベルが選べる!◆
- 基礎レベル
- 共通テストレベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
- 私大標準・国公立大レベル
- 私大上位・国公立大上位レベル
ここで紹介する問題集は、『大学入試 全レベル問題集 数学』シリーズです。昔からある有名なレベル別問題集です。
3年の1学期までに基礎レベル1を解いて、教科書内容の補完をしてしまいましょう。夏休みになったら、共通テストレベル2で実戦練習をこなすと良いでしょう。9月~10月くらいまでにこの2冊を何度も周回して仕上げれば、秋からの2次対策にスムーズに移行できるでしょう。
なお、新入試に対応するための改訂版が2020年2月に出版されています。改訂版を希望する場合、「新入試対応」とあるものを購入しましょう。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 円の方程式の決定では、基本形を利用しよう。
- 中心と円周上の点との距離は半径に等しい。
- 軸に接する円の半径は、中心の座標を利用しよう。
- 中心の座標を半径にそのまま使わないようにしよう。
- 絶対の扱い方に慣れておこう。













