図形の性質|作図について

角の二等分線を引こう
角の二等分線とは、角の大きさを二等分する直線のことです。
∠AOBの二等分線を引いてみましょう。手順は3つあります。
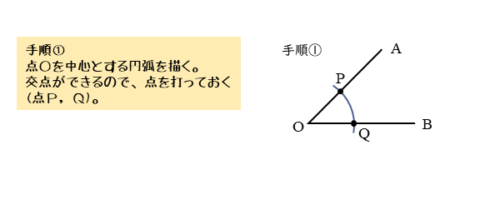
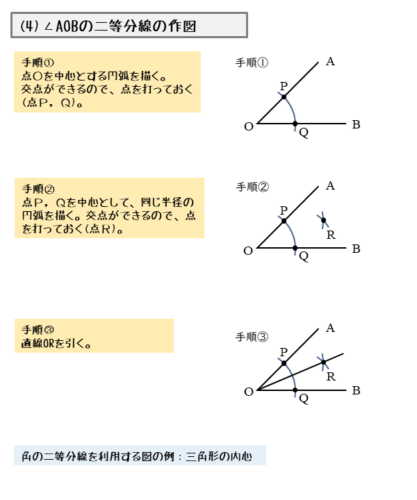
角の二等分線の手順①
コンパスを使って、点Oを中心とする円(弧)を描きます。コンパスを開いたままにしておきます。
角をつくる線分OA,OB上にそれぞれ交点ができます。それぞれの交点をP,Qとすると、OP=OQです。
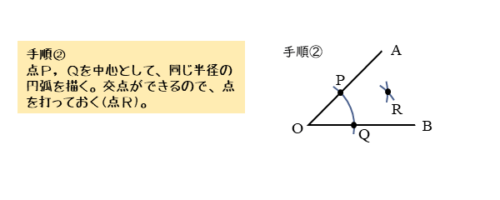
角の二等分線の手順②
手順①と同じ要領でコンパスを使って、今度は点P,Qをそれぞれ中心とする円(弧)を描きます。
2つの円(弧)が交わって交点ができます。この交点をRとすると、同じ半径の円(弧)を描いたのでOP=OQ=PR=QRです。これまでと同じように、4辺が等しい四角形(ひし形)ができます。
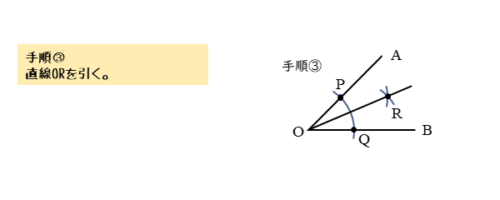
角の二等分線の手順③
2点O,Rを通る半直線ORを定規で引きます。この半直線ORが∠AOBの二等分線です。
角の二等分線かどうかを調べてみよう
半直線ORが∠AOBの二等分線であることを確かめてみましょう。
作図の様子から分かるように、線分OR,PQは、ひし形OPRQの対角線です。ですから、これらは直交し、互いに他を二等分します。このことと△OPQが二等辺三角形であることに注目します。
二等辺三角形である△OPQにおいて、線分ORは、底辺PQの垂直二等分線となるだけでなく、頂角の二等分線にもなります。
ですから、頂角である∠POQは、線分ORによって二等分されます。したがって、半直線ORは∠AOBの二等分線になります。
二等辺三角形において、底辺の垂直二等分線は、頂角の二等分線でもある。
角の二等分線の性質
垂直二等分線と同じように、角の二等分線がもつ性質も頻出なので覚えておきましょう。
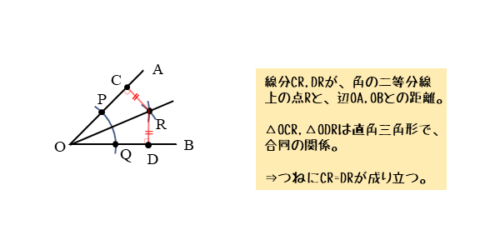
角の二等分線がもつ性質として、∠AOBの二等分線上の点から、2辺OA,OBまでの距離が等しい(CR=DR)という性質があります。
点Rが∠AOBの二等分線上のどこにあっても、△OCRと△ODRは合同な直角三角形になるからです。ここで、点と線分との距離は、2点間の距離とは異なり、点から線分に引いた垂線の長さになるので注意しましょう。
このことから、∠AOBの二等分線は、交わる2つの定直線OA,OBから等距離にある点の集まり(軌跡)になります。このような角の二等分線は、たとえば内心を作図するときに利用されます。
角の二等分線は、内心を作図する問題で出題される。
角の二等分線を引く手順の一覧です。
点を通る平行線を引こう
平行線とは、すでに引かれた直線や線分に対して平行な直線のことです。
直線ℓに対して、点Aを通る平行線を引いてみましょう。ただし、点Aは直線ℓ上にない点です。手順は3つあります。
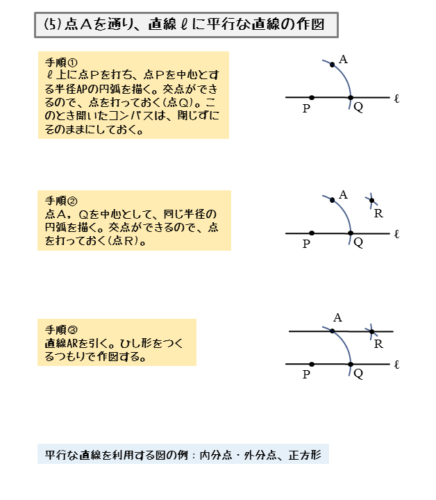
平行線の手順①
直線ℓ上に、点Pをつくります。コンパスを使って、点Pを中心とする半径APの円(弧)を描きます。コンパスを開いたままにしておきます。
円(弧)と直線ℓの交点ができるので、この交点をQとします。このときAP=PQです。
平行線の手順②
手順①と同じ要領でコンパスを使って、今度は点A,Qをそれぞれ中心とする円(弧)を描きます。
2つの円(弧)が交わって交点ができます。ただし、交点は点Pと反対側に作りましょう。
交点をRとすると、同じ半径の円(弧)を描いたのでAP=PQ=AR=QRです。これで4辺が等しい四角形(ひし形)ができます。
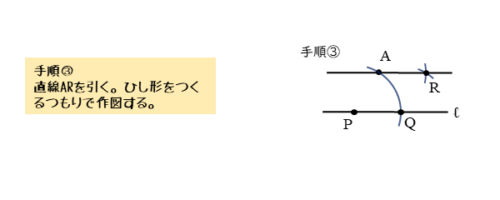
平行線の手順③
2点A,Rを通る直線を定規で引きます。この直線ARが、点Aを通る平行線です。
直線ARが、直線ℓの平行線であることを確かめてみましょう。
作図するときにコンパスの開きを変えていないので、四角形APQRはひし形です。ひし形は平行四辺形の性質をもつので、2組の対辺は平行で、長さが等しくなっています。ですから、直線ARは、直線ℓに対して平行な直線になります。
特定の点を通る平行線を引く手順の一覧です。
角を移して平行線を作図する
角の移し方
なお、平行線の作図は、ひし形をつくる代わりに、垂線を繰り返し作図することでも可能です。
その他には、基本作図の「角を移す」方法もあります。「角を移す」方法は、繰り返し垂線を作図するよりも主流になっています。
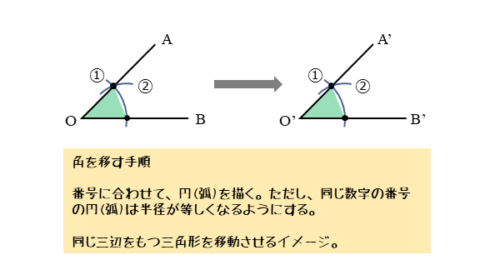
角を移す作図では、移動側に合同な三角形をつくるイメージをもつと分かりやすいです。
注意したいのは、移す角の大きさは60°とは限らないので、コンパスの開き方を変える必要があるということです。同じ開き方だと正三角形ができてしまいます。
∠AOBと同じ大きさの∠A’O’B’を作るとします。右図の初期状態は、線分O’B’だけがある状態です。
図の番号に従って円(弧)を描いていきます。ここで、同じ番号の円(弧)は同じ半径になるようにします。
初めに点Oを中心として円(弧)を描きます。すると、線分OA,OB上に交点ができます(①)。コンパスの開きはそのままで、これと同じことを線分O’B’にも行います。
次に交点間の長さを測ります(②)。おそらく①のときの半径とは異なるので、コンパスの開きが変わっても構いません。
長さを測ったコンパスの開きのままで、これと同じことを線分O’B’にも行います。移す方に交点ができるので、定規で直線を引くと同じ大きさの角をつくることができます。
角を移す方法で平行線を引く
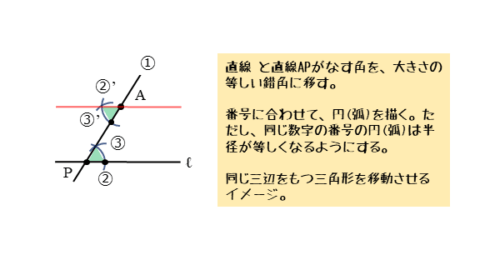
平行線を引くとき、角を移す方法を利用すると、∠APQと大きさの等しい角を錯角となるように移すことで作図できます。
コンパスの開き具合を∠APQに合わせて変えることに注意が必要ですが、ひし形を作図する方法と併せて覚えておきましょう。
次は、実際に作図を扱った問題を解いてみましょう。