集合と論理｜逆、裏、対偶について

11/27/2021数学１

逆、裏、対偶を扱った問題を解いてみよう

次の問題を考えてみましょう。

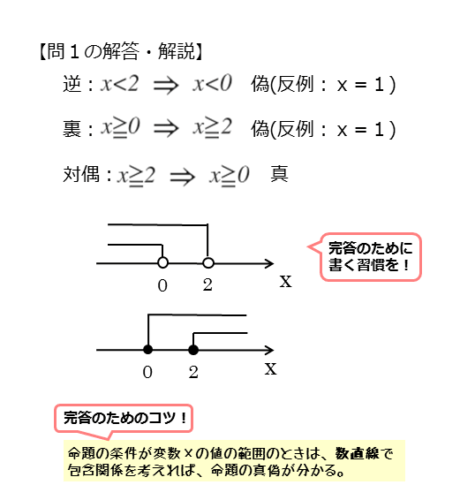
問１の解答・解説

問１

次の命題の逆、裏、対偶をつくり、それらの真偽を調べよ。

\begin{align*} \quad x \lt 0 \ \Rightarrow \ x \lt 2 \end{align*}

問１は、与えられた命題の逆、裏、対偶とその真偽を求める問題です。

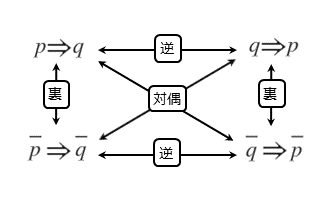
命題の逆は、仮定と結論を入れ替えたものです。命題の裏は、仮定と結論をそれぞれ否定したものです。

命題の対偶は、逆の裏を求めるか、裏の逆を求めるかのどちらかで得られます。

図からも分かるように、対偶は必ず逆と裏を経てつくられます。

命題の逆、裏、対偶をつくると以下のようになります。

問１の解答例 1⃣

命題「 $x \lt 0 \ \Rightarrow \ x \lt 2$ 」の逆、裏、対偶を求めると

命題の逆「 $x \lt 2 \ \Rightarrow \ x \lt 0$ 」

命題の裏「 $x \geqq 0 \ \Rightarrow \ x \geqq 2$ 」

命題の対偶「 $x \geqq 2 \ \Rightarrow \ x \geqq 0$ 」

命題の逆、裏、対偶が分かったら、それぞれの真偽を調べます。仮定や結論が不等式で与えられています。このような場合、数直線を利用すると、真偽を簡単に調べることができます。

問１の解答例 2⃣

命題の逆「 $x \lt 2 \ \Rightarrow \ x \lt 0$ 」の真偽を調べると

$x \lt 2$ を満たす実数は、$x \lt 0$ を満たすとは限らない。

反例は $x=1$ のとき。

よって、命題の逆は偽である。

命題の裏「 $x \geqq 0 \ \Rightarrow \ x \geqq 2$ 」の真偽を調べると

$x \geqq 0$ を満たす実数は、$x \geqq 2$ を満たすとは限らない。

反例は $x=1$ のとき。

よって、命題の裏は偽である。

命題の対偶「 $x \geqq 2 \ \Rightarrow \ x \geqq 0$ 」の真偽を調べると

$x \geqq 2$ を満たす実数は、すべて $x \geqq 0$ を満たす。

よって、命題の対偶は真である。

問１のポイントと解答例をまとめると以下のようになります。

命題の逆、裏、対偶は、十分条件や必要条件を扱った問題とも関係しています。

一般に、出題される問題では、命題の真偽がはっきりしません。ですから、まず命題の真偽を調べる必要があります。このとき、対偶を利用することがあります。そして、その真偽をもとに十分条件か必要条件かを吟味します。

問２の解答・解説

問２

次の命題を証明せよ。

整数 $n$ について、$n^{2}$ が偶数ならば、$n$ は偶数である。

問２は、与えられた命題を証明する問題です。もう少しことばを補うと、「与えられた命題が真である（＝正しい）ことを証明しなさい」という問題です。本質的には、命題の真偽を調べる問題と変わりません。

証明問題では、与えられた事柄が成り立つことは当たり前なので、この問題の命題が真であることは決まっています。

しかし、この命題の真偽を調べるのは少し面倒です。

仮定を見ると「ｎ²が偶数」とあります。基本通りにｎ²＝２ｋとおいてしまうと、変数ｎの値が無理数になります。ｎ²を上手に表せないと上手くいきそうにありません。

このようなとき、命題の対偶を利用します。与えられた命題の対偶を求めます。

問２の解答例 1⃣

命題「整数 $n$ について、$n^{2}$ が偶数ならば、$n$ は偶数である。」の対偶は

「整数 $n$ について、$n$ が奇数ならば、$n^{2}$ は奇数である。」

となる。

命題の対偶をつくると、仮定が「変数ｎが奇数」となります。これなら無理数が出てきません。

変数ｎを奇数であることが分かる式で表し、ｎ²に代入します。実際に計算し、結論が成り立つかを調べます。

問２の解答例 2⃣

対偶の真偽を調べる。

$n$ が奇数であるとき

\begin{align*} \quad n=2k+1 \end{align*}

とおく。ただし、$k$ は整数。

このとき

\begin{align*} \quad n^{2} &=\left(2k+1 \right)^{2} \\[ 7pt ] &=4k^{2}+4k+1 \\[ 7pt ] &=2\left(2k^{2}+2k \right)+1 \end{align*}

より、$n^{2}$ は奇数である。

よって、命題の対偶は成り立つ。

対偶が証明されたので、もとの命題も成り立つ。

命題とその対偶の真偽は一致することを利用して、もとの命題の真偽を間接的に判定します。

問２のポイントと解答例をまとめると以下のようになります。

証明問題では、具体的な数を使わず、式で一般化して証明します。整数問題もセンター試験に出題されるようになりましたが、高校の授業では対策が充分ではないので、自分でしっかり準備しておくことが必要です。

偶数は２の倍数、奇数は（偶数±１）。ｋを整数とすると、偶数は２ｋ、奇数は２ｋ±１と表せる。

Recommended books

お勧めする２冊で紹介されている勉強法は、あくまでも彼・彼女が作り上げた勉強法なので、それらがそのまま使えるわけではないかもしれません。

しかし、成績がなかなか上がらなかったり、資格や検定の試験で不合格になったりすると、自分の勉強法に自信が持てなくなることがあります。そんなときに一読すると、自分の勉強法に足りない部分が見えてくるかもしれません。

人それぞれに勉強法はあると思いますが、根本的な部分にそう変わりはありません。変わるとすればアプローチの仕方ではないでしょうか。性格や環境などが異なるので、自分に合ったアプローチの仕方を考えなくてはなりません。

お勧めの２冊は、自分なりの勉強法を確立する上で、その助けになるかと思います。

オススメその１

東大生クイズ王で有名な伊沢拓司さん渾身の書き下ろしです。彼自身の「勉強法」を知ることができるのが本書です。

高校時代、クイズ界で「知識のモンスター」として名を成しましたが、その一方で学業がおろそかになってしまいました。そのため、成績は学年で下から数えるほどに……。

そこから彼なりに勉強法を分析し、実践して、みごと東大合格を勝ち取りました。本書では、勉強法だけでなく、クイズ王の暗記術やノート術なども公開されています。

東大生クイズ王・伊沢拓司、渾身のＡＬＬ書き下ろし！

東大生クイズ王・伊沢拓司が、自身の「勉強法」を一から解き明かします。その他、クイズ王の暗記術、ノート術など、伊沢氏が考える「勉強の骨肉」を一挙大公開!

第１章なぜ受験勉強をするのか？

第２章勉強法こそが大事だ

第３章「受験生活」への入り方

第４章成績の読み方が視界をクリアにする

第５章「たかが暗記」とまだ言うか?

第６章曇りなき思考で見定め、決める

第７章教科ごとの特徴をつかめ

第８章合格の先、不合格の先

勉強大全ひとりひとりにフィットする1からの勉強法

created by Rinker

オススメその２

東大文１に現役で合格し、司法試験予備試験を在学中に合格した、鈴木光さん。大学卒業後は、弁護士の夢を叶えることに集中されるそうです。

本書では、彼女の実践している、「勉強の計画」「問題の解法」「暗記法」「勉強の継続方法」などが系統立てて説明されています。良書です。

定期テスト、入試、資格試験…すべてに使える勉強の“基本”が網羅されているので、吸収できれば応用が利くでしょう。夢や目標を叶えるための効率的な学びのメソッドを学べます。

「みなさんの家庭教師になったつもりでこの本を書きました」

ＴＶ出演多数の東大生・鈴木光による初の著書！

はじめに

序章探る勉強目標・計画を立ててみよう

第１章知る問題を解くための「考え方」を身につけて勉強を始めよう

第２章憶える知識を自分のものにしよう

第３章整える勉強を続けられる環境をつくろう

第４章正す結果を振り返ってやり方を修正してみよう

第５章突破する科目別の攻略法

終章さまざまな学ぶ場

おわりに

特別コラム

夢を叶えるための勉強法

created by Rinker

オススメその３

数学だけに限らず、高校での学習をスムーズに進めていくには「読解力」や「論理的な思考力（地頭がいい）」などが必要ではないかと思います。数学Ａでは特に必要だと思います。

これらはどちらかと言うと、短期間で身に付くものではなく、長期間の経験によって習得できるものです。ただ、大事なことなのに習得に時間が掛かるのはリスクが高すぎますし、方法論も知らずに取り組んでいても習得できるかも分かりません。

そこでお勧めしたいのが『「読む力」と「地頭力」がいっきに身につく東大読書』です。

マネするだけで、誰でも、どんな本でも！

速く読める

内容を忘れない

応用できる

東大生は、そんな超・実践的な読書術を自然と習得していました。ホントは教えたくなかったノウハウを、一冊に凝縮します！

一生使える５つの「スゴい読み方」

「読み込む力」を劇的に上げる…仮説作り

「論理の流れ」がクリアに見える…取材読み

「一言で説明する力」を鍛える…整理読み

「多面的なモノの見方」を身につける…検証読み

「ずっと覚えている」ことができる…議論読み