数学2
2点間の距離と三角形の形状を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
\begin{align*}
&\text{$3$ 点 $A(1 \ , \ 1) \ , \ B(2 \ , \ 4) \ , \ C(a \ , \ 0)$ を頂点とする $\triangle {ABC}$ について} \\[ 5pt ]
&(1) \quad \text{$\triangle {ABC}$ が直角三角形となるとき、$a$ の値を求めよ。} \\[ 10pt ]
&(2) \quad \text{$\triangle {ABC}$ が二等辺三角形となるとき、$a$ の値を求めよ。}
\end{align*}
問(1)の解答・解説
問(1)
\begin{align*}
&\text{$3$ 点 $A(1 \ , \ 1) \ , \ B(2 \ , \ 4) \ , \ C(a \ , \ 0)$ を頂点とする $\triangle {ABC}$ について} \\[ 5pt ]
&\text{$\triangle {ABC}$ が直角三角形となるとき、$a$ の値を求めよ。}
\end{align*}
3つの頂点のうち、点Cのx座標が不明です。ただし、点Cのy座標が0なので、点Cはx軸上にあります。
また、△ABCが直角三角形であることが条件です。直角三角形であるための条件は、三平方の定理が成り立つことです。どの内角が直角であるかを考える必要があります。
まずは、3辺の長さを調べます。ただし、三平方の定理のことを考えて、長さを2乗しておきます。
問(1)の解答例 1⃣
\begin{align*}
&\quad A(1 \ , \ 1) \ , \ B(2 \ , \ 4) \ , \ C(a \ , \ 0) \\[ 7pt ]
&\text{$3$ 辺の長さについて} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}=\left(2-1 \right)^{\scriptsize{2}}+\left(4-1 \right)^{\scriptsize{2}} \\[ 7pt ]
&\quad BC^{\scriptsize{2}}=\left(a-2 \right)^{\scriptsize{2}}+\left(0-4 \right)^{\scriptsize{2}} \\[ 7pt ]
&\quad CA^{\scriptsize{2}}=\left(1-a \right)^{\scriptsize{2}}+\left(1-0 \right)^{\scriptsize{2}} \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2
\end{align*}
3つの内角のうち、どれが直角になるかを場合分けして方程式を導きます。まず、∠BAC(∠A)が直角であるときを考えます。
問(1)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&(i) \ \angle {BAC} \ \text{が直角のとき} \\[ 5pt ]
&\quad CA^{\scriptsize{2}}+AB^{\scriptsize{2}}=BC^{\scriptsize{2}} \\[ 7pt ]
&\text{が成り立つので} \\[ 5pt ]
&\quad \left(a^{\scriptsize{2}}-2a+2 \right)+10=a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\text{整理すると} \\[ 5pt ]
&\quad 2a=8 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=4
\end{align*}
次に、∠ABC(∠B)が直角であるときを考えます。
問(1)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(ii) \ \angle {ABC} \ \text{が直角のとき} \\[ 5pt ]
&\quad AB^{\scriptsize{2}}+BC^{\scriptsize{2}}=CA^{\scriptsize{2}} \\[ 7pt ]
&\text{が成り立つので} \\[ 5pt ]
&\quad 10+\left(a^{\scriptsize{2}}-4a+20 \right)=a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&\text{整理すると} \\[ 5pt ]
&\quad 2a=28 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=14
\end{align*}
さいごに、∠ACB(∠C)が直角であるときを考えます。
問(1)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(iii) \ \angle {ACB} \ \text{が直角のとき} \\[ 5pt ]
&\quad BC^{\scriptsize{2}}+CA^{\scriptsize{2}}=AB^{\scriptsize{2}} \\[ 7pt ]
&\text{が成り立つので} \\[ 5pt ]
&\quad \left(a^{\scriptsize{2}}-4a+20 \right)+\left(a^{\scriptsize{2}}-2a+2 \right)=10 \\[ 7pt ]
&\text{整理すると} \\[ 5pt ]
&\quad a^{\scriptsize{2}}-3a+6=0 \quad \cdots \text{①} \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad a^{\scriptsize{2}}-3a+6=\left(a-\frac{3}{2} \right)^{\scriptsize{2}}+\frac{15}{4} \ \gt 0 \\[ 7pt ]
&\text{よって、①を満たす $a$ の値は存在しない。}
\end{align*}
場合分けが終わったので、3つの結果をまとめます。
問(1)の解答例 5⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&(i) \ , \ (ii) \ , \ (iii) \ \text{より} \\[ 5pt ]
&\quad a=4 \ , \ 14
\end{align*}
前もって作図をしていれば、頂点の位置関係が分かるので、考えられる直角三角形は2通りだろうと予想できます。
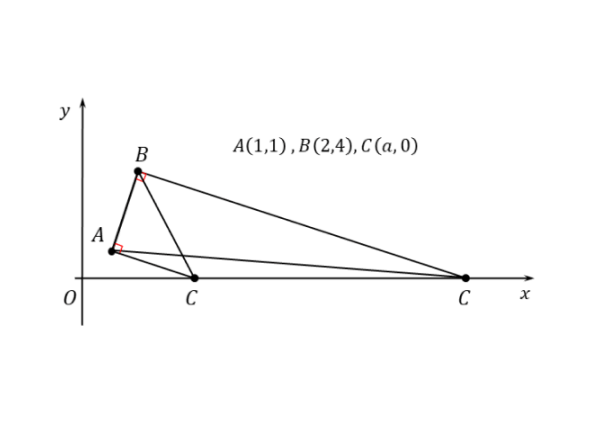 問(1)の作図
問(1)の作図
2次方程式から実数解を得られないときの扱い
解答例4⃣において、2次方程式(①式)を解いても実数解を得ることができません。
望ましいのは、①式を見て実数解が得られないことに気付くことです。いちいち解いてしまうと、二度手間になるからです。2次方程式を見て、因数分解できるかどうか、また、実数解をもつかどうかの判断が素早くできることが大切です。
2次方程式が実数解をもたないことを示すには、2次方程式の値がつねに0より大きくなることを示します。グラフで言えば、下に凸のグラフがx軸よりも上にある状態です。x軸と共有点をもたないので、2次方程式は実数解をもちません。
2次方程式の値が0より大きくなることを示すには、解答例のように平方完成します。実数の2乗が0以上になる性質と、定数項が正の数であることから、2次方程式の値はつねに正となります。判別式の値を求めても良いですが、こちらの方が一般的です。
因数分解できず、定数項が正の数であれば、2次方程式が実数解をもたない可能性を考えよう。暗算で判別式の値を考えても良い。
問(2)の解答・解説
問(2)
\begin{align*}
&\text{$3$ 点 $A(1 \ , \ 1) \ , \ B(2 \ , \ 4) \ , \ C(a \ , \ 0)$ を頂点とする $\triangle {ABC}$ について} \\[ 5pt ]
&\text{$\triangle {ABC}$ が二等辺三角形となるとき、$a$ の値を求めよ。}
\end{align*}
問(1)と異なるのは、△ABCが二等辺三角形になるということです。それ以外は同じ条件です。
3辺のうち2辺の長さが等しくなるので、その組合せを考えると3通りあります。3通りの場合分けで解きます。
3辺の長さは問(1)の結果を利用します。まず、2辺AB,BCの長さが等しいときを考えます。
問(2)の解答例 1⃣
\begin{align*}
&(1) \ \text{より} \\[ 5pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&(i) \ AB=BC \ \text{のとき} \\[ 5pt ]
&\text{$AB^{\scriptsize{2}}=BC^{\scriptsize{2}}$ より} \\[ 5pt ]
&\quad 10=a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a^{\scriptsize{2}}-4a+10=0 \quad \cdots \text{②} \\[ 7pt ]
&\text{ここで} \\[ 5pt ]
&\quad a^{\scriptsize{2}}-4a+10=\left(a-2 \right)^{\scriptsize{2}}+6 \ \gt 0 \\[ 7pt ]
&\text{よって、②を満たす $a$ の値は存在しない。}
\end{align*}
次に、2辺BC,CAの長さが等しいときを考えます。
問(2)の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(ii) \ BC=CA \ \text{のとき} \\[ 5pt ]
&\text{$BC^{\scriptsize{2}}=CA^{\scriptsize{2}}$ より} \\[ 5pt ]
&\quad a^{\scriptsize{2}}-4a+20=a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&\text{整理すると} \\[ 5pt ]
&\quad 2a=18 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=9
\end{align*}
さいごに、2辺CA,ABの長さが等しいときを考えます。
問(2)の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad AB^{\scriptsize{2}} = 10 \\[ 7pt ]
&\quad BC^{\scriptsize{2}} = a^{\scriptsize{2}}-4a+20 \\[ 7pt ]
&\quad CA^{\scriptsize{2}} = a^{\scriptsize{2}}-2a+2 \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&(iii) \ CA=AB \ \text{のとき} \\[ 5pt ]
&\text{$CA^{\scriptsize{2}}=AB^{\scriptsize{2}}$ より} \\[ 5pt ]
&\quad a^{\scriptsize{2}}-2a+2=10 \\[ 7pt ]
&\text{整理すると} \\[ 5pt ]
&\quad \left(a+2 \right)\left(a-4 \right)=0 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad a=-2 \ , \ 4
\end{align*}
場合分けが終わったので、3つの結果をまとめます。
問(2)の解答例 4⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&(i) \ , \ (ii) \ , \ (iii) \ \text{より} \\[ 5pt ]
&\quad a=-2 \ , \ 4 \ , \ 9
\end{align*}
前もって作図をしていれば、頂点の位置関係が分かるので、考えられる二等辺三角形は3通りだろうと予想できます。
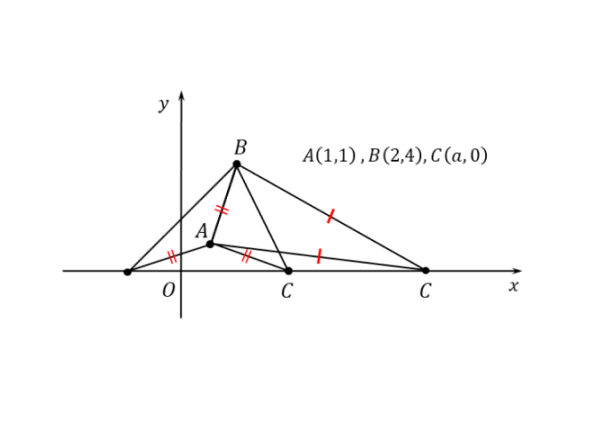 問(2)の作図
問(2)の作図
条件によっては複数の解となる場合がありますが、作図をすれば取りこぼしを回避できます。イメージを膨らませて解への道筋を立てることは、問題を解く上で重要です。
Recommended books
チャート式と言えば有名ですが、学校で配布されるのは、ほとんどが黄色か青色のどちらかです。数学を苦手にしている人にとっては、扱い辛く感じるかもしれません。ページ数も多いので尚更です。
オススメ その1
日常学習では辞書的に利用できる参考書があると助かります。有名なのは、チャート式でしょう。
チャート式は、色別にレベル分けされています。学校で配布されるのは、青や黄のチャート式が多いと思います。ただし、青や黄の内容が高度だと感じるのであれば、いっそのこと白のチャート式の方が良いかもしれません。
『チャート式基礎と演習数学1+A 増補改訂版』や『チャート式基礎と演習数学2+B 増補改訂版』では、より基礎的な内容が扱われています。教科書の内容を補完してくれるので、予習や復習を進めやすくなるでしょう。
基礎固めには白チャート。数学の苦手な生徒でも,安心して学習を進められます。教科書と併用しながらの学習や、基礎固めには最適の参考書。中堅私立大学の受験対策や、大学入学共通テストの準備にも役立つ一冊。本冊巻末に、大学入学共通テストの対策ができる「実践編」を追加。
オススメ その2
白チャートと同じように基礎的な内容を扱っているのが、スカイチャートと言われる『チャート式 絶対に身につけたい数学1+Aの基本』や『チャート式 絶対に身につけたい数学2+Bの基本』です。速習型の参考書なので、たとえば、受験勉強を何から始めれば良いのか分からない人向けの教材です。
白チャート『チャート式基礎と演習数学1+A 増補改訂版』は、560ページ(別冊解答編368ページ)あります。青チャートだと640ページ(別冊解答編404ページ)なので、白チャートも少ない方です。これらに対して、スカイチャート『チャート式 絶対に身につけたい数学1+Aの基本』は160ページ(別冊解答編88ページ)なので、かなりコンパクトにまとめられています。
使い方としては、予習や復習の際に類題をこなしたり、定期考査前の確認や仕上げに使ったりできます。また、受験勉強の準備にあたって、自分の基礎学力を短期間で確認することができます。
対象 … 教科書の内容を効率的に総復習したい人や、基礎知識を総整理したい人
特長 … 絶対に身につけたい基礎知識が詰まった良問を精選しました。「極意」では,問題を解くとき、効果的にアプローチするための手順や考え方をコンパクトにまとめました。例題と同等のレベルである練習問題を解くことで,例題の解法や基礎知識の理解度を確認できます。
参考書は紹介した教材だけではありません。大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 図形の形状を知るには、辺の長さを調べよう。
- 座標平面上の図形であれば、2点間の距離を利用して辺の長さを求めよう。
- 三角形の形状に関する問題では、直角三角形の条件に気を付けよう。
- 辺の長さは、2乗した値で求めておこう。
- 2次方程式が実数解をもつかどうかを予想できるようになろう。

















