２次関数｜関数について

04/10/2022中学数学,数学１

１次関数の式とグラフ

変数ｘ，ｙが、ｙ＝ａｘ＋ｂという式で表される関係のとき、１次関数の関係にあると言います。

文字ａ，ｂは定数です。ａのことを「傾き」、ｂのことを「切片」と言います。なお、１次関数でのａも比例定数と言うことがありますが、傾きと言う方が多いです。

また、１次関数の関係では、変数ｙは定数項をもちますが、比例と同じく変数ｘの１次式で表されます。

比例の式は、１次関数においてｂ＝０のときの式になるので、１次関数の具体例の１つと考えることができます。

１次関数の関係にあるとき、グラフの概形や特徴をまとめると以下のようになります。

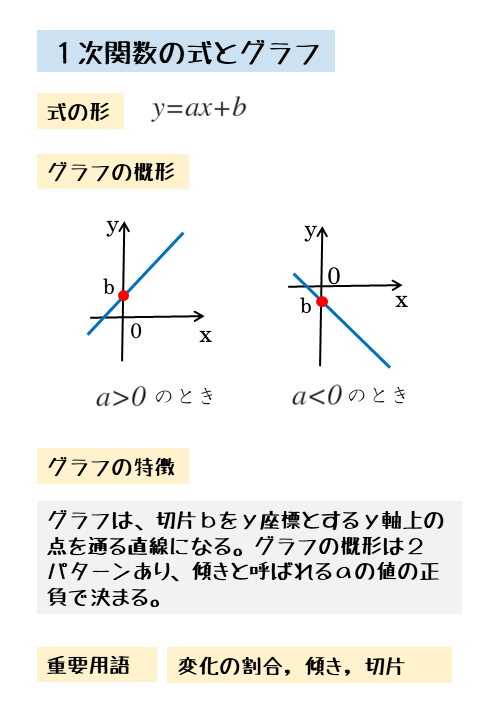
１次関数のグラフの概形と特徴

比例のグラフを上下に平行移動したような直線
比例定数ａの正負で右上がりか右下がりかが決まる
ａ＞０のとき、右上がりの直線
ａ＜０のとき、右下がりの直線
グラフはｙ軸と点(０，ｂ)で交わる

１次関数の式では「傾き」や「切片」のように独特の用語がいくつか出てきます。グラフと対応した用語なので、式とグラフを関連付けながら覚えましょう。

変化の割合

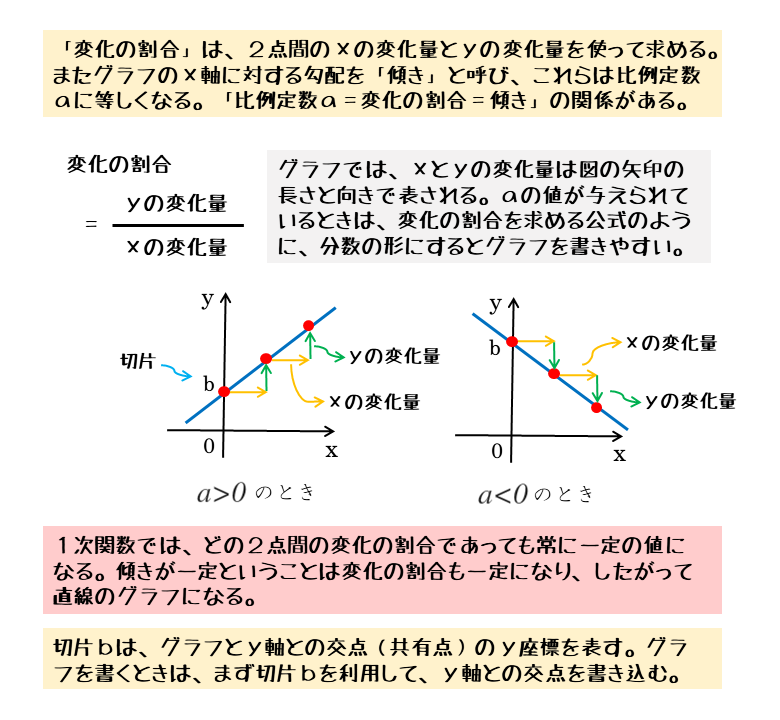
変化の割合は、変数ｘの値が１だけ変化するとき、変数ｙがどれだけ変化するのかを表す量で、以下のような式で表されます。

１次関数の変化の割合

\begin{align*} \quad \text{変化の割合} = \frac{\text{$y$ の増加量}}{\text{$x$ の増加量}} \end{align*}

ｘの増加量やｙの増加量は、２組の変数ｘ，ｙの値、言い換えると２点の座標を用いて求めます。具体例を挙げると以下の通りです。

変化の割合を求める

$1$ 次関数のグラフが

\begin{align*} \quad (1 \ , \ 2) \ , \ (3 \ , \ 5) \end{align*}

を通るときの変化の割合を求める。

\begin{align*} &\begin{array}{c|ccc} x & 1 & \longrightarrow & 3 \\ \hline y & 2 & \longrightarrow & 5 \\ \end{array} \end{align*}

$x$ の増加量は

\begin{align*} \quad 3-1=2 \end{align*}

$y$ の増加量は

\begin{align*} \quad 5-2=3 \end{align*}

よって、変化の割合は

\begin{align*} \quad \frac{5-2}{3-1}=\frac{3}{2} \end{align*}

これは $1$ 次関数のグラフの傾きに等しい。

２点の座標は(１，２)，(３，５)です。ｘの値が１から３に変化するとき、ｙの値は２から５に変化します。このときの増加量から、変化の割合を求めることができます。

このようにして得られる変化の割合は、傾きａの値に等しくなります。

ｘの増加量やｙの増加量のように「増加量」という言葉を用いているが、必ずしも増加するわけではない。増加というよりも「変化」と捉えておこう。

傾き

傾きは、１次関数や比例などの直線のグラフで用いられる用語で、直線がｘ軸に対してどのくらいの勾配（傾き具合）があるかを表します。

直線のｘ軸に対する勾配は、ｘの増加量１に対するｙの増加量で表されます。これは変化の割合のことです。ですから、傾きは変化の割合に等しくなります。

なお、１次関数の傾きはつねに一定で変化しません。また、どの２点の座標を用いても変化の割合は一定です。このような関係から、傾きが分かれば変化の割合が分かり、変化の割合が分かれば傾きが分かります。

１次関数のグラフを図示するには、傾きの情報が必要ですが、変化の割合から傾きを求めます。

１次関数では、比例定数ａ＝（変化の割合）＝（傾き）の関係がある。変数ｘ，ｙの値の変化を考えていれば変化の割合、グラフの勾配を考えているときは傾きを指すが、ほとんど区別せずに使っていることが多い。

１次関数の変化の割合と傾きの関係をまとめると以下のようになります。

切片

１次関数の式において、ｂのことを切片と言います（ｙ切片と言うときもある）。ｘ＝０のときのｙの値です。

また、グラフでは、切片ｂはグラフとｙ軸との交点のｙ座標を表します。

定数ａ，ｂの値は、傾きと切片に対応している。これらを上手に利用してグラフを手早く描くことができる。

１次関数のグラフを描くコツは以下のようになります。

１次関数のグラフを描くコツ

ｙ軸上に、切片ｂがｙ座標となる点を作る。
変化の割合ａを分数に戻す。整数のときは分母が１の分数で良い。負の数のときは分子にマイナスを移動。
１で作った点から、分母（ｘの増加量）のぶんだけ右に移動し、分子（ｙの増加量）のぶんだけ上（または下）に移動し、そこに点を作る。上下の移動は分子の符号で決まる。
作った２点を通る直線を引く。

直線のグラフを図示するには２点あれば十分です。傾きと切片の情報から２点を作りましょう。

２乗に比例する関数の式とグラフ

変数ｘ，ｙが、ｙ＝ａｘ²という式で表される関係のとき、２乗に比例する関係にあると言います。文字ａは、変数ではなく定数で、比例定数と言います。

２乗に比例する関係では、変数ｙは変数ｘの２次式で表されます。

なお、２乗に比例する関数のことを、高校数学では２次関数と言います。

２乗に比例する関係にあるとき、グラフの概形や特徴は以下のようになります（図も参考にして下さい）。

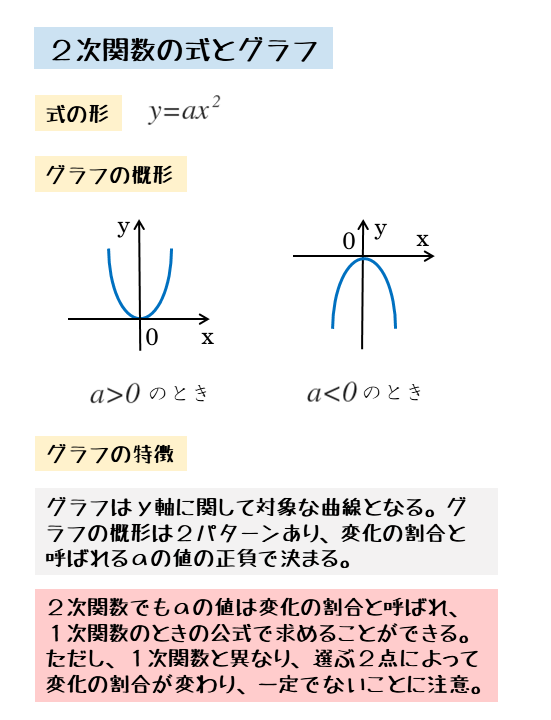
２乗に比例するグラフの概形と特徴

原点を通る曲線（放物線と言う）
ｙ軸に関して線対称なグラフ
ａ＞０のとき、下に凸の放物線
ａ＜０のとき、上に凸の放物線

中学数学では、「下に凸」のことを「上に開く」、「上に凸」のことを「下に開く」と表現します。最初のうちは混乱するでしょうが、少しずつ慣れていきましょう。

２乗に比例する関数の変化の割合

比例定数ａは、１次関数と同じく「変化の割合」と呼ばれますが、少し様子が異なります。

２乗に比例する関数では、変化の割合は基本的に一定になりません。グラフが直線でなく、曲線であることを考えれば、つねに一定でないことが分かります。グラフが曲線なのは、変化の割合が一定ではなく変化するからです。

２乗に比例する関数では、基本的に（変化の割合）≠（比例定数ａ）となる。変化の割合は、変数ｘ，ｙの増加量から求めよう。

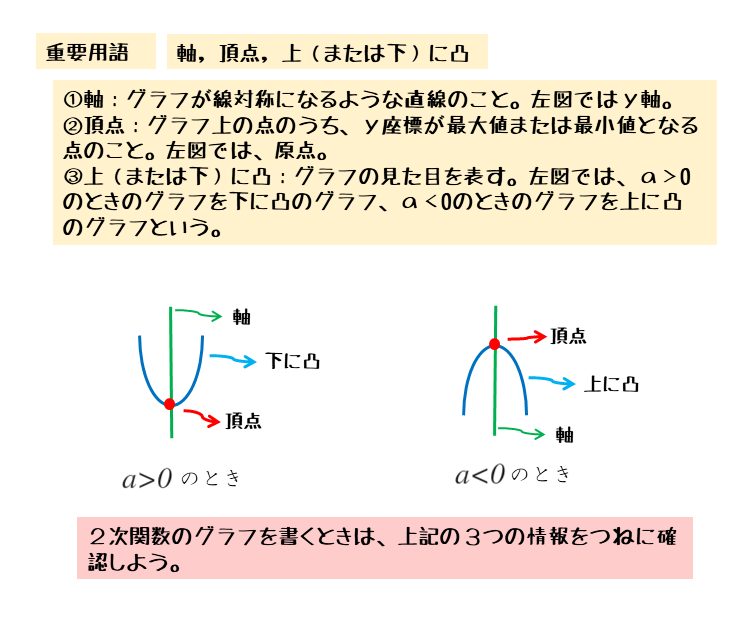
グラフの軸・頂点・凸

２乗に比例する関数は、高校では「２次関数」と言います。２次関数では、軸・頂点・凸の向きの情報を式から読み取り、それをもとにグラフを描きます。

２次関数を扱うとき、グラフの軸・頂点・凸の向きが式の何と対応するのかをしっかり把握できるようにしましょう。

関数では変数ｘ，ｙをセットで扱う

関数は２つの変数ｘ，ｙの関係を表すので、変数ｘ，ｙをつねにセットにして扱うことが大切です。

関数の式から、変数ｘとそれに対応する変数ｙを１組にして、点の座標とします。その座標をもとに点を作っていくと、関数のグラフになります。ですから、グラフを図示するには、変数ｘ，ｙの値が組になっていなければなりません。

また、グラフ上の点であれば、関数の式を満たすことが分かります。グラフ上の点の座標は、関数の式から得られるからです。これはとても大切な性質なので忘れないようにしましょう。

（グラフ上の点である）⇔（関数の式に座標を代入すると、等式が成り立つ）

色々な関数とグラフがありますが、式だけでは足りないし、グラフだけでも足りないので、お互いに補完し合う関係にあると言えます。

関数を上手に扱うために、式とグラフの両方を意識しながら考える習慣をつけましょう。

Recommended books

関数を上手に扱えるようになると、高校での数学はとてもラクになると思います。中学でも関数を扱いましたが、方程式や不等式との関係までは学習していません。

関数単体でなら何とかなっていても、方程式や不等式との関係性を理解しないと、高校では厳しくなります。逆に関係性が掴めれば、今までの苦労が何だったのかと思えるようになるでしょう。

関数は、たとえば物理の直線運動でもｖ－ｔグラフなどで登場するので、ぜひとも攻略しておきたい単元です。

オススメその１

１冊目に紹介するのは『おもしろいほどよくわかる高校数学関数編』です。図解してあるので、関数に苦手意識がある人でも読みやすいでしょう。

高校数学で学ぶ２次関数・指数関数・対数関数・三角関数について、その関数が生まれた身近な現象から説明し、それぞれの関数の性質を考える過程に多くのページを割きました。

書籍の紹介にもあるように、身近な現象を例に挙げて話が進むので、イメージしやすいかと思います。興味のある人は一読してみてはいかがでしょうか。

おもしろいほどよくわかる高校数学関数編

created by Rinker

オススメその２

２冊目に紹介するのは『改訂版坂田アキラの２次関数が面白いほどわかる本』です。

『おもしろいほどよくわかる高校数学関数編』は読み物に近いですが、こちらはより日常学習で利用しやすい教材です。

高校数学の基幹分野である「２次関数」は坂田の解説でマスターせよ！
累計５０万部超の「坂田理系シリーズ」の「２次関数」。２００９年４月に刊行した「新装版」の新課程版。学習者がつまずきやすい「場合分け」の丁寧な解説が最大の特長。基本から応用、重要公式からテクニックまで、幅広く網羅した「２次関数」対策の決定版！！旧版になかった「解の配置」のテーマを増設。

教科書で理解できない箇所があっても本書が補助してくれるでしょう。そういう意味では基礎レベルなので、予習や復習のときに教科書とセットで利用するのが良いでしょう。