中学数学｜正負の数の加減算について

09/25/2021中学数学

正負の数の減算

次の減算について、数直線を利用して言葉に置き換えてみます。

例題

次の計算をせよ。

\begin{align*} &\quad 5. \quad \left(+1 \right)-\left(+3 \right) \\[ 7pt ] &\quad 6. \quad \left(+1 \right)-\left(-3 \right) \end{align*}

減算の式を言葉で考えるとき、減算（減法）の計算記号マイナス（－）は、「引く」「減じる」「戻る」などの言葉に置き換えます。

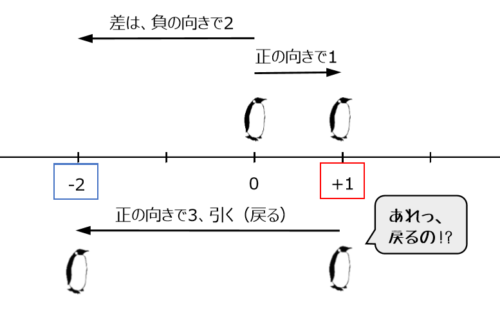
注目したいのは、符号の指定する向きと点の実際の動きとの違いです。５番目の式では以下のようになります。

正の向きに絶対値が１である＋１に対応する点に対して、
正の向きを向いて、絶対値が３のぶんだけ戻す（＝引く）と、
その結果、＋１に対応する点は－２対応する点に移動した。

例題５の計算結果

\begin{align*} \quad &\left(+1 \right)-\left(+3 \right) \\[ 7pt ] = \ &-2 \end{align*}

正負の数の減算が面白くて難しいのは、減算のために引く、言い換えると戻す必要があるので、符号が示す向きとは逆向きに進んでしまうところです。

正負の数の減算では、結果的に符号の示す向きとは逆向きに進める。

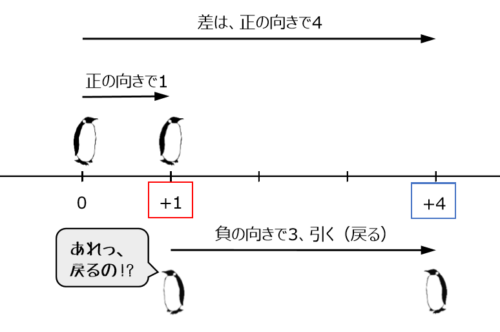
６番目の減算も同様に考えると、以下のようになります。

正の向きに絶対値が１である＋１に対応する点に対して、
負の向きを向いて、絶対値が３のぶんだけ戻す（＝引く）と、
その結果、＋１に対応する点は＋４対応する点に移動した。

例題６の計算結果

\begin{align*} \quad &\left(+1 \right)-\left(-3 \right) \\[ 7pt ] = \ &+4 \end{align*}

今度は負の向きを指定されましたが、結果としては逆向きに進んだことになります。

減算から分かるルール

正負の数の減算では、どんな規則性が見られるのか考えてみます。

符号が指定する向きと、実際の移動の向きとを表す部分に下線を引いてみます。

符号と減算記号に注目

\begin{align*} &\quad 5. \quad \left(+1 \right) \underline{-}\left(\underline{+}3 \right) \\[ 7pt ] &\quad 6. \quad \left(+1 \right) \underline{-}\left(\underline{-}3 \right) \end{align*}

下線部分だけを、言葉に置き換えてみます。減算記号と数の符号との組み合わせで違いがあります。

例題５の－(＋３)

正の向きを向いて、引く（戻す）＝正の向きと逆向きに進める＝負の向きに進める（足す）

例題６の－(－３)

負の向きを向いて、引く（戻す）＝負の向きと逆向きに進める＝正の向きに進める（足す）

このように減算は言葉を用いると、加算を使った表現に置き換えることができます。

減算を加算に置き換えるには、減算の計算記号の後ろにある符号に注目。

式で書き換えると以下のようになります。

減算から加算へ

例題５正の向きを向いて戻る ⇒ 負の向きを向いて進む

\begin{align*} \quad &\left(+1 \right) \underline{-}\left(\underline{+}3 \right) \\[ 7pt ] = \ &\left( +1 \right) \underline{+}\left(\underline{-}3 \right) \\[ 7pt ] = \ &-2 \end{align*}

例題６負の向きを向いて戻る ⇒ 正の向きを向いて進む

\begin{align*} \quad &\left(+1 \right) \underline{-}\left(\underline{-}3 \right) \\[ 7pt ] = \ &\left(+1 \right) \underline{+}\left(\underline{+}3 \right) \\[ 7pt ] = \ &+4 \end{align*}

例題５，６から分かるのは、減算を加算に置き換えることができるということです。正の数を引くのであれば、負の数を加えれば良く、負の数を引くのであれば、正の数を加えれば良いとなります。

正負の数の減算では、「正の数を引く」は「負の数を足す」、「負の数を引く」は「正の数を足す」ことに等しい。

加減算を加算に統一するメリット

減算を加算で表せることで、正負の数の加減算はすべて加算に統一できます。そのメリットは非常に大きいです。

計算がすべて加算であれば、交換法則と結合法則を利用できるようになります。それに、多項式であれば、加算の計算記号やカッコを省略して、簡略化した表記もできます。

先ほどの加減算で、加算の計算記号やカッコを省略すると、以下のようになります。

カッコの省略

\begin{align*} 1. \quad &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+1+3 \\[ 15pt ] 2. \quad &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &+1-3 \\[ 15pt ] 3. \quad &\left(-3 \right)+\left(+1 \right) \\[ 7pt ] = \ &-3+1 \\[ 15pt ] 4. \quad &\left(-1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-1-3 \\[ 15pt ] 5. \quad &\left(+1 \right)-\left(+3 \right) \\[ 7pt ] = \ &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &+1-3 \\[ 15pt ] 6. \quad &\left(+1 \right)-\left(-3 \right) \\[ 7pt ] = \ &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+1+3 \end{align*}

加算の計算記号や数のカッコを省略した式では、加算する数を横に並べただけの表記になっています。

計算記号と符号が混在する式よりも、符号だけの式の方が扱いやすい。

正負の数を加減算するときの手順

正負の数の加減算を行うとき、基本的には以下のような手順で計算します。

正負の数を加減算するときの手順

加減算を加算に統一する。
加算の計算記号（＋）とカッコを省略して、式を簡略化する。
加算の規則性を利用して、加算後の符号と絶対値を別々に求める。

手順に沿って計算すると、以下のようになります。

加減算の手順に沿って計算

\begin{align*} 1. \quad &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+1+3\\[ 7pt ] = \ &+\left(1+3 \right) \\[ 7pt ] = \ &+4 \\[ 15pt ] 2. \quad &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &+1-3\\[ 7pt ] = \ &-\left(3-1 \right) \\[ 7pt ] = \ &-2 \\[ 15pt ] 3. \quad &\left(-3 \right)+\left(+1 \right) \\[ 7pt ] = \ &-3+1 \\[ 7pt ] = \ &-\left(3-1 \right) \\[ 7pt ] = \ &-2 \\[ 15pt ] 4. \quad &\left(-1 \right)+\left(-3 \right) \\[ 7pt ] = \ &-1-3\\[ 7pt ] = \ &-\left(1+3 \right) \\[ 7pt ] = \ &-4 \\[ 15pt ] 5. \quad &\left(+1 \right)-\left(+3 \right) \\[ 7pt ] = \ &\left(+1 \right)+\left(-3 \right) \\[ 7pt ] = \ &+1-3\\[ 7pt ] = \ &-\left(3-1 \right) \\[ 7pt ] = \ &-2 \\[ 15pt ] 6. \quad &\left(+1 \right)-\left(-3 \right) \\[ 7pt ] = \ &\left(+1 \right)+\left(+3 \right) \\[ 7pt ] = \ &+1+3 \\[ 7pt ] = \ &+\left(1+3 \right) \\[ 7pt ] = \ &+4 \end{align*}

上述の計算過程はかなり丁寧に記述しています。ですから、実際にはここまで記述することはありません。

加減算の規則性に慣れてくると、手順のいくつか、特に１，２番目の過程を飛ばせるようになります。

いくつかの手順を省略した計算過程は以下のようになります。これくらいの計算過程が適切です。

加減算の手順を短縮して計算

\begin{align*} 1. \quad &\left(+1 \right) \underline{+}\left(\underline{+}3 \right) \\[ 7pt ] = \ &+1\underline{+}3\\[ 7pt ] = \ &+4 \\[ 15pt ] 2. \quad &\left(+1 \right) \underline{+}\left(\underline{-}3 \right) \\[ 7pt ] = \ &+1\underline{-}3\\[ 7pt ] = \ &-2 \\[ 15pt ] 3. \quad &\left(-3 \right) \underline{+}\left(\underline{+}1 \right) \\[ 7pt ] = \ &-3\underline{+}1 \\[ 7pt ] = \ &-2 \\[ 15pt ] 4. \quad &\left(-1 \right) \underline{+}\left(\underline{-}3 \right) \\[ 7pt ] = \ &-1\underline{-}3\\[ 7pt ] = \ &-4 \\[ 15pt ] 5. \quad &\left(+1 \right) \underline{-}\left(\underline{+}3 \right) \\[ 7pt ] = \ &+1\underline{-}3\\[ 7pt ] = \ &-2 \\[ 15pt ] 6. \quad &\left(+1 \right) \underline{-}\left(\underline{-}3 \right) \\[ 7pt ] = \ &+1\underline{+}3 \\[ 7pt ] = \ &+4 \end{align*}

このように規則性を上手に利用すると、計算過程が煩雑にならず、できる限り簡素に記述できます。

また、計算記号とカッコを省略した後は加算です。計算記号と符号を間違えないようにしましょう。

計算記号とその後ろの数の符号との組合せに規則性があることを利用する