図形と方程式|平面上の2点間の距離について

平面上の2点間の距離を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
問の解答・解説
平面上の2点間の距離を求めるために、公式に値を代入します。公式を利用するときには、文字に対応する値を正しく代入しましょう。
問の解答例 1⃣
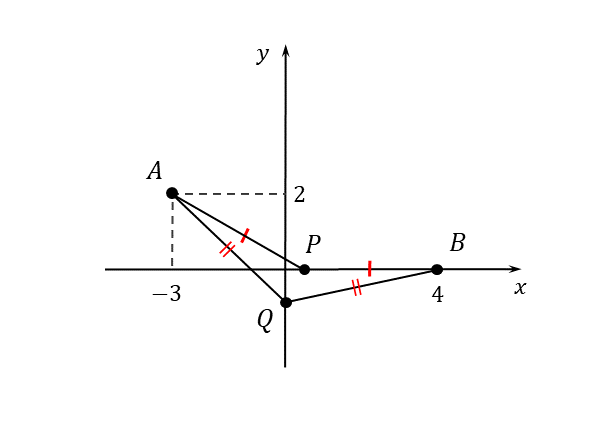
次に、軸上にあって、2点A,Bから等距離にある点を求めます。図示すると以下の通りです。
上手に作図できると、自分の解答が妥当かどうかを判断できます。これができると非常に有効なので、作図する習慣をつけましょう。
先にx軸上の点を求めます。x軸上の点の座標を自分で定義します。x軸上にある点のy座標はつねに0なので、定義するのはx座標です。
座標が定義出来たら、2点間の距離を利用して方程式を導きます。
問の解答例 2⃣
2点間の距離を用いて方程式を導くとき、公式をそのまま用いると根号が出てきます。根号が邪魔になるので、先に両辺を2乗しておくとスムーズに方程式を扱えます。
2点間の距離(公式)から方程式を導くとき、距離を2乗して根号を外しておこう。
最後に2点A,Bから等距離にあるy軸上の点を求めます。x軸上の点のときと同じ要領で解きます。
y軸上にある点のx座標はつねに0なので、定義するのはy座標です。座標が定義出来たら、2点間の距離を利用して方程式を導きます。
問の解答例 3⃣
公式に対応する値を正しく代入できれば、計算はそれほど難しくありません。ただ、符号ミスをしやすいので注意しましょう。符号ミスは習熟度が低いと起こりやすいので、たくさん演習をこなしておきましょう。
また、距離を2乗する解法は、軌跡やベクトルなどを扱った問題でもよく用いられます。しっかりマスターしておきましょう。
Recommended books
おすすめというよりも、個人的にちょっと気になる書籍を紹介します。気になる人はぜひ一読してみて下さい。
オススメ『NEW ACTION LEGENDシリーズ』
数学の参考書兼問題集と言えば、ほとんどの人が「チャート式」と答えるかもしれません。他には「Focus Gold(フォーカスゴールド)」も挙がるかもしれません。
おすすめに挙げた「NEW ACTION LEGENDシリーズ」は東京書籍から出版された教材です。チャートやフォーカスゴールドと同じくらい良い教材だと思います。個人的には本書の方が好きかもしれません。もともとは高校専用だったようですが、市販が解禁されています。
個人的に好感が持てるのは、数学的思考についての解説に紙面を割いているところです。解説も丁寧な感じがします。数学が得意な人にとっては、無意識にしていることなので、それほどありがたみのない情報かもしれません。ただ、苦手な人にとっては知らないことなので、とても貴重な情報だと思います。
新しい大学入試に対応するためには、思考力・表現力・判断力を日頃から養う必要があります。数学であれば、数学的な思考力です。数学的な思考をするために、日常学習で必要なことを身に付けられないと効率が良くありません。本書なら、そういったことを解決する助けになるかもしれません。
本書のサンプルが東京書籍のサイトにあります。雰囲気を掴めむことはできますが、詳しくは書店で確認すると良いでしょう。
系統性を重視し、思考力を磨く!
- 各例題には「思考のプロセス」(解答に至るまでの考え方)を示しています。
- 「条件の言い換え」「既知の問題に帰着」「具体的に考える」などのキーワードを挙げ、生徒に数学的思考法を意識させ、その後の問題解決において活用を促します。
- 既習例題との対比や試行錯誤の過程などを図解で示すことで、生徒に強く印象づけます。
- 途中を穴埋めにしたり、最後を質問で終えたりして、生徒に考える余地を残しています。
- 分野を越えて効果的な思考法(「逆向きに考える」「対称性」「動かす・固定する」など)について解説と例題で整理した「思考の戦略編」を、巻末に設けました。生徒の思考力を高めるとともに,入試への対応力をさらに一歩引き上げます。
- 例題の問題文をまとめた、本体から取り外せる小冊子「例題一覧」を設けました。問題の検索性が向上するとともに、問題集としての活用もしやすくなります。
- 各節冒頭の「まとめ」では,定義・定理・公式のまとめに加えて,「概要」を設けました。「概要」では、内容をイメージさせる解説をしたり、定理の証明の流れを示すとともに、大学入試における定理の証明問題の出題状況などを紹介したりしました。
さいごにもう一度まとめ
- 数直線上の2点間の距離は、座標の差を絶対値の記号で挟んでおこう。
- 平面上の2点間の距離は、数直線上の2点間の距離と三平方の定理との組み合わせで得られる。
- 座標の差は、大きい方から小さい方を引き算しよう。
- 距離から方程式を導くときは、距離を2乗して根号を外しておこう。
- 符号のミスに気を付けよう。