図形と計量｜三角比の定義について

07/26/2021数学１

三角比を定義しよう

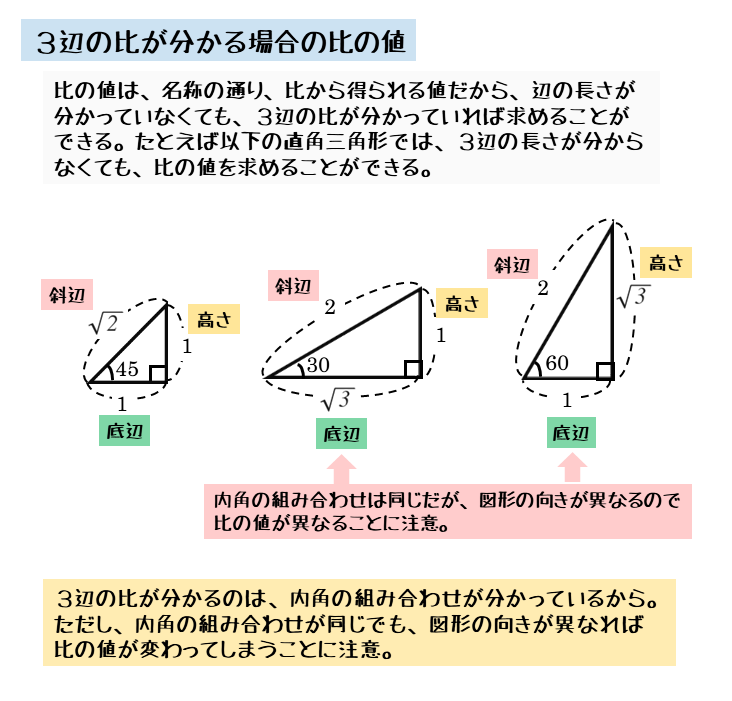
内角の１つが決まると、３辺の比が決まるので、三角比も決まります。しかし、三角比を求めたり、利用したりするとき、問題点が２つほど考えれらます。

三角比は、直角三角形の３辺のうち２辺から得られる値で３通りあります。ですから、どの２辺の組合せなのかを区別できなければなりません。

また、内角の組合せが同じでも図形の向きが異なると、高さと底辺の関係が逆になります。

その結果、三角比の値も異なってしまいます。これも区別できるようにする必要があります。

三角比を名称と角度で記号化して区別する

先ほどの問題点を解消するために、名称と角度を使って記号化することでそれぞれの三角比を区別します。

ここは三角比の定義に関わるので、正しく覚えることが大切です。また、図形の向きも重要なので、図形とセットにして覚えましょう。

内角が１つ決まれば三角比が決まるので、この内角に注目して三角比を定義します。

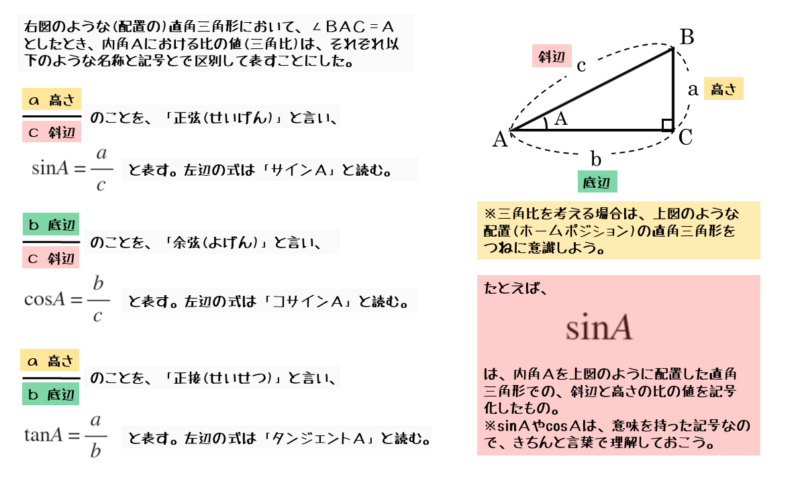
９０°の角を右側、注目する内角を左側に配置した直角三角形で３つの三角比を表します。このような配置の図形で求めた三角比をそれぞれ以下のように定義します。

それぞれの三角比を区別する呼び方や記号をしっかり覚えましょう。

三角比の定義

（高さと斜辺の比の値）＝（内角 $A$ に対する正弦）＝ $\sin A $

（底辺と斜辺の比の値）＝（内角 $A$ に対する余弦）＝ $\cos A $

（高さと底辺の比の値）＝（内角 $A$ に対する正接）＝ $\tan A $

ちなみに「ｓｉｎＡ」は「サインＡ」、「ｃｏｓＡ」は「コサインＡ」、「ｔａｎＡ」は「タンジェントＡ」と読みます。

注意したいのは、角度Ａまでを含めた「ｓｉｎＡ」を１つの記号として扱うことです。「ｓｉｎ」だけで記述しても意味を成しません。最初のうちは角度を書き忘れることがよくあるので注意しましょう。

このように１つの内角に注目して、ｓｉｎＡやｃｏｓＡなどの記号を使うことで、直角三角形の向きが決まり、どの２辺を選んで三角比を求めたのかも分かります。

三角比を実際の直角三角形で使ってみよう

良く用いられる三角比は、先ほど例に挙げた直角三角形の三角比です。

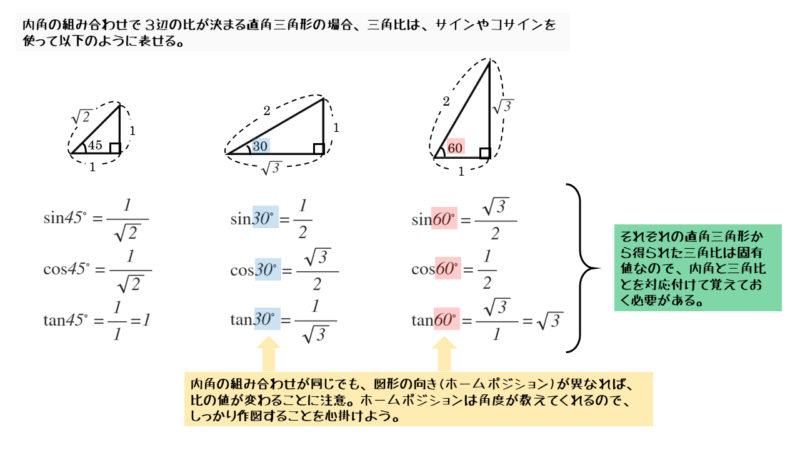
「４５°，４５°，９０°」や「３０°，６０°，９０°」などの直角三角形では、図形の大きさに関わらず、３辺の比がすでに分かっています。当然、辺比の値（三角比）も分かります。

今後は、これらの直角三角形の三角比を積極的に利用します。これらを記号化してみると以下のようになります。

三角比の値が同じでも、２辺の組合せや注目する内角が異なるので注意しましょう。

三角比の値が同じでも意味は異なる

値が同じでも、注目する内角が異なる

\begin{align*} &\quad \sin 30^{\circ} = \frac{1}{2} \\[ 7pt ] &\quad \cos 60^{\circ} = \frac{1}{2} \end{align*}

値が同じでも、$2$ 辺の組合せが異なる

\begin{align*} &\quad \sin 45^{\circ} = \frac{1}{\sqrt{2} } \\[ 7pt ] &\quad \cos 45^{\circ} = \frac{1}{\sqrt{2} } \quad \text{} \end{align*}

定義の直角三角形の配置を基本の位置として、三角比を求める習慣を付けましょう。つねに同じ配置であれば、２辺の組合せとその名称を覚えるのは簡単です。

Recommended books

図形の問題は、気付けないと全くと言って良いほど手も足も出なくなります。気付けるかどうかはやはり日頃から作図したり、図形を色んな角度から眺めたりすることだと思います。

そのためにもやはり演習量は大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。

演習をこなすとなると、単元別になった教材を使って集中的にこなすと良いでしょう。網羅型でも良いですが、苦手意識のある単元であれば、単元別に特化した教材の方が良いかもしれません。

オススメその１

分野ごとに押さえていくのに役立つのは『高速トレーニング』シリーズです。三角関数、ベクトル、数列などの分野もあります。

ここで紹介するのは『数学１高速トレーニング三角比編』です。

三角比に苦手意識のある人にとって、躓きやすいところを解説してあるので良い教材だと思います。基礎の定着に向いた教材です。

これで自信がついたら、チャートなどのもう少し難易度の高い問題を扱った教材に取り組むと良いでしょう。三角比は三角関数に関わるので、ここでしっかりマスターしておきましょう。

数学１高速トレーニング三角比編

created by Rinker

オススメその２

『改訂版坂田アキラの三角比・平面図形が面白いほどわかる本』もおすすめです。

計算過程が省略されず、丁寧に記述されているので、計算の途中で躓くこともほとんどないでしょう。苦手な人や初学者にとって良い補助教材になると思います。

坂田のビジュアル解説で最近流行りの空間図形までフォロー!

数学１「図形と計量」（いわゆる三角比）と数学Ａ「図形の性質」の基本事項をまとめ、それぞれの典型問題および融合問題の考え方・解き方がていねいに解説されています。

また、今回の改訂により、近年の大学入試（上位から下位まで幅広く）で頻出の空間図形の問題を厚くしました。