式と証明|3次式の展開について

今回から数学2「式と証明」について学習します。この章では、主に3次以上の式を扱います。
ここでは導入として、数学1でも扱った「3次式の展開」を学習します。公式がいくつか出てくるので、できるだけ早く使いこなせるように演習しておきましょう。
3次式について
3次式とは、項の中で最も高い次数が3となる式のことです。
たとえば、以下のような式を3次式と言います。
3次式の例
\begin{align*} &(1) \quad 2x^{3} \\[ 7pt ] &(2) \quad -xy^{2} + y^{2} – 1 \\[ 7pt ] &(3) \quad \left(x + y \right)^{3} \end{align*}例に挙げた(3)の式について、カッコの中の式は1次式なので、3次式に見えないかもしれません。
しかし、展開してみると最高次数が3となります。ですから3次式として扱います。ここでは、このような3次式の展開について学習します。
3次式の展開
3次式の展開では、数学1で学習した指数法則や乗法公式を利用します。すでに学習した乗法公式を上手に利用すれば、3乗以上であっても展開することができます。そのためにも2次式の乗法公式は必修です。
実際に3次式を展開してみましょう。
3次式の展開
\begin{align*} &\left(a + b \right)^{3} \\[ 10pt ] = \ &\left(a + b \right)\left(a + b \right)^{2}& &\text{(指数法則を利用)} \\[ 10pt ] = \ &\left(a + b \right)(a^{2} +2ab +b^{2} \ )& &\text{(乗法公式を利用)} \\[ 10pt ] = \ &a^{3} +2a^{2}b +ab^{2} + a^{2}b + 2ab^{2} +b^{3}& &\text{(分配法則を利用)} \\[ 10pt ] = \ &a^{3} +3a^{2}b +3ab^{2} + b^{3}& &\text{(同類項を整理)} \end{align*}このように指数法則や乗法公式を利用すれば、3次式を展開することができます。
ただ、毎回この展開を行うのは面倒です。ですから、3次式の展開の式として公式化されています。ここでは、これらの公式を3次式の乗法公式や展開公式と呼びます。
3次式の乗法公式その1
和の立方
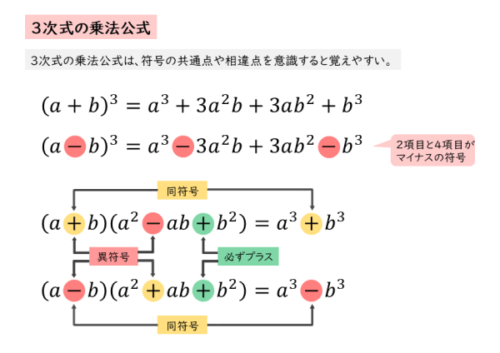
\begin{align*} \quad \left(a + b \right)^{3} = a^{3} +3a^{2}b +3ab^{2} +b^{3} \quad \cdots \text{①} \end{align*}差の立方
\begin{align*} \quad \left(a – b \right)^{3} = a^{3} -3a^{2}b +3ab^{2} -b^{3} \quad \cdots \text{②} \end{align*}一般に、①式は「和の立方」、②式は「差の立方」と言われます。
②式の「差の立方」については、①式の「和の立方」から導出できます。
「和の立方」から「差の立方」へ
①式の $b$ を $-b$ に置き換えると
\begin{align*} \quad \left\{a + (- b) \right\}^{3} &= a^{3} +3a^{2} \cdot (-b) +3a \cdot (-b)^{2} +(-b)^{3} \\[ 7pt ] \therefore \ (a \ – b)^{3} &= a^{3} -3a^{2}b +3ab^{2} -b^{3} \quad \cdots \text{②} \end{align*}①式と②式は、項の数や係数が似ているので、共通点や相違点を意識して覚えると良いでしょう。横に並べるよりも上下に並べた方が覚えやすいです。
また、3次式の展開の公式として、以下の式もあります。
3次式の乗法公式その2
立方の和
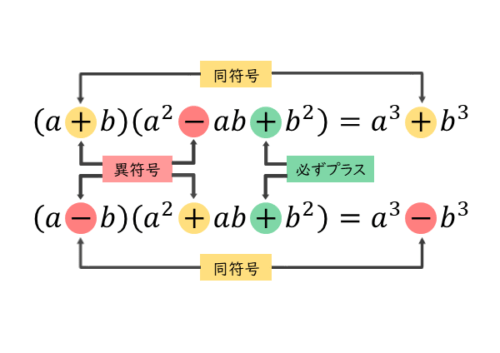
\begin{align*} \quad \left(a + b \right)\left(a^{2} -ab +b^{2} \right) = a^{3} +b^{3} \quad \cdots \text{③} \end{align*}立方の差
\begin{align*} \quad \left(a – b \right)\left(a^{2} +ab +b^{2} \right) = a^{3} -b^{3} \quad \cdots \text{④} \end{align*}一般に、③式は「立方の和」、④式は「立方の差」と言われます。
③式と④式も分配法則で展開すると導出できます。ただ、同類項を整理すると、ほとんどの項が消えてしまいます。実際に導出してみると分かります。
3次式の乗法公式その2の導出
\begin{align*} \quad &\left(a + b \right)\left(a^{2} -ab +b^{2} \right) \\[ 7pt ] = \ &a^{3} -a^{2}b +ab^{2} +a^{2}b -ab^{2} +b^{3} \\[ 7pt ] = \ &a^{3} +b^{3} \quad \cdots \text{③} \\[ 10pt ] \quad &\left(a – b \right)\left(a^{2} +ab +b^{2} \right) \\[ 7pt ] = \ &a^{3} +a^{2}b +ab^{2} -a^{2}b -ab^{2} -b^{3} \\[ 7pt ] = \ &a^{3} -b^{3} \quad \cdots \text{④} \end{align*}分配法則で展開すると、6つの項が出てきますが、そのうち4つの項は消えてしまいます。
消えてしまうと分かっている項を毎回記述するのは効率的とは言えません。ですから、公式に当てはめて計算した方が断然速いです。符号に注目すると覚えやすいです。
公式を上手に使いこなすには、公式の成り立ちを理解し、実際に使ってみることが大切です。
また、公式の成り立ちを理解するには、自分で導出してみることが一番です。ただの暗記で終わらせないようにしましょう。
公式の導出は必ず経験しておこう。また、公式を使いながら覚えよう。
次は、3次式の展開を扱った問題を実際に解いてみましょう。