数と式|二重根号について

今回は二重根号について学習しましょう。
平方根を扱ったものに二重根号があります。この二重根号を扱った問題も平方根とともに頻出です。
二重根号の扱い方にはコツがあるので、そのコツをしっかりマスターしましょう。
二重根号を外そう
二重根号とは、根号の中に根号があるような、根号が二重になった数や式のことです。分母の有理化と同じように、優先的に処理します。
どちらの根号を外すか?
二重根号があるとき、根号の重複を無くして、根号が1つだけの数や式に書き換えます。計算よりも先に行う作業です。計算するための準備と言っても良いでしょう。
根号の重複をなくすために、二重に重なった根号のうち、外側の根号を外します。この外側の根号を外すには、平方根の性質を利用します。
絶対値の記号を上手に扱う
平方根の性質についておさらいしておきましょう。
平方根の性質の1つ目は、根号の中で2乗の形ができれば、根号のない数や式で表せるというものです。
二重根号の外側の根号を外すには、式を2乗の形にすればよい。
ただし、$\sqrt{a}$ は根号の前に符号がないので、正の平方根です。この場合、根号がなくなっても正の数として扱わなければなりません。そのための絶対値の記号を忘れないようにしましょう。
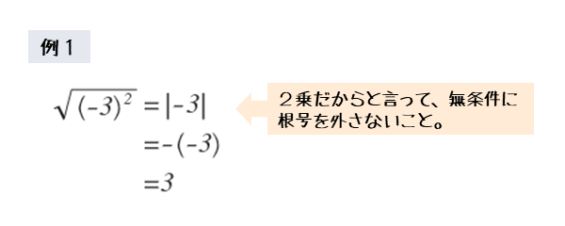
例1のように、絶対値の記号を外すときの基本の型は、単項式の場合で覚えましょう。
例1において、根号の前に符号がないので、与式は正の平方根です。根号を外した後も、正の数になっていることが分かります。
例2では、根号の中の式が単項式から多項式になっています。やや応用になりますが、多項式を1つの文字として扱えば、例1と同じように根号を外せます。
実際の計算では、根号を外した後、正負の判断をしてから絶対値の記号まで外します。多項式のときは間違えやすいので注意しましょう。
計算では、根号を外し、絶対値の記号を外すという2つのステップを踏む。また、例2で図解しているように、正負の吟味は、予め2乗の形を作るときにしておくと、絶対値の記号を外すときにラク。
乗法公式を利用して根号を外す
多項式が二重根号の中にあるとき、乗法公式を利用して多項式を因数分解します。因数分解することによって、2乗の形を作ります。
根号の中の多項式は、基本的に平方根を含む項と定数項の2つからなっています。そのような多項式を因数分解するために、展開の前後の式をよく見比べてみましょう。
平方根をもつ多項式と乗法公式
2項からなる多項式の2乗を展開するとき、乗法公式で展開することができました。
2項式の2乗の展開
\begin{align*} \quad \left(a+b \right)^{2} = a^{2} +2ab+b^{2} \end{align*}この乗法公式のa,bをそれぞれa,bの平方根に置き換えます。
2項式の2乗の展開
\begin{align*} \quad \left(a+b \right)^{2} = a^{2} +2ab+b^{2} \end{align*}ここで
\begin{align*} \quad a=\sqrt{a} \ , \ b=\sqrt{b} \end{align*}に置き換えると
\begin{align*} &\left(\sqrt{a}+\sqrt{b} \right)^{2} \\[ 7pt ] = \ &\left(\sqrt{a} \right)^{2} +2\sqrt{a}\sqrt{b}+\left(\sqrt{b} \right)^{2} \\[ 7pt ] = \ &a +2\sqrt{ab} +b \\[ 7pt ] = \ &\left(a+b \right) +2\sqrt{ab} \end{align*} \begin{align*} \therefore \ \left(a+b \right) +2\sqrt{ab} = \left( \sqrt{a}+\sqrt{b} \right)^{2} \quad \cdots \text{①} \end{align*}二重根号を外す問題では、①式の左辺が根号の中に入っています。この右辺を2乗の形(①の右辺)に変形することによって、外側の根号を外します。
①式の左辺が根号の中に入っている
\begin{align*} \quad \left(a+b \right) +2\sqrt{ab} = \left( \sqrt{a}+\sqrt{b} \right)^{2} \quad \cdots \text{①} \end{align*}この①式の左辺が根号の中に入ったものが二重根号の問題。
\begin{align*} \quad \sqrt{\left(a+b \right) +2\sqrt{ab}} \end{align*}この式の外側にある根号を外すには
\begin{align*} \quad \sqrt{\left(a+b \right) +2\sqrt{ab}}=\sqrt{\left( \sqrt{a}+\sqrt{b} \right)^{2}} \end{align*}と変形すれば良い。
因数分解するためには、数a,bが左辺と右辺でどのように対応しているのかを知っておく必要があります。
数a,bの関係
- ①式の左辺にあるa+bは、①式の右辺にある根号の中の数a,bの和
- ①式の左辺にあるabは、①式の右辺にある根号の中の数a,bの積
このような和と積の関係を利用して、数a,bの組合せを決めて因数分解します。
また、①式の左辺において、根号の前にある2も大切です。根号の前に2がないと、2乗の形に因数分解することができません。
まとめると以下のようになります。
次は、二重根号を扱った問題を実際に解いてみましょう。