図形の性質|角の二等分線と比について

比や角の二等分線を扱った問題を解いてみよう
次の問題を考えてみましょう。

最初のうちは慣れるために図が予め用意されていますが、センター試験などでは自分で作図しなければなりません。必要に応じて自分で作図するようにしましょう。
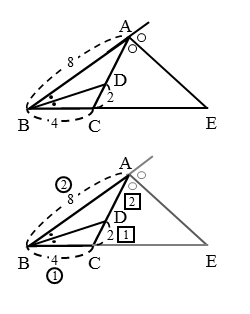
問(1)の解答・解説
問(1)
$\triangle ABC$ において、$AB=8 \ , \ BC=4$ とする。$\angle B$ の二等分線と辺 $AC$ の交点を $D$ とし、$\angle A$ の外角の二等分線と直線 $BC$ の交点を $E$ とする。$CD=2$ であるとき、次の線分の長さを求めよ。
線分 $AD$ の長さ
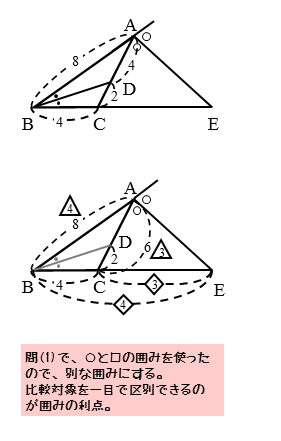
問題文を読みながら作図します。長さや比を書き込んでいくと、情報が多すぎて逆に見辛くなるときがあります。せっかく描いたのに良く分らない図になってしまうのは勿体ないです。
そうならないように、できるだけ大きな図を描いたり、必要な図だけを別途に抜き出したりしましょう。作図の仕方によって気付きが得られるかどうかが決まるので、よく考えて作図しましょう。
問(1)は、ADの長さを求める問題です。点Dができる原因になった∠Bの二等分線に注目します。
∠Bの二等分線に関わる箇所だけ抜き出した図を全体図と並べて描いておきます。内角の二等分線から得られる比の関係を書き込めば準備完了です。図形を扱った問題では、大半が作図で決まります。
内角の二等分線と比の関係から、以下の比例式が成り立ちます。
問(1)の解答例 1⃣
$\angle B$ の二等分線と比の関係より
\begin{align*} \quad BA : BC = AD : CD \end{align*}$AB=8 \ , \ BC=4$ より
\begin{align*} \quad AD : CD = 8 : 4 \end{align*}よって
\begin{align*} \quad AD : CD = 2 : 1 \end{align*}この比例式について、内項の積と外項の積の関係を利用すると、ADをCDで表すことができます。
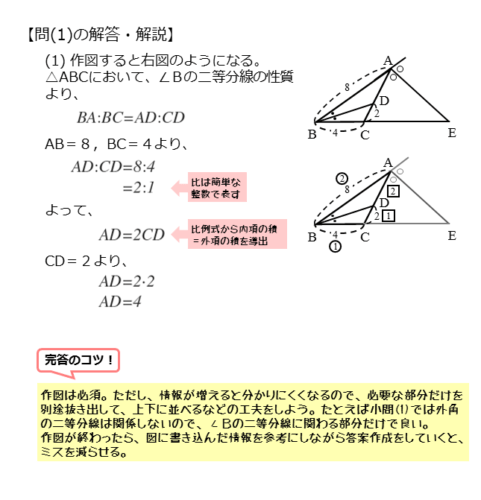
問(1)の解答例 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad AD : CD &= 2 : 1 \end{align*}これより
\begin{align*} \quad 1 \cdot AD &= 2 \cdot CD \\[ 5pt ] AD &= 2CD \end{align*}$CD=2$ より
\begin{align*} \quad AD = 2 \cdot 2 =4 \end{align*}問(1)のポイントと解答例をまとめると以下の通りです。
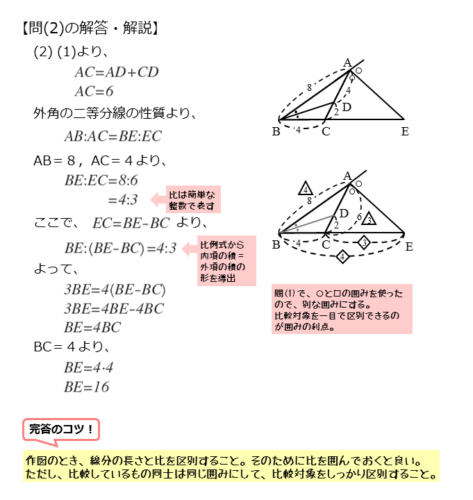
問(2)の解答・解説
問(2)
$\triangle ABC$ において、$AB=8 \ , \ BC=4$ とする。$\angle B$ の二等分線と辺 $AC$ の交点を $D$ とし、$\angle A$ の外角の二等分線と直線 $BC$ の交点を $E$ とする。$CD=2$ であるとき、次の線分の長さを求めよ。
線分 $BE$ の長さ
問(2)は、BEの長さを求める問題です。点Eができる原因になった∠Aの外角の二等分線に注目します。
∠Aの外角の二等分線に関わる箇所だけ抜き出して、別途に作図します。これと全体図を並べておくと良いでしょう。なお、全体図の方には、問(1)で得られた長さを忘れずに書き込んでおきます。
外角の二等分線から得られる比の関係を書き込めば準備完了です。
外角の二等分線と比の関係から、以下の比例式が成り立ちます。
問(2)の解答例 1⃣
$\angle A$ の外角の二等分線と比の関係より
\begin{align*} \quad AB : AC = BE : CE \end{align*}$AB=8 \ , \ AC=6$ より
\begin{align*} \quad BE : CE = 8 : 6 \end{align*}よって
\begin{align*} \quad BE : CE = 4 : 3 \quad \cdots \text{①} \end{align*}この比例式からBEの長さを求めたいところですが、CEの長さが不明です。ですから、この比例式だけではBEの長さを求めることができません。
ここで、長さが分かっているBCを利用します。
問(2)の解答例 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad BE : CE &= 4 : 3 \quad \cdots \text{①} \end{align*}これより
\begin{align*} \quad BE : BC = 4 : 1 \end{align*}よって
\begin{align*} \quad BE = 4BC \end{align*}これと①より
\begin{align*} \quad 4BC : CE = 4 : 3 \end{align*}よって
\begin{align*} \quad 4CE &=3 \cdot 4BC \\[ 7pt ] CE &=3BC \end{align*}$BC=4$ より
\begin{align*} \quad CE =12 \end{align*}比例式を導いただけでは求めることができないので、少し工夫が必要な問題でした。問(1)よりも難易度が高い問題です。
問(2)のポイントと解答例をまとめると以下の通りです。
比較対象が分かるように比を書き込みましょう。また、比の数字が同じでも、比較対象でなければ同じ囲みにしないように気を付けましょう。
入試レベルになると、1つの三角形の中に内角や外角の二等分線が混在した問題がよく出題されます。そんなときは1つの図だけで考えずに、必要に応じて別途に作図しましょう。
作図のコツを掴めば、解ける問題が増えるので、面倒臭がらずに取り組もう。
Recommended books
オススメその1
予習の際に理解が進めば授業のスピードについていくことができ、復習や課題をこなす時間も少なくて済みます。予習や復習の補助教材に向いている教材が『とってもやさしい数学』シリーズです。
とってもやさしい数学1・Aでは2冊とも中学で学習した内容にも触れており、中学内容と高校内容とのつながりを把握しやすい教材です。
一学期のうちは不安を抱えながら学習を進めていく人も多いかと思います。スタートで躓かないためにも易しく取り組みやすい教材を使うのも一つのやり方です。無理をして内容の難しい教材を使うよりもはるかに良いでしょう。
基礎的な内容を扱っているので、数学が苦手な人でも取り組みやすくなっています。興味のある人はぜひ一読してみて下さい。
『高校とってもやさしい数学1・A 改訂版 その1』は「数と式」「2次関数」の単元を扱っています。
『高校とってもやさしい数学1・A 改訂版 その2』は「場合の数」「確率」「整数の性質」「図形の性質」「三角比」の単元を扱っています。
オススメその2
『高校の数学I・Aが1冊でしっかりわかる本』は、これ1冊で数学1・Aの全範囲を復習できます。内容のレベルは「とってもやさしい」シリーズとそれほど変わらず、教科書レベルです。
本書と「とってもやさしい」シリーズのページ数を比較してみました。「とってもやさしい」シリーズは、1冊ごとのページ数が少ないのですが、分冊なのが難点です。
- 高校とってもやさしい数学1・A 改訂版 その1:175ページ
- 高校とってもやさしい数学1・A 改訂版 その2:189ページ
- 高校の数学I・Aが1冊でしっかりわかる本:192ページ
ページ数を比べると分かるように、本書の方が1冊でも遥かにページ数が少ないので、短時間でこなすことができます。
紹介した教材を使うとした場合、高校1年生であれば「とってもやさしい」シリーズで復習し、高校2,3年生であれば『高校の数学I・Aが1冊でしっかりわかる本』と「とってもやさしい」シリーズを組み合わせて復習すると良いでしょう。
こんな人に向いています
- 定期試験や大学受験のための基礎を固めて、成績を上げたい高校生へ。
- 医療看護系入試、高卒認定試験などの対策で、短期間で数学1・Aを理解したい方へ。
- 学び直しや頭の体操をしたい大人の方へ。
さいごに、もう一度、頭の中を整理しよう
- 内分点は線分上にある点。
- 外分点は線分の延長線上にある点で、2パターンある。
- 線分の長さを求めるために、比例式を立式しよう。
- 三角形の内角の二等分線では、対辺に内分点ができる。
- 三角形の外角の二等分線では、対辺に外分点ができる。