数と式｜平方根について

07/26/2021数学１

平方根を扱った問題を解いてみよう

次の問題を解いてみましょう。

平方根を扱った問題では、平方根の性質を利用して、平方根の形を変えることを優先しましょう。

問１の解答・解説

問１

$\begin{align*} \quad \sqrt{8}-\sqrt{32} \end{align*}$

問１は、２つの平方根の和を表しています。平方根の加減算は中学で学習したように、同類項の計算と同じようにします。もとは分配法則の逆を利用した計算です。

平方根の加減算では根号の中の数が同じであることが条件です。与式の平方根をそれぞれ変形します。

問１の解答例 1⃣

$\begin{align*} \quad \sqrt{8} &= \sqrt{{2}^{2} \times 2} \\[ 7pt ] &= 2 \sqrt{2} \\[ 10pt ] \quad \sqrt{32} &= \sqrt{{4}^{2} \times 2} \\[ 7pt ] &= 4 \sqrt{2} \end{align*}$

根号の中の数が揃えば２つの項を整理します。

問１の解答例 1⃣

$\begin{align*} \quad \sqrt{8}-\sqrt{32} &= 2 \sqrt{2}-4 \sqrt{2} \\[ 7pt ] &= -2\sqrt{2} \end{align*}$

問１のポイントと解答例をまとめると以下のようになります。

根号の中の数をできるだけ小さくするときのコツは以下のようになります。

根号の中の数をできるだけ小さくするコツ

根号の中の数を因数分解（または素因数分解）する。
因数分解するとき、４，９，１６などの平方数を使った積で表す。
根号がついていない数は、平方根の前に置く。

問２の解答・解説

問２

$\begin{align*} \quad \left(2+\sqrt{3} \right)\left(2-\sqrt{3} \right) \end{align*}$

問２は、次の乗法公式を利用する問題です。

乗法公式

$\begin{align*} \quad \left(a+b \right) \left(a-b \right) = a^2 -b^2 \end{align*}$

文字と数の対応関係を把握してから、乗法公式に当てはめて展開し、整理します。

問２の解答例

$\begin{align*} \quad \left(2+\sqrt{3} \right)\left(2-\sqrt{3} \right) &= 2^2-\left(\sqrt{3} \right)^2 \\[ 7pt ] &= 4-3 \\[ 7pt ] &= 1 \end{align*}$

問２のポイントと解答例をまとめると以下のようになります。

問３の解答・解説

問３

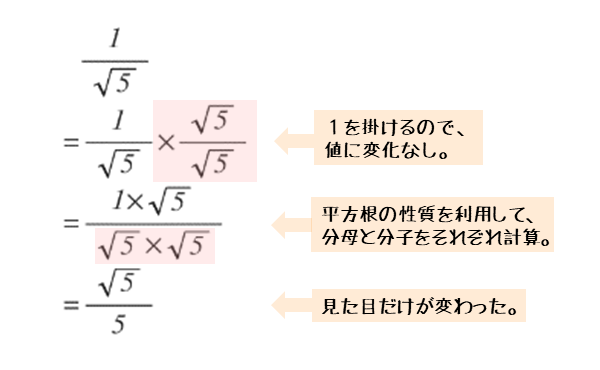
$\begin{align*} \quad \frac{1}{\sqrt{5}} \end{align*}$

問３は、分母を有理化する問題です。与式の分母に５の平方根があるので、これを根号がない形に変形するのが有理化です。

分母と分子にそれぞれ５の平方根を掛けます。このとき約分しないように気を付けましょう。掛ける前に戻ってしまいます。

分母と分子をそれぞれ乗算して整理します。整理した後であれば、約分して構いません。

問３の解答例

$\begin{align*} \quad \frac{1}{\sqrt{5}} &= \frac{1}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}} \\[ 7pt ] &= \frac{1 \times \sqrt{5}}{\sqrt{5} \times \sqrt{5}} \\[ 7pt ] &= \frac{\sqrt{5}}{5} \end{align*}$

問３のポイントと解答例をまとめると以下のようになります。

問４の解答・解説

問４

$\begin{align*} \quad \frac{1}{\sqrt{5}+2} \end{align*}$

問４も分母を有理化する問題です。問３と異なるのは、分母が単項式から多項式になったところです。

分母が多項式の場合、単項式である５の平方根を掛けたとしても、平方根が分母に残ってしまいます。このような場合には、先ほどの乗法公式を利用して分母を有理化します。

乗法公式

$\begin{align*} \quad \left(a+b \right) \left(a-b \right) = a^2 -b^2 \end{align*}$

この乗法公式を利用して、分母を有理化します。分母と分子をそれぞれ整理すると、有理化できます。

問４の解答例

$\begin{align*} \quad \frac{1}{\sqrt{5}+2} &= \frac{1}{\sqrt{5}+2} \times \frac{\sqrt{5}-2}{\sqrt{5}-2} \\[ 7pt ] &= \frac{1 \times \left(\sqrt{5}-2 \right)}{\left(\sqrt{5}+2 \right) \left(\sqrt{5}-2 \right)} \\[ 7pt ] &= \frac{\sqrt{5}-2}{\left(\sqrt{5} \right)^{\scriptsize{2}}-2^{\scriptsize{2}}} \\[ 7pt ] &= \frac{\sqrt{5}-2}{5-4} \\[ 7pt ] &= \sqrt{5}-2 \end{align*}$

入試で頻出なのは問４の計算です。単項式よりも多項式を有理化するパターンが多いので、確実に変形できるようにしておきましょう。

問４のポイントと解答例をまとめると以下のようになります。