図形と方程式｜円に切り取られる線分の長さについて

05/22/2021数学２

今回は、円によって切り取られる線分の長さについて学習しましょう。主に、円と直線を扱っているときに出てくる話題です。

円だけでなく、二等辺三角形や直角三角形などの性質も利用するので、図形の性質を確認しながら学習しましょう。

円を扱った問題は入試では頻出で、意外と難易度の高い問題が多いのが特徴です。何度も演習を重ねておきましょう。

円の中心から直線（弦）へ引いた垂線

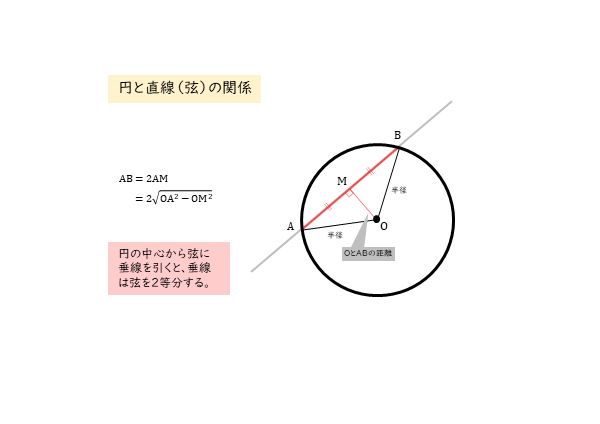
円と直線が異なる２点で交わるときを考えます。このとき、２つの共有点を結んだ線分のことを弦と言います。その弦に向けて円の中心から垂線を引くと、垂線は弦を２等分することが分かっています。

図のように、円の中心Ｏから弦ＡＢへ垂線を下ろし、その足をＭとします。

弦の両端Ａ，Ｂと円の中心Ｏを結んだ線分ＯＡ，ＯＢの長さは、円の半径に相当します。ですから、円の中心Ｏと２つの共有点Ａ，Ｂでできる△ＯＡＢは、二等辺三角形になります。

また、△ＯＡＢは、垂線ＯＭで２つの直角三角形（△ＯＡＭ，△ＯＢＭ）に分割されています。２つの直角三角形において、斜辺ＯＡ，ＯＢが円の半径に等しく、かつ垂線ＯＭが共通なので、斜辺と他の一辺がそれぞれ等しくなります。その結果、２つの直角三角形は合同となります。

２つの直角三角形が合同となるので、弦ＡＢが垂線ＯＭによって２等分されていることが分かります。

垂線が弦を２等分することの証明

$\begin{align*} &\text{$AB \perp OM$ より、$\triangle OAM$ と $\triangle OBM$ は直角三角形。} \\[ 5pt ] &\text{$\triangle OAM$ と $\triangle OBM$ において} \\[ 5pt ] &\quad OA=OB \quad \text{（円の半径）} \\[ 5pt ] &\quad OM \ \text{共通} \\[ 5pt ] &\text{となり、斜辺と他の一辺がそれぞれ等しいので、} \\[ 5pt ] &\quad \triangle OAM \equiv \triangle OBM \\[ 5pt ] &\text{よって、} \\[ 5pt ] &\quad AM=BM \\[ 5pt ] &\text{これより、垂線 $OM$ は弦 $AB$ を２等分する。} \end{align*}$

弦ＡＢに円の中心Ｏから垂線ＯＭを下ろしたとき、垂線ＯＭが弦ＡＢを２等分するので、それらの交点Ｍは弦ＡＢの中点となっています。

弦ＡＢの長さを求めるには、直角三角形を利用します。どちらかの直角三角形において、三平方の定理を利用すれば、弦の半分の長さ（ＡＭまたはＢＭの長さ）を求めることができます。そして、求めた長さを２倍すれば、弦ＡＢの長さとなります。

弦の長さ

$\begin{align*} &\text{$\triangle OAM$ において、三平方の定理より} \\[ 5pt ] &\quad AM= \sqrt{OA^{\scriptsize{2}}-OM^{\scriptsize{2}}} \\[ 5pt ] &\text{となるので、弦の長さは} \\[ 5pt ] &\quad AB=2AM=2 \sqrt{OA^{\scriptsize{2}}-OM^{\scriptsize{2}}} \end{align*}$

この弦の長さが、円と直線が異なる２点で交わるときに円によって切り取られる線分の長さとなります。

以上を踏まえて、例題を解いてみましょう。

円が直線から切り取る線分の長さを求めてみよう

例題

円

$x^{\scriptsize{2}}+y^{\scriptsize{2}}=16$ が直線

$y=x+2$ から切り取る線分の長さを求めよ。

図形を扱った問題なので、計算だけで済ませるのではなく、作図してから考えましょう。

例題の解答・解説

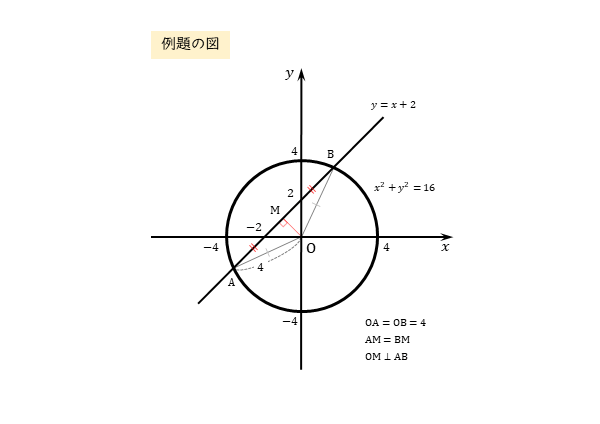
図示すると以下のようになります。

円と直線が異なる２点で交わっています。２つの交点をＡ，Ｂとします。また、円の中心から弦ＡＢに垂線を下ろし、その足をＭとします。点Ｍは弦ＡＢの中点です。

たとえば、△ＯＡＭにおいて三平方の定理を利用するためには、少なくとも線分ＯＡ，ＯＭの長さを必要とします。線分ＯＡの長さは、円の半径からすぐに分かります。

線分ＯＭの長さについては、円の中心と直線の距離に等しいことを利用します。点と直線の距離の公式に代入して求めます。

例題の解答例 1⃣

円と直線の交点を

$A \ , \ B$ とし、線分

$AB$ の中点を

$M$ とする。

線分

$OM$ の長さは、円の中心

$(0 \ , \ 0)$ と直線

$y=x+2$ の距離に等しいので、

$\begin{align*} \quad OM= &\frac{|0-0+2|}{\sqrt{ 1^{\scriptsize{2}}+(-1)^{\scriptsize{2}} }} \\[ 5pt ] = &\sqrt{2} \end{align*}$

また、円の半径は

$4$ である。

これで直角三角形の２辺の長さが揃いました。あとは弦の長さを求めるだけです。

例題の解答例 2⃣

$\begin{align*} &\quad \vdots \\[ 5pt ] &\text{$OA=4 \ , OM=\sqrt{2}$ より} \end{align*}$

$\begin{align*} \quad AB &= 2AM \\[ 5pt ] \quad &= 2\sqrt{OA^{\scriptsize{2}}-OM^{\scriptsize{2}}} \\[ 5pt ] \quad &= 2\sqrt{4^{\scriptsize{2}}-\left(\sqrt{2} \right)^{\scriptsize{2}}} \\[ 5pt ] \quad &= 2\sqrt{14} \end{align*}$

円の中心から弦へ引いた垂線は、弦の垂直２等分線となることを忘れないようにしましょう。また、点と直線の距離の公式も使いこなせるようにしておきましょう。

円の中心から弦に引いた垂線は、弦を垂直に２等分する。

点と直線の距離の公式において、円の中心が原点の場合、分子のｘ，ｙに代入する値は０なので、分子には直線の切片しか残りません。ですから、以下の式の方が使いやすいでしょう。

原点と直線の距離

原点と直線

$ax+by+c=0$ の距離

$d$ は

$\begin{equation*} \quad d=\frac{|c|}{\sqrt{a^{\scriptsize{2}}+b^{\scriptsize{2}} } } \end{equation*}$

例題の別解１

上述の解答例では、図形的に解きましたが、別解では、円と直線の交点の座標を利用して解きます。

円と直線の方程式を連立させて解けば、交点のｘ座標を求めることができます。ｘ座標が分かれば、ｙ座標も分かります。交点の座標が分かれば、２点間の距離の公式から弦の長さを求めることができます。

ここで注意したいのは、交点の座標を求めると言いましたが、厳密には座標を求めるわけではないということです。求めるのは、２つの交点のｘ座標の和と積です。

２点間の距離の公式には、２つの交点のｘ座標の和と積を代入します。この解法であれば、交点のｘ座標を直接求める必要がないので、計算がだいぶ楽になります。

例題の別解例１

直線の方程式を円の方程式に代入して整理すると

$\begin{align*} &\quad x^{\scriptsize{2}}+(x+2)^{\scriptsize{2}}=16 \\[ 5pt ] &\quad 2x^{\scriptsize{2}}+4x-12=0 \\[ 5pt ] &\quad x^{\scriptsize{2}}+2x-6=0 \ \cdots \text{①} \end{align*}$

①の実数解を

$\alpha \ , \ \beta$ とすると、解と係数の関係から

$\begin{align*} &\quad \alpha + \beta =-2 \\[ 5pt ] &\quad \alpha \beta =-6 \\[ 5pt ] &\text{円と直線の交点の座標は} \\[ 5pt ] &\quad (\alpha \ , \ \alpha+2) \ , \ (\beta \ , \ \beta+2) \\[ 5pt ] &\text{であるから、求める線分の長さは} \\[ 5pt ] &\qquad \sqrt{ (\beta-\alpha)^{\scriptsize{2}} +\bigl\{(\beta+2)-(\alpha+2) \bigr\}^{\scriptsize{2}} } \\[ 5pt ] &\quad =\sqrt{ 2(\beta-\alpha)^{\scriptsize{2}} } \\[ 5pt ] &\quad =\sqrt{ 2\bigl\{ (\beta+\alpha)^{\scriptsize{2}}-4\alpha \beta \bigr\} } \\[ 5pt ] &\quad =\sqrt{ 2\bigl\{ (-2)^{\scriptsize{2}}-4 \cdot (-6) \bigr\} } \\[ 5pt ] &\quad =2\sqrt{14} \end{align*}$

解と係数の関係は入試でも頻出です。線分の長さだけでなく、定積分などでも利用されます。また、乗法公式を応用しないと式変形できません。式の値を扱った問題では頻出なので、しっかり覚えておきましょう。

乗法公式の応用

$\begin{align*} (\beta-\alpha)^{\scriptsize{2}}= \ &{\beta}^{\scriptsize{2}}-2\alpha \beta+{\alpha}^{\scriptsize{2}} \\[ 5pt ] = \ &{\beta}^{\scriptsize{2}}+2\alpha \beta+{\alpha}^{\scriptsize{2}}-4\alpha \beta \\[ 5pt ] = \ &(\beta+\alpha)^{\scriptsize{2}}-4\alpha \beta \\[ 5pt ] \therefore \ (\beta-\alpha)^{\scriptsize{2}}= \ &(\beta+\alpha)^{\scriptsize{2}}-4\alpha \beta \end{align*}$

例題の別解２

もう１つ別解があります。相似を利用した解法です。

弦は直線上の線分なので、２点間の距離で求めることはできます。しかし、２つの交点のｘ座標が整数などの簡単な数で得られそうにない場合、この解法や別解１が役に立ちます。

弦を斜辺とし、ｘ，ｙ軸に平行な辺をもつ直角三角形が、直線の傾きをもとにした直角三角形と相似の関係にあることを利用します。

別解１と異なるのは、２つの交点のｘ座標を必要とするところです。しかし、この解法でもｙ座標を必要としないので、２点間の距離のときよりも計算が楽になります。

相似を利用した解法

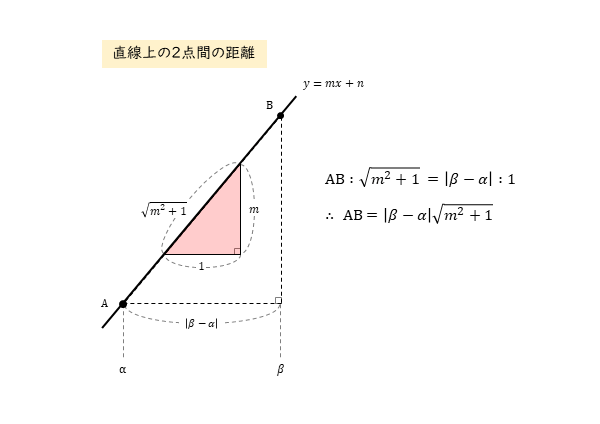
直線

$y=mx+n$ において、傾きが

$m$ であることから、

底辺

$1$ 、高さ

$m$ の直角三角形の斜辺の長さは

$\begin{equation*} \quad \sqrt{1^{\scriptsize{2}}+m^{\scriptsize{2}}} \end{equation*}$

と表せる。

直線

$y=mx+n$ 上の２点を

$A \ , \ B$ とし、その

$x$ 座標を

$\alpha \ , \ \beta$ とする。

このとき、線分

$AB$ の長さは

$\begin{align*} &\quad \left|\beta-\alpha \right| : 1 = AB : \sqrt{1^{\scriptsize{2}}+m^{\scriptsize{2}}} \\[ 5pt ] &\text{よって、} \\[ 5pt ] &\quad AB = \left|\beta-\alpha \right| \sqrt{1^{\scriptsize{2}}+m^{\scriptsize{2}}} \end{align*}$

この解法を利用した解答例は以下のようになります。

例題の別解例２

直線の方程式を円の方程式に代入して整理すると

$\begin{align*} &\quad x^{\scriptsize{2}}+(x+2)^{\scriptsize{2}}=16 \\[ 5pt ] &\quad 2x^{\scriptsize{2}}+4x-12=0 \\[ 5pt ] &\quad x^{\scriptsize{2}}+2x-6=0 \ \cdots \text{①} \end{align*}$

ここで、①の実数解を

$\alpha \ , \ \beta$ とする。

①を解くと

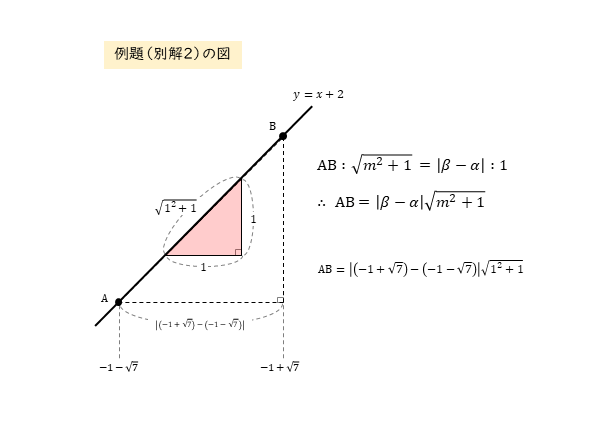
$\begin{align*} &\quad x=-1 \pm \sqrt{7} \\[ 5pt ] &\text{よって、} \\[ 5pt ] &\quad \alpha=-1 – \sqrt{7} \\[ 5pt ] &\quad \beta=-1 + \sqrt{7} \\[ 5pt ] &\text{とすると、求める線分の長さは} \\[ 5pt ] &\quad AB=\left| \left(-1 + \sqrt{7} \right)-\left(-1 – \sqrt{7} \right) \right| \sqrt{1^{\scriptsize{2}}+1^{\scriptsize{2}}} \\[ 5pt ] &\qquad \ =2\sqrt{7} \cdot \sqrt{2} \\[ 5pt ] &\therefore \ AB=2\sqrt{14} \end{align*}$

別解２の解法を利用することはほとんどないかもしれません。ただ、なかなか気付かない視点なので、このような考え方があることを知っておくと良いでしょう。

次は、円に切り取られる線分の長さを扱った問題を実際に解いてみましょう。

数学２円,距離,図形と方程式,弦

Posted by kiri

$数学を学習するときに実践したいこと$

数学を学習するときに実践したいことについて

図形と方程式｜円と直線の位置関係について

円と直線（弦）

円の中心から直線（弦）へ引いた垂線

円が直線から切り取る線分の長さを求めてみよう

例題の解答・解説

例題の別解１

例題の別解２