図形と方程式|円上の点における接線について

今回は、円上の点における接線について学習しましょう。
接線に関する問題は、入試でも頻出で、共通テストレベルから大学別の個別試験レベルまで様々です。
注意したいのは、単純な図形としてだけでなく、方程式などと絡めて出題されるということです。たとえば、接点のx座標を求める際には方程式を利用します。
分野をまたぐ融合問題のせいで意外と難易度が高いので、何度も演習を重ねておきましょう。
円の接線
原点を中心とする円の接線の方程式
前回の復習になりますが、円の接線の方程式を確認しておきましょう。ここで、接線は中心を原点とする円に接するとします。
円の接線の方程式
円 $x^{2}+y^{2}=r^{2}$ 上の点 $P(x_{1} \ , \ y_{1})$ における接線の方程式は
\begin{align} \quad x_{1} \ x+y_{1} \ y=r^{2} \end{align}ただし
\begin{align} \quad {x_{1}}^{2}+{y_{1}}^{2}=r^{2} \end{align}円の接線の方程式は、円の方程式に似ているので比較的覚えやすい式です。接線の方程式を求めるには、円の方程式と接点の座標の2つが必要です。
ここでのテーマは「円上の点における接線」ですが、中心が原点でない円の接線を対象としています。ですから、接線が分かっていたとしても、中心が原点以外であることに注意しましょう。
このとき接線の公式を利用できるのか気になるところです。残念ながらそのまま用いることはできません。
中心以外の点を原点とする円の接線の方程式は、以下のようになります。
円の接線の方程式(一般化)
円の方程式を
\begin{align} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \end{align}とする。
この円上の点 $P(x_{1} \ , \ y_{1})$ における接線の方程式は
\begin{align} \quad \left(x_{1}-a \right)\left(x-a \right)+\left(y_{1}-b \right)\left(y-b \right)=r^{2} \quad \cdots \text{①} \end{align}なお、$a=0 \ , \ b=0$ のとき
\begin{align} \quad x_{1} x + y_{1} y =r^{2} \end{align}となり、①式は原点を中心とする円の接線の方程式を含むことが分かる。
カッコの中の式が似ているので注意しましょう。一方は定数になりますが、他方は変数x,yが用いられているので、ちゃんと1次関数の式になります。
また、この公式(①式)は原点を中心とする円の接線の方程式も含むので、こちらの式を覚えておけば応用が利くでしょう。
この公式も覚えるのはそれほど難しくないでしょうが、導出の過程をきちんと把握しておきましょう。導出の過程ではこれまでに学習した事柄も出てきます。
この公式の導出については例題を用いて確認します。
円上の点における接線を求めてみよう
次の例題を解いてみましょう。
例題
中心が $(a \ , \ b)$ で、半径 $r$ の円がある。
この円上の点 $(x_{1} \ , \ y_{1})$ における接線の方程式は
\begin{align} \quad \left(x_{1}-a \right)\left(x-a \right)+\left(y_{1}-b \right)\left(y-b \right)=r^{2} \end{align}で表されることを示せ。
円の中心が原点でないことに注意しましょう。
例題の解答・解説
円の接線を求めるには、公式(原点中心の円の接線)を利用します。
ただ、与えられた円の中心は原点ではありません。ですから、接点の座標をこのまま公式に代入しても誤った使い方になってしまいます。
公式を上手く利用するには、円の中心が原点になければなりません。そのためにも与えられた円を平行移動します。
図形の平行移動が接線の方程式を求めるための大切な考え方になります。
与えられた円の方程式を導出し、中心が原点になるように平行移動します。
例題の解答例 1⃣
\begin{align} &\quad C \ : \ \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \\[ 7pt ] &\quad A \ : \ (x_{1} \ , \ y_{1}) \end{align}とする。
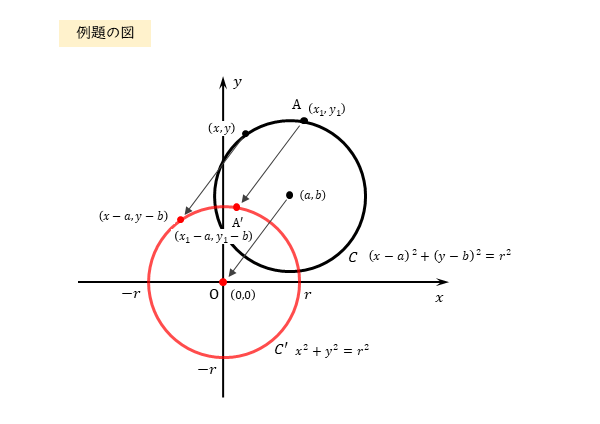
円 $C$ を中心 $(a \ , \ b)$ が原点 $(0 \ , \ 0)$ にくるように平行移動する。
平行移動後の円を $C’$ とすると、その方程式は
\begin{align*} \quad x^{2}+y^{2}=r^{2} \end{align*}となる。
平行移動によって、中心が原点になりました。それに伴い、接点の座標も変わっていることに注意しましょう。
点の平行移動
$x$ 軸方向に $-a$、$y$ 軸方向に $-b$ だけ平行移動すると、点 $(x \ , \ y)$ は点 $(x-a \ , \ y-b)$ に移る。
中心が原点に移りました。接点の座標を公式に代入すれば、接線の方程式を求めることができます。
例題の解答例 2⃣
\begin{align} &\quad \vdots \\[ 7pt ] \quad &x^{2}+y^{2}=r^{2} \\[ 7pt ] &\quad \vdots \end{align}この平行移動により、円 $C$ 上の点 $A(x_{1} \ , \ y_{1})$ は、円 $C’$ 上の点 $A'(x_{1}-a \ , \ y_{1}-b)$ に移る。
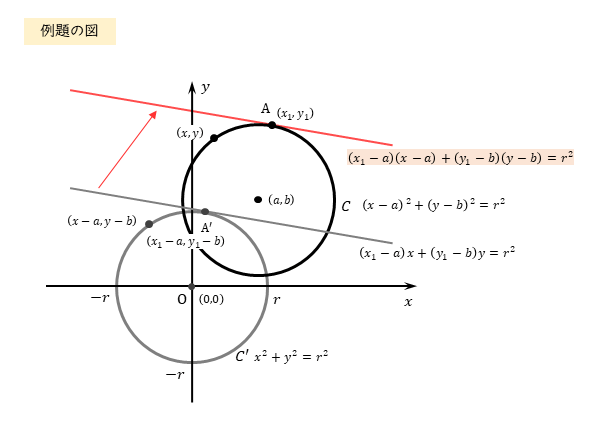
この点 $A'(x_{1}-a \ , \ y_{1}-b)$ における円 $C’$ の接線の方程式は
\begin{align} \quad \left(x_{1}-a \right)x+\left(y_{1}-b \right)y=r^{2} \end{align}となる。
ここで得られた接線は、原点を中心とする円の接線です。求めたい接線ではないことに注意しましょう。
与えられた円の接線を求めるには、元の位置に平行移動します。
例題の解答例 3⃣
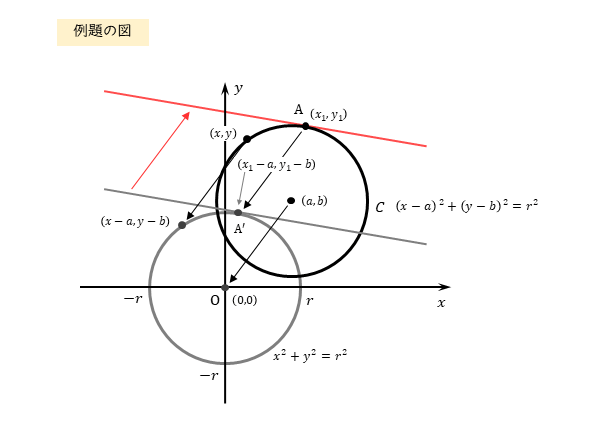
\begin{align} &\quad \vdots \\[ 7pt ] \quad &\left(x_{1}-a \right)x+\left(y_{1}-b \right)y=r^{2} \\[ 7pt ] &\quad \vdots \end{align}よって、この接線を $x$ 軸方向に $a$、$y$ 軸方向に $b$ だけ平行移動したものが、円 $C$ 上の点 $A$ における接線の方程式である。
したがって、その方程式は
\begin{align} \quad \left(x_{1}-a \right)\left(x-a \right)+\left(y_{1}-b \right)\left(y-b \right)=r^{2} \end{align}一般化された接線の公式を導出することができました。こちらは中心が原点の円でも問題なく利用できます。
また、図を1つにまとめると以下のようになります。イメージできるようにしておきましょう。
円の接線の方程式を求める流れをまとめると以下のようになります。
円の接線の方程式を求める手順
- 円を原点中心となるように平行移動させる
- 円の平行移動に伴って、接点も平行移動させる(接点の座標が変わる)
- 平行移動後の接点における接線の方程式を求める
- 3で求めた接線を平行移動させる
求めたい接線の方程式は、3ではなく4の方程式です。作図していないとよく勘違いするので注意しましょう。
図形の平行移動を2回行う(中心が原点になるように平行移動、円が元の位置になるように平行移動)ので注意しよう。
また、接線の方程式を求めるには、2次関数の平行移動で学習した事柄を利用しています。
一般に、関数を平行移動するとき、以下のことが成り立ちます。
一般化したグラフの平行移動
$y=f(x)$ のグラフを $x$ 軸方向に $p$ だけ、$y$ 軸方向に $q$ だけ平行移動する。
このとき
\begin{align} \quad y=f(x) \end{align}において、$x$ を $x-p$ に、$y$ を $y-q$ に置き換えて
\begin{align} \quad y-q=f \left(x-p \right) \end{align}よって
\begin{align} \quad y=f \left(x-p \right)+q \end{align}円の接線の方程式は公式化されています。入試などのように時間制限がある場合には積極的に利用しましょう。
円の接線の方程式(原点中心)
\begin{align} \quad x^{2}+y^{2}=r^{2} \ \cdots \ \text{①} \end{align}円①上の点 $(x_{1} \ , \ y_{1})$ における接線の方程式は
\begin{align} \quad x_{1} x+y_{1} y=r^{2} \end{align}円の接線の方程式(原点中心以外)
\begin{align} \quad \left(x-a \right)^{2}+\left(y-b \right)^{2}=r^{2} \ \cdots \ \text{②} \end{align}円②上の点 $(x_{1} \ , \ y_{1})$ における接線の方程式は
\begin{align} \quad \left(x_{1}-a \right)\left(x-a \right)+\left(y_{1}-b \right)\left(y-b \right)=r^{2} \end{align}次は、円上の点における接線を扱った問題を実際に解いてみましょう。