図形の性質|外心について

外心を扱った問題を解いてみよう
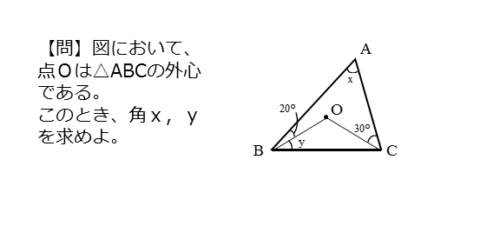
次の問題を考えてみましょう。
問の解答・解説
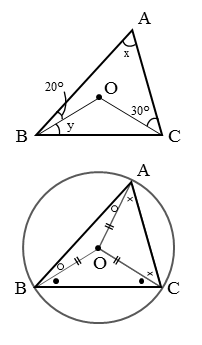
点Oは外心なので、△ABCの外接円を書き込みます。
外接円を描くことで、同一の弧に対する中心角や円周角を見つけやすくなります。
また、外心Oと頂点A,B,Cとを結んで3つの二等辺三角形をつくります。
二等辺三角形の底角は等しいので、大きさが等しい角に記号を書き込んでおきます。
与えられた図に書き込んでも構いませんが、積極的に自分で作図する習慣を付けておきましょう。
角に記号を入れたことでよく分かりますが、角xは∠OABと∠OACの和に等しい角です。△OABと△OACが二等辺三角形であることを利用します。
問の解答例 1⃣
$\triangle OAB$ において、$OA=OB$ であるので
\begin{align*} \quad \angle {OAB} = \angle {OBA} = 20^{\circ} \end{align*}同様に $\triangle OAC$ において、$OA=OC$ であるので
\begin{align*} \quad \angle {OAC} = \angle {OCA} = 30^{\circ} \end{align*}よって
\begin{align*} \quad x &= \angle BAC \\[ 7pt ] &= \angle {OAB}+\angle {OAC} \\[ 7pt ] &= 20^{\circ}+30^{\circ} \\[ 7pt ] &= 50^{\circ} \end{align*}次に角yを求めます。角yは、二等辺三角形である△OBCの底角です。△OBCの底角を求めるには、∠BOCを求めておく必要があります。
ここで、弧BCに対する円周角と中心角に注目すると、角xを利用できることに気付きます。同一の弧に対する中心角と円周角の関係を利用します。
問の解答例 2⃣
弧 $BC$ に対する中心角と円周角の関係より
\begin{align*} \quad \angle {BOC} = 2 \angle {BAC} = 100^{\circ} \end{align*}$\triangle OBC$ において、$OB=OC$ であるので
\begin{align*} \quad \angle {OBC} = \angle {OCB}=y \end{align*}三角形の内角の和より
\begin{align*} \quad \angle BOC+\angle OBC+\angle OCB = 180^{\circ} \end{align*}よって
\begin{align*} \quad 100^{\circ}+y+y = 180^{\circ} \end{align*}$y$ について解くと
\begin{align*} \quad y &=\frac{1}{2}\left(180^{\circ}-100^{\circ} \right) \\[ 7pt ] &=40^{\circ} \end{align*}角を求める問題では、三角形の内角の和をよく利用するので忘れないようにしましょう。
問のポイントと解答例をまとめると以下のようになります。
解答例では角yを△OBCの内角と考えましたが、△ABCの内角の一部と考えても求めることができます。この場合、△ABCにおいて内角の和を利用します。
問の別解例
$\triangle ABC$ において三角形の内角の和より
\begin{align*} \quad \angle {BAC} + \angle {ABC} + \angle {ACB} = 180^{\circ} \quad \cdots \text{①} \end{align*}ここで
\begin{align*} &\quad \angle {BAC} = \angle {BAO} + \angle {CAO} \\[ 7pt ] &\quad \angle {ABC} = \angle {ABO} + \angle {CBO} \\[ 7pt ] &\quad \angle {ACB} = \angle {ACO} + \angle {BCO} \end{align*}また、二等辺三角形の底角より
\begin{align*} &\quad \angle {BAO} = \angle {ABO} \\[ 7pt ] &\quad \angle {CBO} = \angle {BCO} \\[ 7pt ] &\quad \angle {CAO} = \angle {ACO} \end{align*}が成り立つので、これより①は
\begin{align*} \quad 2y + 100^{\circ} = 180^{\circ} \end{align*}よって
\begin{align*} \quad y= 40^{\circ} \end{align*}本問のように、複数の図形が混在する場合、どの図形に注目しているかによってアプローチの仕方が変わってきます。落ち着いてアプローチの仕方を考えましょう。
また、アプローチを吟味するときに困らないように、大きさや長さの等しい角や辺に記号を書き込むなどの最低限の作業を済ませておきましょう。
Recommended books
オススメその1
予習の際に理解が進めば授業のスピードについていくことができ、復習や課題をこなす時間も少なくて済みます。予習や復習の補助教材に向いている教材が『とってもやさしい数学』シリーズです。
とってもやさしい数学1・Aでは2冊とも中学で学習した内容にも触れており、中学内容と高校内容とのつながりを把握しやすい教材です。
一学期のうちは不安を抱えながら学習を進めていく人も多いかと思います。スタートで躓かないためにも易しく取り組みやすい教材を使うのも一つのやり方です。無理をして内容の難しい教材を使うよりもはるかに良いでしょう。
基礎的な内容を扱っているので、数学が苦手な人でも取り組みやすくなっています。興味のある人はぜひ一読してみて下さい。
『高校とってもやさしい数学1・A 改訂版 その1』は「数と式」「2次関数」の単元を扱っています。
『高校とってもやさしい数学1・A 改訂版 その2』は「場合の数」「確率」「整数の性質」「図形の性質」「三角比」の単元を扱っています。
オススメその2
『高校の数学I・Aが1冊でしっかりわかる本』は、これ1冊で数学1・Aの全範囲を復習できます。内容のレベルは「とってもやさしい」シリーズとそれほど変わらず、教科書レベルです。
本書と「とってもやさしい」シリーズのページ数を比較してみました。「とってもやさしい」シリーズは、1冊ごとのページ数が少ないのですが、分冊なのが難点です。
- 高校とってもやさしい数学1・A 改訂版 その1:175ページ
- 高校とってもやさしい数学1・A 改訂版 その2:189ページ
- 高校の数学I・Aが1冊でしっかりわかる本:192ページ
ページ数を比べると分かるように、本書の方が1冊でも遥かにページ数が少ないので、短時間でこなすことができます。
紹介した教材を使うとした場合、高校1年生であれば「とってもやさしい」シリーズで復習し、高校2,3年生であれば『高校の数学I・Aが1冊でしっかりわかる本』と「とってもやさしい」シリーズを組み合わせて復習すると良いでしょう。
こんな人に向いています
- 定期試験や大学受験のための基礎を固めて、成績を上げたい高校生へ。
- 医療看護系入試、高卒認定試験などの対策で、短期間で数学1・Aを理解したい方へ。
- 学び直しや頭の体操をしたい大人の方へ。
さいごに、もう一度、頭の中を整理しよう
- 外心は三角形の外接円の中心。
- 外心は三角形の3辺の垂直二等分線の交点。
- 三角形の内角を求めるとき、外接円にできた円周角と中心角の関係を利用しよう。
- 外心を頂点にもつ三角形は、二等辺三角形(または正三角形)になる。