数と式｜一次不等式を扱った応用問題を解いてみよう その３（道のり・速さ・時間）
今回は「一次不等式を扱った応用問題を解いてみよう」のその３です。ここでは、道のり・速さ・時間を題材にして、問題文の読み方や線分図の描き方などを紹介します。
道のり・速さ・時間を題材にした問題は、中学数学はもちろんですが、高校数学でも扱われます。ですから、確実に解けるようにしておきたい問題です。
この記事では不等式を扱いますが、立式までの大まかな流れは方程式とほとんど変わりません。中学数学の方程式の文章問題が苦手な人にも役立つ内容です。ぜひ一読してみて下さい。
道のり・速さ・時間を題材にした一次不等式の問題
さっそく問題です。
問
家から駅までの距離は $1.5 \ \mathrm{km}$ である。最初毎分 $60 \ \mathrm{m}$ で歩き、途中から毎分 $180 \ \mathrm{m}$ で走る。家を出発してから $12$ 分以内で駅に着くためには、最初に歩く距離を何 $\mathrm{m}$ 以内にすればよいか。
文章中から情報を読み取ろう
文章問題では、立式に必要な情報が必ず提示されています。数学の専門用語についての知識が必要なのは、大前提です。その大前提を踏まえて、情報を正しく読み取るためには、文章の読解力が必要です。
読解力がないと、何の話をしているのか分からなかったり、誤読したりするでしょう。このようなことが起きるのは、国語の学力が足りないことが原因かもしれません。
読解力を向上させるには、国語、特に現代文の学習に取り組んだ方が良いでしょう。数学だけに限らず、どの科目でも起きうることなので、現代文の学習にはしっかり取り組んだ方が吉です。
苦手な科目があるのは、その科目だけでなく、他の科目も影響しているかもしれない。
文章の読み方にはコツがあって、これが読解力につながります。数学の場合で言えば、立式することを意識して読むことです。そのためには、たとえば、以下の事柄に注目することが大切です。
問題を読むときに意識したいこと
- 求める数量は何か。
- どんな数量が与えられているか。
- 立式するのは、方程式（等式）なのか不等式なのか。
- 題材に関係する公式や定理はなかったか。
これらを意識しながら文章を読んでいけば、自ずとポイントになる数量や文言が目に入ってきます。
ただ眺めるように読めば良いというわけではない。どの科目、どの問題でも、目的を意識して読むことが大切。
道のり・速さ・時間を扱った文章問題の読み方
問
家から駅までの距離は $1.5 \ \mathrm{km}$ である。最初毎分 $60 \ \mathrm{m}$ で歩き、途中から毎分 $180 \ \mathrm{m}$ で走る。家を出発してから $12$ 分以内で駅に着くためには、最初に歩く距離を何 $\mathrm{m}$ 以内にすればよいか。
１つ１つの文章が短いので、それほど混乱することはないでしょうが、注目する箇所を確認しましょう。
与えられた数量を整理しよう
文章問題に限りませんが、問題では色々な数量が情報として与えられます。ここでは、道のり・速さ・時間を題材にしているので、これらに関する数量が与えられているはずです。
文章を読みながら、与えられた数量を丸や四角で囲みましょう。下線を引くことが多いかもしれませんが、下線よりも目立つのでより効果的です。
また、情報を整理していくとき、求める数量と単位を絶対に確認しましょう。
求める数量は、文章の終わりの方を読めば分かることがほとんどです。問題文では、「最初に歩く距離を何ｍ以内にすればよいか」とあるので、歩く距離をｘとおけば良いことが分かります。
また、単位は、速さを参考にして統一します。速さの単位を変換するより、道のりや時間の単位を変換する方が楽だからです。
速さの単位は、毎分６０ｍや毎分１８０ｍです。これを参考にすると、道のりの単位をメートル、時間の単位を分に統一します。
与えられた数量を整理します。文章問題が苦手な人については、少し手間が掛かりますが、たとえば、表にまとめると良いでしょう。
道のり・速さ・時間の情報を整理 1⃣
数量が不明のものは、この時点では無理をして埋める必要はありません。ただし、速さの合計は足し算では得られないので、合計の欄に斜線を引いておきましょう。
求めるものは歩く距離なので、歩く距離の欄にｘｍを追記します。何をｘとおくかが決まれば、残りの数量も決まります。
道のり・速さ・時間の情報を整理 2⃣
表にまとめてしまえば、このまま立式することができます。
ここでは表を利用しましたが、線分図を利用して立式するのが一般的です。物理基礎や物理では、線分図を描くので、表よりも線分図に慣れておいた方が良いでしょう。
次は作図の手順を解説します。
道のり・速さ・時間を扱った文章問題の作図
問題を読みながら、与えられた数量を丸や四角で囲んだら、それらをもとに線分図を描きます。
ほとんどの文章問題では、読んだ順に数量を追記していけば、立式に必要な図が自然と完成します。
１番目の文章の作図
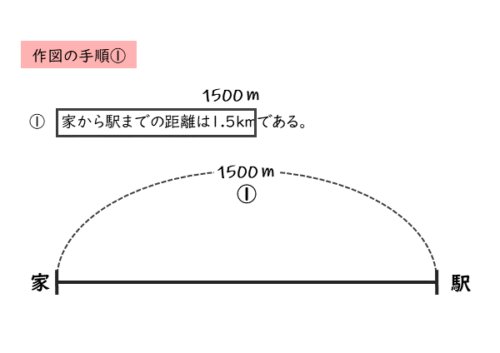
１番目の文章
家から駅までの距離は $1.5 \ \mathrm{km}$ である。
１番目の文章から、家から駅までの距離が分かります。適当な長さの線分を引きます。
線分全体の長さが家から駅までの距離に相当します。線分全体を示すように １.５ｋｍ＝１５００ｍを追記します。
追記する数量が、どの範囲に対応するのかをはっきりさせましょう。また、数字だけでなく、単位も添えて追記しましょう。
単位を添えるのは、異なる単位の数量があれば誤用せずに済むからです。作図は内容の理解を助けるためのものなので、曖昧だと混乱の元になります。
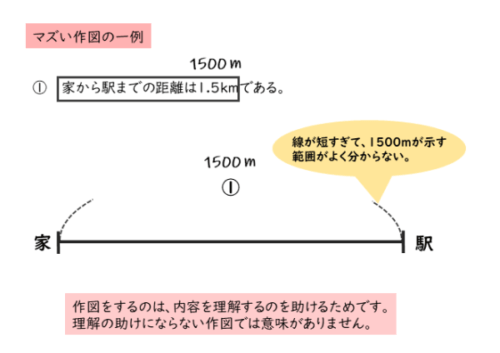
マズい作図の一例を挙げておきます。
マズい作図の場合、数量が書いてあっても、その数量が指し示す対象が曖昧です。
この問題では、区間が複数あるので、特に注意しなければなりません。
作図は、内容を理解するときの助けになるもの。理解の助けにならない作図や、ミスを誘発するような作図は避けよう。
２番目の文章の作図
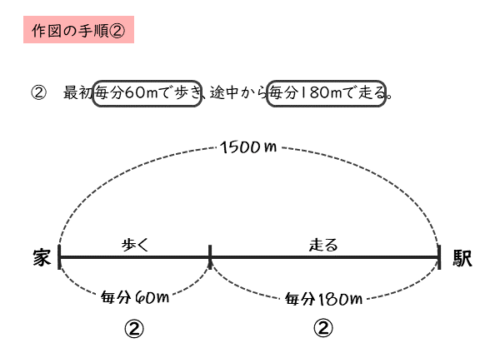
２番目の文章
最初毎分 $60 \ \mathrm{m}$ で歩き、途中から毎分 $180 \ \mathrm{m}$ で走る。
２番目の文章から、家と駅の間には歩く区間と走る区間があることが分かります。
適当に線分を分割して、歩く区間と走る区間における速さをそれぞれ追記します。
３番目の文章前半の作図
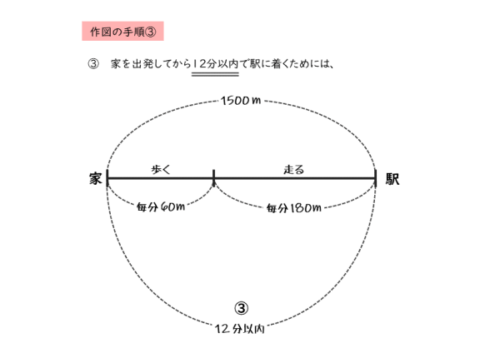
３番目の文章前半
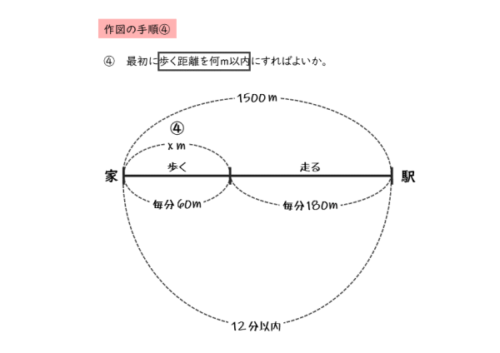
家を出発してから $12$ 分以内で駅に着くためには、
３番目の文章前半から、家を出発してから駅に着くまでの時間が分かります。
線分全体を示すように、「１２分以内」の文言を追記します。
３番目の文章後半の作図
３番目の文章後半
最初に歩く距離を何 $\mathrm{m}$ 以内にすればよいか。
３番目の文章後半から、歩く距離が求める数量だと分かります。
歩く距離をｘｍとして、これを歩く区間に追記します。
残りの作図
このままでは、走る区間の距離、歩く時間、走る時間などの情報がありません。
これらは問題では与えられていない情報であり、自分で入手しなければならない情報です。ここがこの問題のポイントです。
歩く距離ｘｍを用いて追記していきます。
残りの情報を入手する
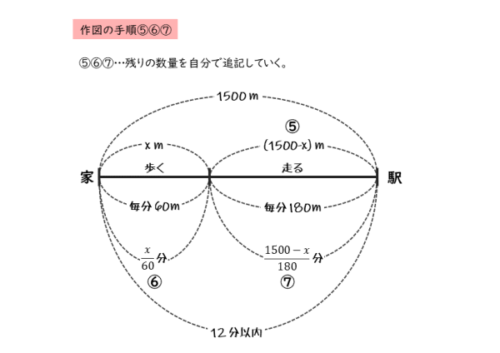
最初に歩いた距離を $xm$ とすると、走った距離は $(1500-x) \ \mathrm{m}$
毎分 $60 \ \mathrm{m}$ で $x \ \mathrm{m}$ 歩くので、要する時間は $\frac{x}{60}$ 分
毎分 $180 \ \mathrm{m}$ で $(1500-x) \ \mathrm{m}$ 走るので、要する時間は $\frac{1500-x}{180}$ 分
残りの情報を追記すると以下のようになります。
線分図を見て分かるように、上から順に道のり、速さ、時間と並んでいます。
好き勝手に数値を追記していくのではなく、規則性を持たせて追記しましょう。
自分なりにルールを決めて、同じ形式で作図できるようにしておくと良いでしょう。
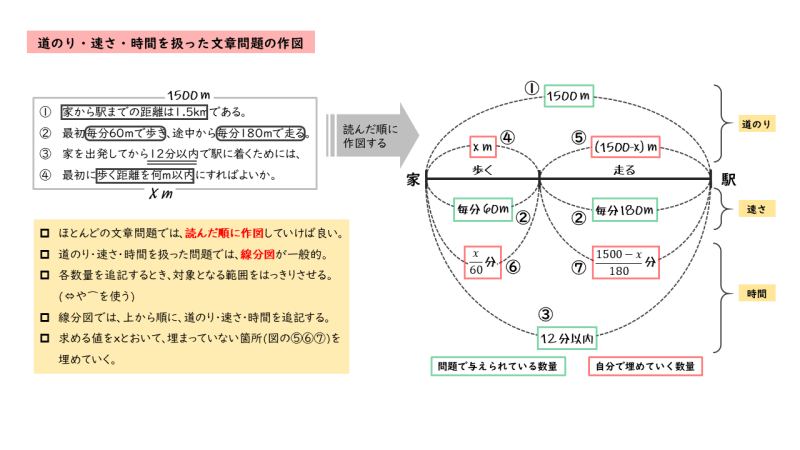
道のり・速さ・時間を扱った文章問題について、作図のポイントや手順をまとめると以下のようになります。
線分図を描くとき、与えられた情報と自分で導く情報との区別、言い換えると、情報の整理も一緒に進めています。
難しく感じる人がいるかもしれませんが、慣れるまでは、決まった手順を繰り返すことです。飲み込みの良い人が行っている習慣です。
慣れないうちに好き勝手にすると、定着するのに時間が掛かります。自分なりに作図の手順を決めて、繰り返し訓練しましょう。
表や線分図から立式しよう
道のり・速さ・時間を扱った文章問題では、道のりと時間のどちらかについて立式します。速さで立式することはまずありません。
問題では、家から出発して駅に着くために「１２分以内で」という条件があるので、不等式で立式します。もし、「１２分で」となっていれば、等式で立式します。
歩く区間と走る区間の道のりや速さが異なるので、各区間ごとに要する時間を求めます。これらの時間の和が１２分以内であれば良いわけです。
立式すると以下のようになります。
立式する
歩いた時間と走った時間の合計が $12$ 分以内であれば良いので
\begin{align*} &\quad \text{(歩いた時間)} + \text{(走った時間)} \ \leqq 12 \\[ 7pt ] &\text{よって} \\[ 7pt ] &\quad \frac{x}{60} + \frac{1500-x}{180} \leqq 12 \end{align*}「以内」は、以上や以下と同じように、等号のときを含む言葉です。立式できれば、あとは一次不等式の計算問題です。
一次不等式を解こう
不等式は分数を含むので、両辺に１８０を掛けて分母を払います。移項は分母を払ってからにします。
分母を払ってから移項
１２と１８０の掛け算をしても良いですが、筆算を避けるために、右辺の掛け算を左辺の整理よりも後回しにしました。その結果、両辺を２で割ることができ、左辺を暗算で整理できました。
記述例は以下のようになります。
問題の記述例
ここで扱った問題は、それほど複雑ではなかったので、立式するのは簡単だったと思います。そうは言っても、基本的な手順は、複雑そうな問題であっても変わりません。
異なるとすれば、表現が難しかったり、公式や定理の予備知識が必要だったりすることです。色々なものを題材にした文章問題があるので、コツを掴めたらチャレンジしてみましょう。
Recommended books
大学進学を考えたとき、記述を重視した学習を日常的に行った方が良いでしょう。試験の難易度は、マーク形式よりも記述形式の方が高いからです。
また、記述では思考力や表現力などが必要で、それらを身に付けるのは一朝一夕には難しいことも理由の１つです。
記述の訓練は、基本的に教科書や参考書の例題を真似することから始まりますが、記号の使い分けや独特の表現などがあり、手探りで進めていくのは大変です。
そこでお勧めしたいのが以下の２冊です。記述の訓練に特化したテキストになります。
オススメその１
１冊目は『基礎からのジャンプアップノート 数学 記述式答案 書き方ドリル』で、数学に苦手意識のある人におすすめです。
数学Ⅰ＋Ａ＋Ⅱ＋Ｂの記述力の基礎力を固めるなら、まずはこのドリルから！！
問題編６４ページ、別冊解答編３２ページ
- 証明問題、場合分けの答案の書き方のコツがわかる
- 「なぞって理解する」書き込みノートだから、わかりやすい答案の書き方が覚えやすい
- 「例（手本）」→「Check！」→「練習問題」 まねる＆繰り返すの流れで、記述力UP！
- 別冊「解答編」では、練習問題をくわしく解答
『基礎からのジャンプアップノート』は数学以外の科目にもあります。基礎レベルの内容を扱っており、ページ数も多くありません。日常学習での予習や復習に使い勝手が良いでしょう。
オススメその２
２冊目は『総合的研究 記述式答案の書き方ーー数学I・A・II・B』です。数学に苦手意識がなく、将来的に得意科目にしたい人向けです。
『総合的研究』シリーズは、チャート式やフォーカスゴールドなどと並んで有名な参考書で、数学以外の科目もあります。また、電子書籍でも出版されているので、持ち運びに苦労しないのもポイントが高いです。
この本のテーマは《伝える》ことです。私たちは、この本で、数学的に正当な思考・数学的な事実を、どうすれば文章にして他者に伝えられるか、懸命に説明しています。
ちょっとした言葉づかい、論理的な説明の順序、条件と命題の違いの意識、いろいろな文字の立場の理解・・・・・・きっと、読者の皆さんの考えを読み手に《伝える》ために、すぐ役立つはずです。
（中略）数学の答案作りとは、自分と読み手のあいだに小さいながらも数学の世界を築く作業です（抽象的な言い方ですが、数学的に正しい主張とは、常に完結した、バランスの取れた小宇宙です）。
自分の知性と読み手の知性、双方を信頼し、両者の思考をつなぎ、そこに確固たる数学的結論を創造する。この営みは、多くの中高生が考えているより、ずっとやりがいのあるものです。
この本を手に取られたあなたが、この本を通じて答案作成の方法を知り、そのたのしみに触れていただけることを祈ります。
それでは、《伝える》レッスンをはじめましょう！（まえがきより）
著者が異なりますが、こちらも『総合的研究』シリーズです。
さいごに、もう一度まとめ
- 求める数量を絶対に押さえよう。
- 単位を統一しよう。
- 与えられた数量を丸や四角で囲もう。
- 方程式と不等式のどちらで立式するかを考えよう。
- 線分図を描こう。