数学1,数学A
第1問〔2〕について
第1問〔2〕は「集合と論理」を扱った問題です。小問2つの構成です。
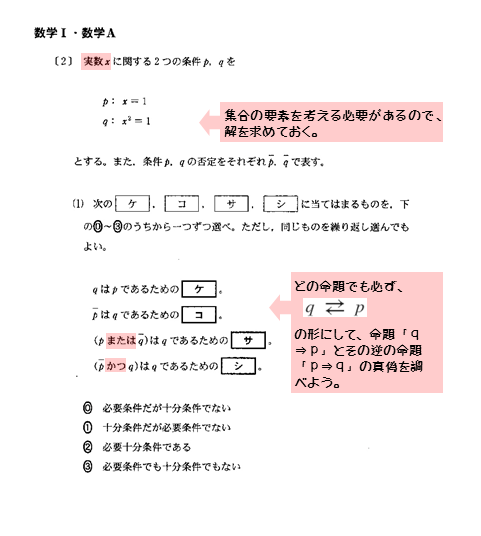 第1問〔2〕(1)
第1問〔2〕(1)
 第1問〔2〕(2)
第1問〔2〕(2)
(1)は「必要条件・十分条件」に関する問題です。
必要条件や十分条件を考えるとき、条件を満たす要素が属する集合の包含関係を調べます。そのためには、与えられた条件のままで必要条件や十分条件を考えても上手くいきません。
たとえば、条件qであれば、2次方程式をそのままにせず、解を求めて要素を把握する必要があります。
また、(1),(2)の両方に条件p,qの否定が出てくるので、条件p,qの否定をしっかり書き出しておきましょう。
解答欄ケ
解答欄ケの問題は、条件qが条件pに対してどんな立場の条件かを考える問題です。命題「q⇒p」と命題「q⇐p」の真偽を調べることで、どんな立場の条件なのかが分かります。
xは実数なので、実数全体が属する集合を全体集合Uと定義します。また、条件p,qに対応する集合をそれぞれP,Qとします。
このとき、集合P,Qに属する要素は以下のようになります。
解答欄ケの解答例 1⃣
\begin{align*}
&\text{条件 $p$ に対応する集合を $P$ とすると} \\[ 5pt ]
&\quad P=\left\{ 1 \right\} \\[ 7pt ]
&\text{条件 $q$ に対応する集合を $Q$ とすると} \\[ 5pt ]
&\quad x^{\scriptsize{2}}=1 \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad x= \pm 1 \\[ 7pt ]
&\text{よって} \\[ 5pt ]
&\quad Q=\left\{ -1 \ , \ 1 \right\}
\end{align*}
 第1問〔2〕(1)
第1問〔2〕(1)
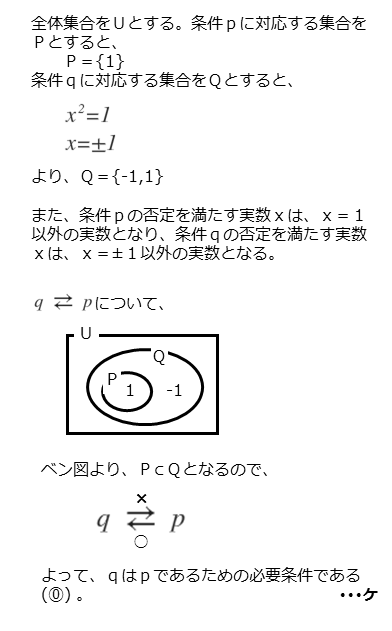
次に集合P,Qの包含関係を調べます。2つの集合の包含関係が分かれば、命題「q⇒p」と命題「q⇐p」の真偽を知ることができます。集合の包含関係を考えるには、一般にベン図を利用します。
ここでは、各集合の要素が少ないので、ベン図なしでも問題ないでしょう。
集合P,Qの包含関係から各命題の真偽を調べます。その結果から必要条件・十分条件を判断します。
解答欄ケの解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad P=\left\{ 1 \right\} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad Q=\left\{ -1 \ , \ 1 \right\} \\[ 7pt ]
&\text{$2$ つの集合 $P \ , \ Q$ の包含関係を調べると} \\[ 5pt ]
&\quad Q \supset P \\[ 7pt ]
&\text{であるので} \\[ 5pt ]
&\quad \text{$q$ ならば $p$ は偽} \\[ 7pt ]
&\quad \text{$p$ ならば $q$ は真} \\[ 7pt ]
&\text{よって、$q$ は $p$ であるための必要条件である。}
\end{align*}
命題「q⇒p」が偽で、命題「q⇐p」が真であるので、十分条件ではありませんが、必要条件であることが分かります。
集合の包含関係は命題の真偽に対応している。ベン図を上手に利用しよう。
 解答欄ケの解答例
解答欄ケの解答例解答欄コ
解答欄コの問題は、条件pの否定が条件qに対してどんな立場の条件かを考える問題です。命題「pの否定⇒q」と命題「pの否定⇐q」の真偽を調べることで、どんな立場の条件なのかが分かります。
条件p,qの否定と、その集合を求めます。
解答欄コの解答例 1⃣
\begin{align*}
&\text{条件 $p$ の否定 $\overline{p}$ は} \\[ 5pt ]
&\quad x \neq 1 \\[ 7pt ]
&\text{これに対応する集合 $\overline{P}$ の要素は} \\[ 5pt ]
&\quad P=\left\{x \ | \ x=1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\text{また、条件 $q$ の否定 $\overline{q}$ は} \\[ 5pt ]
&\quad x^{\scriptsize{2}} \neq 1 \\[ 7pt ]
&\text{これに対応する集合 $\overline{Q}$ の要素は} \\[ 5pt ]
&\quad Q=\left\{x \ | \ x=\pm 1 \ \text{以外のすべての実数} \right\}
\end{align*}
 第1問〔2〕(1)
第1問〔2〕(1)
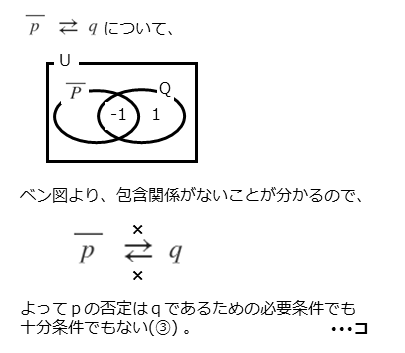
条件pの否定を満たす実数xは、集合Pの補集合に属する要素です。この集合Pの補集合と、集合Qとの包含関係を調べます。要素だけで分かりにくければ、ベン図も上手に利用しましょう。
解答欄コの解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&\quad \overline{P}=\left\{x \ | \ x=1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad \vdots \\[ 7pt ]
&\quad Q=\left\{-1 \ , \ 1 \right\} \\[ 7pt ]
&\text{集合 $\overline{P}$ と集合 $Q$ の包含関係は} \\[ 5pt ]
&\quad \overline{P} \not \subset Q \ , \ \overline{P} \not \supset Q \\[ 7pt ]
&\text{これより、$2$ つの集合に包含関係はないので} \\[ 5pt ]
&\quad \text{$\overline{p}$ ならば $q$ は偽} \\[ 7pt ]
&\quad \text{$q$ ならば $\overline{p}$ は偽}
\end{align*}
よって、$\overline{p}$ は $q$ であるための必要条件でも十分条件でもない。
集合Pの補集合と集合Qとは、部分的に重なる(共通部分をもつ)だけで、包含関係はありません。このことはベン図の方が分かりやすいでしょう。
 解答欄コの解答例
解答欄コの解答例 解答欄サ
解答欄サの問題は、(条件pまたは条件qの否定)が条件qに対してどんな立場の条件かを考える問題です。
命題「(pまたはqの否定)⇒q」と命題「(pまたはqの否定)⇐q」の真偽を調べることで、どんな立場の条件なのかが分かります。
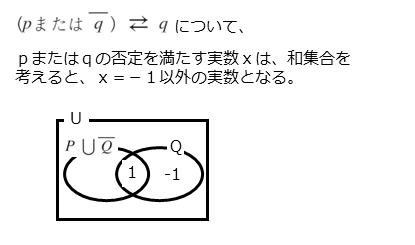
条件qの否定を満たす実数xは、集合Qの補集合に属する要素です。この集合Qの補集合と集合Pの和集合が、条件pまたは条件qの否定を満たすxを要素とする集合です。
このような和集合と集合Qの包含関係を調べます。要素だけで分かりにくければ、ベン図も上手に利用しましょう。
解答欄サの解答例
\begin{align*}
&\quad P=\left\{ 1 \right\} \\[ 7pt ]
&\quad \overline{P}=\left\{x \ | \ 1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad Q=\left\{ -1 \ , \ 1 \right\} \\[ 7pt ]
&\quad \overline{Q} =\left\{x \ | \ -1 \ , \ 1 \ \text{以外のすべての実数} \right\} \\[ 10pt ]
&\text{$p$ または $\overline{q}$ に対応する集合 $P$ または $\overline{Q}$ は} \\[ 5pt ]
&\quad P \cup \overline{Q}=\left\{x \ | \ -1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\text{これと集合 $Q$ の包含関係は} \\[ 5pt ]
&\quad \left(P \cup \overline{Q} \right) \not \subset Q \ , \ \left(P \cup \overline{Q} \right) \not \supset Q \\[ 7pt ]
&\text{$2$ つの集合に包含関係はないので} \\[ 5pt ]
&\quad \text{( $p$ または $\overline{q}$ )ならば $q$ は偽} \\[ 7pt ]
&\quad \text{$q$ ならば( $p$ または $\overline{q}$ )は偽}
\end{align*}
よって、( $p$ または $\overline{q}$ )は $q$ であるための必要条件でも十分条件でもない。
 第1問〔2〕(1)
第1問〔2〕(1)
集合Pと集合Qの補集合の和集合と、集合Qとは、部分的に重なる(共通部分をもつ)だけで、包含関係はありません。ベン図を上手に利用しましょう。
 解答欄サの解答例①
解答欄サの解答例①
 解答欄サの解答例②
解答欄サの解答例②
解答欄シ
解答欄シの問題は、条件pかつ条件qが条件qに対してどんな立場の条件かを考える問題です。
命題「(pの否定かつq)⇒q」と命題「(pの否定かつq)⇐q」の真偽を調べることで、どんな立場の条件かが分かります。
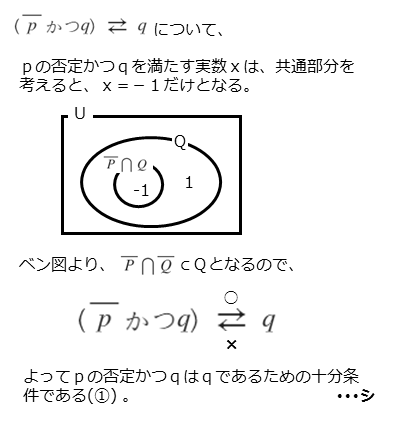
条件pの否定を満たす実数xは、集合Pの補集合に属する要素であり、すでに分かっています。この集合Pの補集合と集合Qの共通部分が、条件pの否定かつ条件qを満たすxを要素とする集合です。
このような共通部分と集合Qの包含関係を調べます。要素だけで分かりにくければ、ベン図も上手に利用しましょう。
解答欄シの解答例
\begin{align*}
&\quad P=\left\{ 1 \right\} \\[ 7pt ]
&\quad \overline{P}=\left\{x \ | \ 1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad Q=\left\{ -1 \ , \ 1 \right\} \\[ 7pt ]
&\quad \overline{Q} =\left\{x \ | \ -1 \ , \ 1 \ \text{以外のすべての実数} \right\} \\[ 10pt ]
&\text{$\overline{p}$ かつ $q$ に対応する集合 $\overline{P}$ かつ $Q$ は} \\[ 5pt ]
&\quad \overline{P} \cap Q=\left\{-1 \right\} \\[ 7pt ]
&\text{これと集合 $Q$ の包含関係は} \\[ 5pt ]
&\quad \left(\overline{P} \cap Q \right) \not \subset Q \ , \ \left(\overline{P} \cap Q \right) \not \supset Q \\[ 7pt ]
&\text{$2$ つの集合に包含関係はないので} \\[ 5pt ]
&\quad \text{( $\overline{p}$ かつ $q$ )ならば $q$ は偽} \\[ 7pt ]
&\quad \text{$q$ ならば( $\overline{p}$ かつ $q$ )は偽}
\end{align*}
よって、( $\overline{p}$ かつ $q$ )は $q$ であるための必要条件でも十分条件でもない。
 第1問〔2〕(1)
第1問〔2〕(1)
集合Pの補集合と集合Qの共通部分と、集合Qとは、部分的に重なる(共通部分をもつ)だけで、包含関係はありません。
 解答欄シの解答例
解答欄シの解答例どの問題も条件から集合とその要素を求める必要があります。それだけなく、集合どうしの包含関係も調べなくてはなりません。ただ、ベン図を利用すれば、それほど難しくない問題です。
第1問〔2〕(1)のポイントと解答例をまとめると以下のようになります。
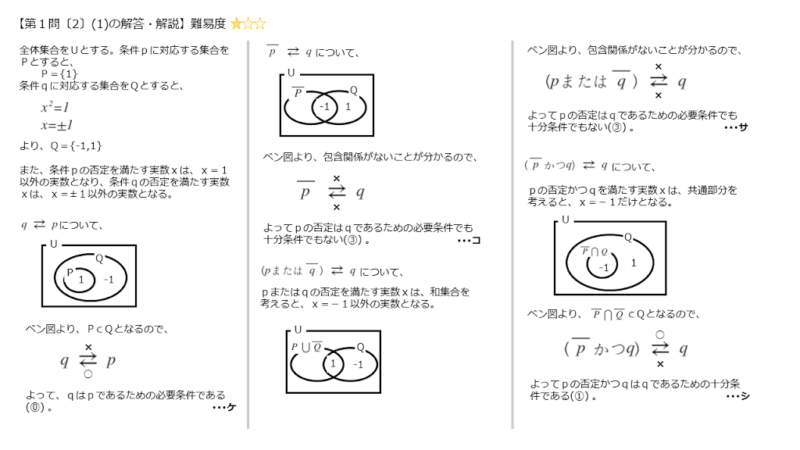 第1問〔2〕(1)のポイントと解答例
第1問〔2〕(1)のポイントと解答例 解答欄ス
第1問〔2〕(2)は「命題の真偽」に関する問題です。
条件rが新たに追加されましたが、(1)と同じように集合の包含関係から命題の真偽を考えます。
問題をよく見ると、条件rは不等式で与えられています。
この場合、ベン図ではなく数直線の方が分かりやすいかもしれません。
 第1問〔2〕(2)
第1問〔2〕(2)
まず命題A「(pかつq)⇒r」の真偽を調べます。ここで、条件rに対応する集合をRとします。
解答欄スの解答例 1⃣
\begin{align*}
&\quad P=\left\{ 1 \right\} \\[ 7pt ]
&\quad \overline{P}=\left\{x \ | \ 1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad Q=\left\{ -1 \ , \ 1 \right\} \\[ 7pt ]
&\quad \overline{Q} =\left\{x \ | \ -1 \ , \ 1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad R =\left\{x \ | x \gt 0 \ \text{を満たす実数} \right\} \\[ 10pt ]
&\text{$p$ かつ $q$ に対応する集合 $P$ かつ $Q$ は} \\[ 7pt ]
&\quad P \cap Q=\left\{ 1 \right\} \\[ 7pt ]
&\text{これと集合 $R$ の包含関係は} \\[ 5pt ]
&\quad \left(P \cap Q \right) \subset Q \\[ 7pt ]
&\text{より} \\[ 5pt ]
&\quad \text{( $p$ かつ $q$ )ならば $q$ は真} \\[ 7pt ]
&\text{よって、命題 $A$ は真}
\end{align*}
 第1問〔2〕(2)
第1問〔2〕(2)
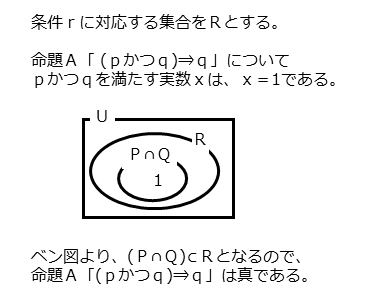 命題Aの真偽
命題Aの真偽次に命題B「q⇒r」の真偽を調べます。
解答欄スの解答例 2⃣
\begin{align*}
&\quad P=\left\{ 1 \right\} \\[ 7pt ]
&\quad \overline{P}=\left\{x \ | \ 1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad Q=\left\{ -1 \ , \ 1 \right\} \\[ 7pt ]
&\quad \overline{Q} =\left\{x \ | \ -1 \ , \ 1 \ \text{以外のすべての実数} \right\} \\[ 7pt ]
&\quad R =\left\{x \ | x \gt 0 \ \text{を満たす実数} \right\} \\[ 10pt ]
&\text{集合 $Q$ と集合 $R$ の包含関係は} \\[ 5pt ]
&\quad Q \not \supset R \ , \ Q \not \subset R \\[ 7pt ]
&\text{$2$ つの集合に包含関係はないので} \\[ 5pt ]
&\quad \text{$q$ ならば $r$ は偽} \\[ 7pt ]
&\text{よって、命題 $B$ は偽}
\end{align*}
 第1問〔2〕(2)
第1問〔2〕(2)
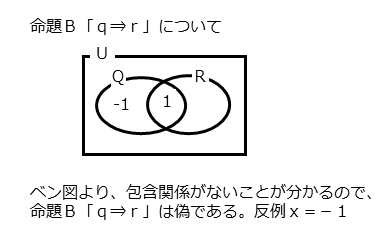 命題Bの真偽
命題Bの真偽最後に命題C「qの否定⇒pの否定」の真偽を調べます。
ところで、命題Cは命題「p⇒q」の対偶です。命題「p⇒q」の真偽は(1)で分かっているので、その結果を利用します。
命題「p⇒q」は真であるので、その対偶である命題Cも真です。
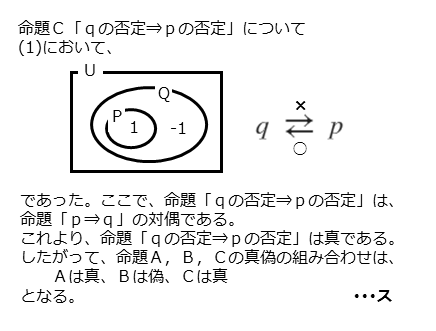 命題Cの真偽
命題Cの真偽今回は例年のように対偶を求める問題がありませんでしたが、最後の問題に出てきました。もちろん対偶を利用しなくても、直接求めることはできます。
第1問〔2〕(2)のポイントと解答例をまとめると以下のようになります。
 第1問〔2〕(2)のポイントと解答例
第1問〔2〕(2)のポイントと解答例 次は第1問〔3〕を解いてみましょう。























