数学１・Ａ｜2017センター試験・第１問を解いてみよう

07/18/2021数学１,数学Ａ

第１問〔３〕について

第１問〔３〕は「２次関数」を扱った問題です。

2016年のセンター試験では「２次関数」からの出題がありませんでしたが、2017年では第１問の小問として復活しました。全体の構成は以下のようになっています。

「２次関数」からの出題内容

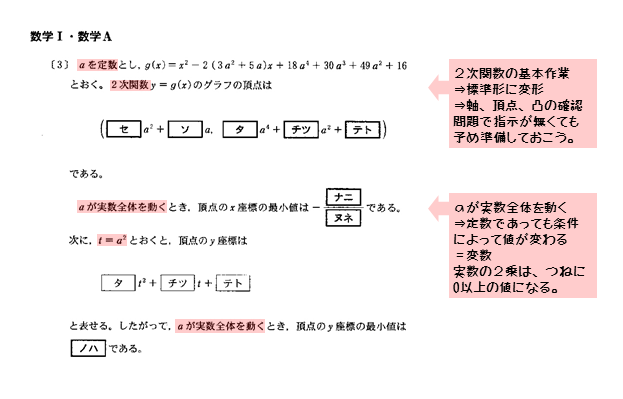
頂点の座標を求める問題
頂点のｘ座標の最小値を求める問題
頂点のｙ座標の最小値を求める問題

どれも頻出の問題ですが、難易度を上げているのが与えられた式ｇ(ｘ)です。

与式ｇ(ｘ)にはｘ以外にも文字ａがあり、その累乗を含む項が多いのが特徴です。変形でミスを誘うような式になっています。

解答欄セソ、タチツテト

最初の小問は、頂点の座標を求める問題です。頂点の座標を求めるには、与式を２次関数の標準形に変形します。

標準形への変形は、問題で特に指示されていない場合でも行いましょう。

与式には文字ａが含まれますが、ａは定数なので数と同じ扱いをします。

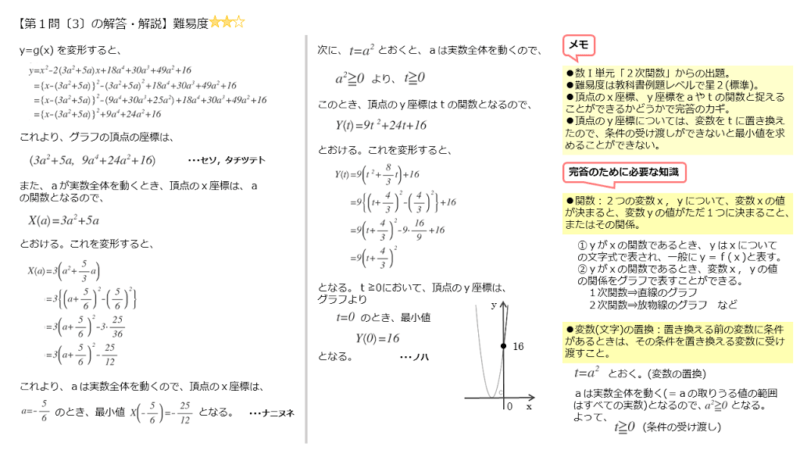
解答欄セソ、タチツテトの解答例

\begin{align*} &\quad y=x^{\scriptsize{2}}-2\left(3a^{\scriptsize{2}}+5a \right)x+18a^{\scriptsize{4}}+30a^{\scriptsize{3}}+49a^{\scriptsize{2}}+16 \\[ 7pt ] &\text{$y=g(x)$ を変形すると} \end{align*} \begin{align*} \quad y &=x^{\scriptsize{2}}-2\left(3a^{\scriptsize{2}}+5a \right)x+18a^{\scriptsize{4}}+30a^{\scriptsize{3}}+49a^{\scriptsize{2}}+16 \\[ 7pt ] &=\left\{ x-\left(3a^{\scriptsize{2}}+5a \right) \right\}^{\scriptsize{2}}-\left(3a^{\scriptsize{2}}+5a \right)^{\scriptsize{2}}+18a^{\scriptsize{4}}+30a^{\scriptsize{3}}+49a^{\scriptsize{2}}+16 \\[ 7pt ] &=\left\{ x-\left(3a^{\scriptsize{2}}+5a \right) \right\}+9a^{\scriptsize{4}}+24a^{\scriptsize{2}}+16 \end{align*} \begin{align*} &\text{よって、頂点の座標は} \\[ 5pt ] &\left(3a^{\scriptsize{2}}+5a \ , \ 9a^{\scriptsize{4}}+24a^{\scriptsize{2}}+16 \right) \end{align*}

右辺が非常に長く、複雑に見えますが、慌てず確実に平方完成します。

このような項の多い式の変形では、符号ミスが多くなります。丁寧に変形しましょう。難しく感じるかもしれませんが、数学２・Ｂのことを考えてサッとこなせるレベルにしておきましょう。

２次関数の平方完成は「１次の項の係数の半分、半分の２乗を引く」の順番で。

解答欄ナニヌネ

次の小問は、頂点のｘ座標の最小値を求める問題です。

頂点の座標を求めた結果、頂点のｘ座標がａで表されることが分かります。ａは定数でしたが、この問題で「ａは実数全体を動く」という条件が追加されました。

この条件からａは定数ではありますが、すべての実数が対象です。つまり、変数のような扱いになったということです。

このようなａによって頂点のｘ座標が表されます。ａの値が決まると、頂点のｘ座標はただ１つに決まるので、頂点のｘ座標はａの関数であると言えます。しかも、頂点のｘ座標はａの２次式で表されるので、２次関数です。

関数だからと言って、いつもｘ，ｙの文字を使っているとは限らない。関数の定義をしっかり理解しよう。

頂点のｘ座標はａの２次関数になっているので、平方完成して標準形に変形します。

解答欄ナニヌネの解答例

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left(3a^{\scriptsize{2}}+5a \ , \ 9a^{\scriptsize{4}}+24a^{\scriptsize{2}}+16 \right) \\[ 7pt ] &\text{頂点の $x$ 座標について} \\[ 5pt ] &\quad X(a)=3a^{\scriptsize{2}}+5a \\[ 7pt ] &\text{とおくと、頂点の $x$ 座標は $a$ の $2$ 次関数である。} \\[ 5pt ] &\text{このとき} \end{align*} \begin{align*} \quad X(a) &=3\left(a+\frac{5}{6} \right)^{\scriptsize{2}}-3 \cdot \left(\frac{5}{6} \right)^{\scriptsize{2}} \\[ 7pt ] &=3\left(a+\frac{5}{6} \right)^{\scriptsize{2}}-\frac{25}{12} \end{align*} \begin{align*} &\text{$a$ は実数全体を動くので、$X(a)$ の最小値は} \\[ 5pt ] &\quad a=-\frac{5}{6} \ \text{のとき、最小値} \ -\frac{25}{12} \end{align*}

標準形に変形した後、軸・頂点・凸の情報を確認して、グラフを描きます。標準形の式から、グラフが下に凸の放物線だと分かります。

また、定義域はａの取り得る範囲なので、すべての実数です。定義域がすべての実数であるとき、下に凸のグラフであれば、頂点のｙ座標が最小値になります。

解答欄ノハ

次の小問は、頂点のｙ座標の最小値を求める問題です。

文章中に「ｔ＝ａ²とおくと」という表現があります。これは、次数を下げるときに使われる手法です。頂点のｙ座標はａの４次式なので、文字を置き換えると次数が下がってｔの２次式になります。

次数を落とすことで、２次関数に帰着させて解く方法。指数関数などではよく使う。

このような文字の置き換えをするとき、注意すべきことがあります。

それは「置換前の文字ａ²の条件を、置換後の文字ｔに受け渡す」ということです。これを忘れる人が多いので気を付けましょう。

解答欄ノハの解答例

\begin{align*} &\quad \vdots \\[ 7pt ] &\quad \left(3a^{\scriptsize{2}}+5a \ , \ 9a^{\scriptsize{4}}+24a^{\scriptsize{2}}+16 \right) \\[ 7pt ] &\quad \vdots \\[ 7pt ] &\text{頂点の $y$ 座標について} \\[ 5pt ] &\quad a^{\scriptsize{2}}=t \\[ 7pt ] &\text{とおくと、$a$ はすべての実数なので} \\[ 5pt ] &\quad a^{\scriptsize{2}} \geqq 0 \ \text{すなわち} \ t \geqq 0 \\[ 7pt ] &\text{このとき} \end{align*} \begin{align*} \quad Y(t) &=9t^{\scriptsize{2}}+24t^{\scriptsize{2}}+16 \\[ 7pt ] &=\left(3t+4 \right)^{\scriptsize{2}} \\[ 7pt ] &=\left\{3\left(t+\frac{4}{3} \right\}^{\scriptsize{2}} \\[ 7pt ] &=9\left(t+\frac{4}{3} \right)^{\scriptsize{2}} \end{align*} \begin{align*} &\text{$t \geqq 0$ より、$Y(t)$ の最小値は} \\[ 5pt ] &\quad t=0 \ \text{のとき、最小値} \ 16 \end{align*}

ａはすべての実数であるので、ａ²は０以上の値になります。これより、ｔも０以上の値になります。これが定義域になります。

ｔに置き換えた後の式を標準形に変形します。標準形の式から、下に凸の放物線になります。ここでは、定義域があるので、頂点のｙ座標が最小値になるとは限りません。

もし、条件の受け渡しをしていなければ、ａがすべての実数という条件から、頂点のｙ座標が最小値になると考えるでしょう。これでは求めた解が解答欄に合わないので、非常に焦っただろうと思います。良く考えられた問題だと思います。

定義域ｔ≧０におけるグラフを書けば、ｔ＝０のときの頂点のｙ座標が最小値になることが分かります。

第１問〔３〕のポイントと解答例をまとめると以下のようになります。

第１問〔３〕のように、頂点の座標を関数と見立て、その関数の最大値や最小値を求める問題は過去に何度も出題されています。

第１問は完答を見込める大問だと思います。そうでなくても高校数学の最初の方の単元で、基本的な内容の多いところからの出題です。他の単元に与える影響は少なくないので、この単元をしっかりマスターしておく必要があるのではないかと思います。

教科書で確認しておきたい知識

乗法公式を利用した展開・因数分解
平方根の性質
実数などの数の分類
命題や集合などの用語の定義
共通部分と和集合
命題の真偽と集合の包含関係との関わり
２次関数の標準形への式変形
関数の最小値（定義域の有無）

Recommended books

さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。

難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。

傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。