数学１・Ａ｜2017センター試験・第３問を解いてみよう

11/13/2021数学１,数学Ａ

第３問(4)

解答欄コ，サ，シ，スセ

小問(4)のうち、解答欄コ，サ，シ，スセに関する問題です。

解答欄コ，サ，シ，スセ

$B \ , \ C$ の少なくとも一方があたりのくじを引く事象 $E_{2}$ の確率

2017年センター試験１・Ａ第３問(4) — 第３問(4) 解答欄コ，サ，シ，スセ

小問(2)と似たような形式なので、同じようにして解くことができます。３つの問がありますが、上から順に誘導に従って解いていきましょう。

「Ｂ，Ｃの少なくとも一方があたりのくじを引く」ときの結果を書き出します。

「Ｂ，Ｃの少なくとも一方があたりのくじを引く」事象

$B \ , \ C$ の少なくとも一方があたりのくじを引く事象を書き出すと

（$A \ , \ B \ , \ C$）＝（当，当，は），（当，は，当），（は，当，当），（は，当，は），（は，は，当）

の $5$ 通りある。

全部で５通りあります。

選択肢を見ると「はずれ」の文言が出てきているので、はずれに注目しながら結果を見ていきます。すると以下のようなことが分かります。

はずれに注目すると分かること

（は，当，当），（は，当，は），（は，は，当）：「Ａがはずれを引く事象」に対応
（当，当，は）：「Ｂだけがはずれを引く」事象に対応
（当，は，当）：「Ｃだけがはずれを引く」事象に対応

ここで注意したいのは、「Ａが」と「Ａだけが」では意味が異なるということです。「Ａが」とある場合、Ａ以外のＢやＣのことを考える必要があります。ここは読解力が必要な場面です。

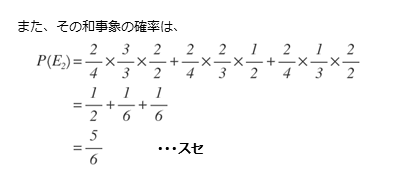
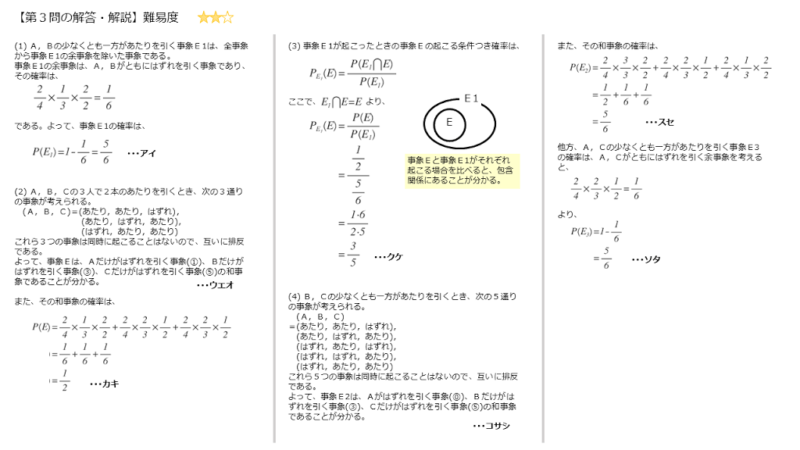
これら３つの事象は互いに排反であると言えるので、この３つの事象の和事象が事象Ｅ₂であることが分かります。

解答欄コ，サ，シの解答例をまとめると以下のようになります。

また、３つの事象の確率を求めて和を取れば、和事象の確率、つまり事象Ｅ₂の確率を求めることができます。

解答欄スセの解答例をまとめると以下のようになります。

解答欄ソタ

小問(4)の最後は解答欄ソタに関する問題です。

解答欄ソタ

$A \ , \ C$ の少なくとも一方があたりのくじを引く事象 $E_{3}$ の確率

この問題もこれまでと同じようにして求めるか、余事象を利用して求めます。スピードを求めるなら余事象ですが、小問(5)のことを考えて結果を書き出しておくと良いでしょう。

「Ａ，Ｃの少なくとも一方があたりのくじを引く」ときの結果を書き出します。

「Ａ，Ｃの少なくとも一方があたりのくじを引く」事象

$A \ , \ C$ の少なくとも一方があたりのくじを引く事象を書き出すと

（$A \ , \ B \ , \ C$）＝（当，当，は），（当，は，当），（は，当，当），（当，は，は），（は，は，当）

の $5$ 通りある。

結果を書き出すと５通りあることが分かります。これらの結果が出てくる事象は、同時に起こることはないので互いに排反です。

このことから、各事象の和事象が事象Ｅ₃になります。また、その確率は５つの排反な事象の確率の和になります。

解答欄ソタの解答例をまとめると以下のようになります。

第３問(1)～(4)のポイントと解答例をまとめると以下のようになります。

第３問(5)

解答欄チ

小問(5)は解答欄チに関する問題です。

解答欄チ

$3$ つの条件付き確率 $p_{1} \ , \ p_{2} \ , \ p_{3}$ を求め、それらの値の大小を比較する問題

３つの条件付き確率ｐ₁，ｐ₂，ｐ₃の値の大小を比較する前に、これらのことを確認しておきます。

３つの条件付き確率ｐ₁，ｐ₂，ｐ₃ について

条件付き確率ｐ₁：事象Ｅ₁が起こったときの事象Ｅの起こる条件付き確率
条件付き確率ｐ₂：事象Ｅ₂が起こったときの事象Ｅの起こる条件付き確率
条件付き確率ｐ₃：事象Ｅ₃が起こったときの事象Ｅの起こる条件付き確率

事象Ｅ₁が起こったときの事象Ｅの起こる条件付き確率ｐ₁については、小問(3)ですでに求めています。

残り２つの条件付き確率ｐ₂，ｐ₃も、同じようにして共通部分を考えてから公式で求めます。

共通部分を考えるために、事象Ｅ，Ｅ₁，Ｅ₂，Ｅ₃について結果を書き出して並べると、次のようになります。

書き並べてみると分かるように、事象Ｅは、事象Ｅ₁，Ｅ₂，Ｅ₃にそれぞれ含まれています。つまり、どの共通部分も事象Ｅに等しいことが分かります。

各共通部分の確率は、それぞれの条件付き確率の分子になるものです。共通部分がすべて事象Ｅに等しくなるということは、分子はすべて等しくなります。

分子が等しいとき、分母の値によって大小を調べることができますが、ここでは３つの条件付き確率をそれぞれ求めて値の大小を比較します。

解答欄チの解答例をまとめると以下のようになります。

条件付き確率を求めるとき、解答例のように確率を用いて計算することがあります。この計算では分数の中に分数が出てくるので、計算ミスをしやすいかもしれません。

ですから、場合の数がすでに分かっていれば、場合の数を積極的に用いた方が計算が楽になります。

条件付き確率の公式

事象 $A$ が起こったときの事象 $B$ が起こる条件付き確率 $P_{A}(B)$ は

\begin{align*} \quad P_{A}(B) &= \frac{n \left(A \cap B \right)}{n \left( A \right)} \\[ 7pt ] &= \frac{P \left(A \cap B \right)}{P \left( A \right)} \end{align*}

条件付き確率 $P_{A}(B)$ は、事象 $A$ が全事象になり、その事象 $A$ の中で共通部分となる事象 $A \cap B$ が起こる確率を求めたもの。

第３問(5)のポイントと解答例をまとめると以下のようになります。

従来の「場合の数と確率」の問題と第３問の比較

「場合の数と確率」に関する問題は、例年ならば「具体的で易しい問題から、抽象的で複雑な問題へ」という構成で、徐々に難易度が上がるイメージがありました。

しかし、小問(1)～(4)が最後の小問(5)を考えるための布石のような構成になっており、場合によっては小問(2)くらいから躓いてしまう可能性がありました。

また、結果を漏れなく書き出し、それをもとに確率を求めるだけでなく、用語の意味を正しく理解しているかも問われた問題でした。ですから、暗記に頼った学習では手も足も出せなかった可能性があります。

何事も覚えることから始まるが、理解につなげる学習を。「暗記でどうこうできるほど甘くない」ということを肝に銘じておこう。

なお、結果を書き出すことは基本的に最後の手段であることが多いので、結果を書き出さずに解き始めた人もいるかもしれません。

条件付き確率を求めるときになって、結果を書き出す必要があることに気付きますが、最初から書き出していた方が全体的にはスムーズに解けたでしょう。

結果を書き出すかどうかは、すべての場合の数を考えれば判断できます。すべての場合の数が少なければ書き出した方が良いでしょう。

教科書で確認しておきたい知識

「排反」とは、２つの事象が同時に起こらないこと。
排反である２つの事象を含む事象は、和事象となる。
和事象の確率は、排反である２つの事象の確率の和で求めることができる。
条件付き確率を求めるとき、共通部分の事象の確率を考えること。

Recommended books

さいごのセンター試験では、共通テストを意識した問題が出題されていました。これまでに見慣れない形式での出題がいくつか見られました。

難易度に関して言えば、これまでのセンター試験とそれほど変わりません。しかし、出題形式に変化があれば、思った以上に難しく感じるものです。実際、2020年の数学の平均点は前年よりも下がっているので、難しく感じた受験生が多かったと考えられます。

傾向の変化に対応するためには、やはり「解き慣れる」ことでしょう。色んなレベルや形式の問題をこなすことが一番の近道です。