数学1・A|2017センター試験・第4問を解いてみよう

第4問(3)

(3)では、具体的な数を用いて、約数や倍数のことについて考える問題になっています。これらと因数(素因数)との関係を理解しているかがポイントになります。
また、2進法への変換のやり方についても問われています。
解答欄シス
(3)の解答欄シスに関する問題です。
解答欄シス
$1188$ の正の約数の個数

正の約数の個数に関する問題です。扱う数が1桁や2桁など桁の少ない数であれば、じかに約数を求めてその個数を数えることができます。
しかし、1188のように桁の多い数になると、約数を求めるのが面倒です。正の約数の個数と言えば、素因数分解後の指数を利用して求めます。
正の約数の個数
自然数 $x$ が素因数 $a \ , \ b$ を用いて
\begin{align*} \quad x={a}^{m} \times {b}^{n} \end{align*}で表されるとき、自然数 $x$ の正の約数の個数は
\begin{align*} \quad \left(m+1 \right) \times \left(n+1 \right) \end{align*}この公式を利用するために、1188を素因数分解します。1188が4の倍数でもあり、9の倍数でもあることに注目して分解します。
1188を素因数分解する
$1188$ が素因数分解すると
\begin{align*} \quad 1188 &= 36 \times 33 \\[ 7pt ] &= 4 \times 9 \times 3 \times 11 \\[ 7pt ] &= {2}^{2} \times {3}^{3} \times 11 \end{align*}1188が素因数2,3,11の積で表されることが分かりました。累乗の指数をもとに、正の約数の個数を求めます。
1188の正の約数の個数を求める
\begin{align*} \quad 1188 = {2}^{2} \times {3}^{3} \times 11 \end{align*}であるので、$1188$ の正の約数の個数は
\begin{align*} &(2+1) \times (3+1) \times (1+1) \\[ 7pt ] = \ &3 \times 4 \times 2 \\[ 7pt ] = \ &24 \ \text{(個)} \end{align*}解答欄シスの解答例をまとめると以下のようになります。
正の約数の個数について
ある自然数の正の約数の個数は、先ほどの公式で求めるのが一般的です。なぜあのような公式が得られるのかを考えてみましょう。
ある自然数xを素因数分解すると、素因数a,bを用いてx=am×bnで表されたとします。
このとき、自然数xの正の約数は、素因数aやbからできているはずです。ですから、正の約数は素因数a,bの組合せを考えれば良いことが分かります。
イメージをはっきりさせるために、たとえば、12の正の約数を考えてみましょう。
参考 12の正の約数
$12$ の約数は、$1 \ , \ 2 \ , \ 3 \ , \ 4 \ , \ 6 \ , \ 12$ の $6$ 個。
ここで
\begin{align*} \quad 12={2}^{2} \times 3 \end{align*}より、素因数は $2 \ , \ 3$ を用いて $12$ の正の約数を表すと
\begin{align*} \quad 1 &= {2}^{0} \times {3}^{0} \\[ 7pt ] 2 &= {2}^{1} \times {3}^{0} \\[ 7pt ] 3 &= {2}^{0} \times {3}^{1} \\[ 7pt ] 4 &= {2}^{2} \times {3}^{0} \\[ 7pt ] 6 &= {2}^{1} \times {3}^{1} \\[ 7pt ] 12 &= {2}^{2} \times {3}^{1} \end{align*}これより、約数は素因数の累乗で表されることが分かる。
また、これらを指数に注目して並び替えると
\begin{align*} \quad {2}^{0} \times {3}^{0} &= 1 \\[ 7pt ] {2}^{0} \times {3}^{1} &= 3 \\[ 7pt ] {2}^{1} \times {3}^{0} &= 2 \\[ 7pt ] {2}^{1} \times {3}^{1} &= 6 \\[ 7pt ] {2}^{2} \times {3}^{0} &= 4 \\[ 7pt ] {2}^{2} \times {3}^{1} &= 12 \end{align*}$2$ の累乗は $0 \ , \ 1 \ , \ 2$ 乗の $3$ 通りあり、それらに対して $3$ の累乗が $0 \ , \ 1$ 乗の $2$ 通りずつあることが分かる。
積の法則から、正の約数の個数は全部で
\begin{align*} \quad 3 \times 2 = 6 \ \text{(個)} \end{align*}以上から、約数は、指数の選び方を考えれば作ることができる。
12の約数の場合を参考にすると、自然数xがx=am×bnに素因数分解されるとき、素因数a,bの累乗の作り方はそれぞれ以下のようになります。
素因数a,bの選び方
- 素因数aの累乗の作り方:a0,a1,…,am の(m+1)通り
- 素因数bの累乗の作り方:b0,b1,…,bn の(n+1)通り
このことから、約数の作り方は、素因数aの累乗の作り方の(m+1)通りのそれぞれに対して、素因数bの累乗の作り方が(n+1)通りずつあります。
場合の数で学習した積の法則を利用すると、正の約数の個数は全部で (m+1)(n+1) 個になります。
自然数の正の約数の個数は、積の法則を用いた場合の数で得られる個数。
(1)~(3)の解答欄シスまでのポイントと解答例をまとめると以下のようになります。
解答欄セソ,タ
(3)の解答欄セソ,タに関する問題です。
解答欄セソ,タ
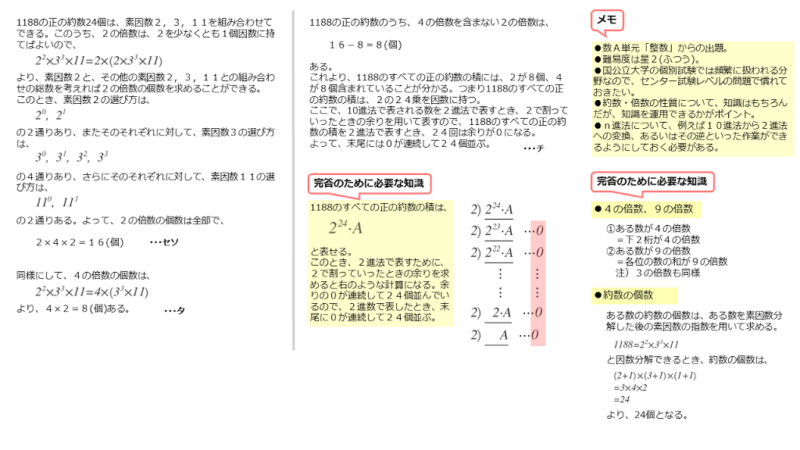
$1188$ の正の約数のうち、$2$ の倍数と $4$ の倍数の個数

解答欄シスに関する問題で求めた結果から、1188の正の約数は全部で24個です。このうち、2の倍数や4の倍数になるものの個数を求めます。
2の倍数である条件と4の倍数である条件は以下の通りです。
2の倍数である条件、4の倍数である条件
- 2の倍数になる数 … 素因数2を少なくとも1つもつ
- 4の倍数になる数 … 素因数2を少なくとも2つ以上もつ
これを参考にして、1188を素因数分解した式を少し変形します。
1188を素因数分解した式を変形する
\begin{align*} \quad 1188 &= {2}^{2} \times {3}^{3} \times 11 \\[ 7pt ] &= 2 \times \left(2 \times {3}^{3} \times 11 \right) \quad \cdots \text{①} \\[ 7pt ] &= 4 \times \left({3}^{3} \times 11 \right) \quad \cdots \text{②} \end{align*}①式は $2$ の倍数を表し、②式は $4$ の倍数を表す。
2の倍数となる数は、①式においてカッコ内の素因数2,3,11の累乗の選び方で決まります。同じように、4の倍数となる数は、②式においてカッコ内の素因数3,11の累乗の選び方で決まります。
2の倍数の個数から求めます。
2の倍数の個数を求める
\begin{align*} \quad 1188 &= {2}^{2} \times {3}^{3} \times 11 \\[ 7pt ] &= 2 \times \left(2 \times {3}^{3} \times 11 \right) \quad \cdots \text{①} \\[ 7pt ] &= 4 \times \left({3}^{3} \times 11 \right) \quad \cdots \text{②} \end{align*}①式において、素因数 $2$ に対して、残りの素因数の選び方は
\begin{align*} &\quad {2}^{0} \ , \ {2}^{1} \ \text{の $2$ 通り} \\[ 7pt ] &\quad {3}^{0} \ , \ {3}^{1} \ , \ {3}^{2} \ , \ {3}^{3} \ \text{の $4$ 通り} \\[ 7pt ] &\quad {11}^{0} \ , \ {11}^{1} \ \text{の $2$ 通り} \end{align*}よって、$2$ の倍数の個数は積の法則から
\begin{align*} \quad 2 \times 4 \times 2=16 \ \text{(個)} \end{align*}解答欄セソの解答例をまとめると以下のようになります。
同じ要領で4の倍数の個数を求めます。
4の倍数の個数を求める
\begin{align*} \quad 1188 &= {2}^{2} \times {3}^{3} \times 11 \\[ 7pt ] &= 2 \times \left(2 \times {3}^{3} \times 11 \right) \quad \cdots \text{①} \\[ 7pt ] &= 4 \times \left({3}^{3} \times 11 \right) \quad \cdots \text{②} \end{align*}②式において、因数 $4$ に対して、残りの素因数の選び方は
\begin{align*} &\quad {3}^{0} \ , \ {3}^{1} \ , \ {3}^{2} \ , \ {3}^{3} \ \text{の $4$ 通り} \\[ 7pt ] &\quad {11}^{0} \ , \ {11}^{1} \ \text{の $2$ 通り} \end{align*}よって、$4$ の倍数は積の法則から
\begin{align*} \quad 4 \times 2=8 \ \text{(個)} \end{align*}解答欄タの解答例をまとめると以下のようになります。
解答欄チツ
(3)の解答欄チツに関する問題です。
解答欄チツ
$1188$ のすべての正の約数の積を $2$ 進法で表すと、末尾に連続して並ぶ $0$ の個数

日頃から使っている数は10進法の数です。2進法などの他のルールで数を表すには、表し方のルール(記数法)を知っておく必要があります。
10進法とは0,1,…,9の10個の数を用いて、数を表す方法のこと。
10進法の数を2進法で表す方法は、数の素因数分解に似ています。
10進法で表される数を2進法で表す
素因数分解と同じ要領ですが、つねに2で割っていきます。このときの余りを求めていき、その余りを順に並べると2進法の数に置換することができます。
10進法から2進法への変換のやり方が分かったところで、1188のすべての正の約数の積を考えます。ただし、2進法に変換するとき、2で割っていくことと、連続する0の個数を考えることに注目しながら考えます。
2進法に変換するとき0が出てくるのは、2で割ったとき余りが0のときです。
このことから、1188のすべての正の約数の積が2を因数にもつ限り、2で割ったときの余りは0になります。ですから、1188の正の約数のうち、2の倍数や4の倍数に注目すれば良いことが分かります。
1188の正の約数のうち、2の倍数は24個あります(解答欄セソ)。また、4の倍数は8個あります(解答欄タ)。
これらから、1188のすべての正の約数の積には、2の倍数が24個、4の倍数が8個含まれています。
ここで注意しなければならないのは、2の倍数の中に4の倍数が含まれていることです。2の倍数と4の倍数の重複ぶんを考慮して、2の個数を調べます。
2の倍数や4の倍数のもつ因数2の個数
$2$ の倍数のうち、$4$ の倍数でない数は
\begin{align*} \quad 24-8=16 \ \text{(個)} \end{align*}これらは $2$ を $1$ 個ずつ因数にもつ。
また、$4$ の倍数は $8$ 個あるが、これらは $2$ を $2$ 個ずつ因数にもつ。
よって、$2$ は全部で
\begin{align*} \quad 8 \times 2=16 \ \text{(個)} \end{align*}したがって、1188のすべての正の約数の積は
\begin{align*} \quad 8+16=24 \ \text{(個)} \end{align*}の $2$ を因数にもつ。
1188のすべての正の約数の積には、素因数2が24個含まれているので、2進法に変換したとき、余り0が連続するのは24回になります。したがって、末尾に0が連続して24個並ぶことになります。
2の倍数の個数24個と4の倍数の個数8個を単純に足さないように気を付けよう。2の倍数と4の倍数との包含関係を考えよう。
解答欄チツの解答例をまとめると以下のようになります。
10進法から2進法への変換のやり方です。素因数分解と同じ要領ですが、必ず2で割っていき、余りを求めます。
(3)の解答欄タまでは完答できる基礎レベルの問題でした。最後の解答欄チツに関する問題は面喰いますが、それまでの問題も考慮に入れて考えれば解けなくはないレベルです。
解答欄セソからタチまでのポイントと解答例をまとめると以下のようになります。
「整数の性質」に関する問題では、不定方程式やユークリッドの互除法を扱った問題の方が頻出でしたが、今回は約数や倍数とその個数やn進法を扱った問題でした。
面喰ったり、難しく感じたりしたかもしれませんが、よく理解していないと解けない点で第4問も良問だったと思います。
傾向を把握しておくべきだが、傾向に縛られ過ぎないようにしよう。あらゆる出題を想定して、履修内容をしっかり網羅しておこう。
Recommended books
先日、英語の民間検定試験導入に変更があった大学共通テスト。今後も内容が変更される可能性があるので、こまめに情報収集しておきたいところです。
数学でも記述問題が導入されますが、センター試験と本質的には変わりません。共通テストであっても誘導形式に沿って解くので、大筋ではほとんど変わりません。
また、数学ではどんな問題でも基本的に過程を無視して解くことはできません。つまり、記述しながら解くことは、共通テストに限らず、日常的に行います。日常学習で意識的に取り組んでいれば、記述の訓練は特別に必要ありません。
ただ、共通テストの傾向は知っておいて損はありません。傾向を知り、それに合わせて準備する。このことは時間を掛ければ掛けるほど効果的です。ここでは、傾向と対策のための教材を紹介します。
オススメ 『大学入学共通テスト 数学予想問題集』シリーズ
共通テストにおける数学の傾向は、これまでに実施されたプレテストを分析することで掴むことができます。あくまでも傾向なので、確実に当たるわけではありません。しかし、出題者の意図からどのような問題が出題されそうかは、対策する上でとても役立ちます。
日常学習でも「記述問題に出題されそうだ」などと自分なりに考えながら取り組むことが大切です。
共通テスト対策として必要なことをすべて備えた理想の予想問題集が完成
単に問題を解くだけでなく、その背景にある考え方や知識まで掘り下げて解説。「分析編」では、過去2回の試行調査(プレテスト)から見えてきた共通テストの出題傾向を詳細に分析するだけでなく、学習法や学習姿勢などの具体的な対策まで説明。本番でそのまま出そうな予想問題と、くわしい解説がセットになった至高の実践型問題集。
もくじ
- 本冊
- 分析編
- 解答・解説編
- 別冊
- 試行調査:2回分(2017年度/2018年度)
- 予想問題:2回分
公式サイトでは、一部の内容を閲覧できます。
KADOKAWAの公式サイト
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
教科書で確認しておきたい知識
- 4の倍数は、下2桁が4の倍数である数。
- 9の倍数は、各位の和が9の倍数である数。
- 正の約数の個数は、素因数分解後の指数を利用して求める。
- 約数は、素因数(因数)の組合せによって得られる。
- 10進法 ⇔ 2進法の置換のやり方をマスターしておく。