図形と計量｜三角比の相互関係についてその１

04/21/2022数学１

三角比の相互関係を扱った問題を実際に解いてみよう

次の問題を解いてみましょう。

三角比の相互関係を利用できる形に気づくことが大切です。

問１の解答・解説

問１

次の式を簡単にせよ。

\begin{align*} \quad \left(\sin \theta + \cos \theta \right)^{2} + \left(\sin \theta – \cos \theta \right)^{2} \end{align*}

与式を観察すると、このままでは三角比の相互関係を利用できそうにありません。利用できるのは、乗法公式で展開してからになりそうです。

与式を展開して同類項を整理します。

問１の解答例

\begin{align*} \quad &\left( \sin \theta + \cos \theta \right)^{2} + \left( \sin \theta – \cos \theta \right)^{2} \\[ 7pt ] = \ &\left(\sin \theta \right)^{2} + 2 \cdot {\sin \theta} \cdot {\cos \theta} +\left(\cos \theta \right)^{2} + \left(\sin \theta \right)^{2} – 2 \cdot {\sin \theta} \cdot {\cos \theta} +\left(\cos \theta \right)^{2} \\[ 7pt ] = \ &\sin^{2} \theta + 2 {\sin \theta}{\cos \theta} + \cos^{2} \theta + {\sin^{2} \theta} – 2 {\sin \theta}{\cos \theta} + \cos^{2} \theta \\[ 7pt ] = \ &2 \sin^{2} \theta + 2 \cos^{2} \theta \\[ 7pt ] = \ &2 \left(\sin^{2} \theta + \cos^{2} \theta \right) \end{align*}

ここで

\begin{align*} \quad \sin^{2} \theta + \cos^{2}=1 \end{align*}

より

\begin{align*} \quad &\left( \sin \theta + \cos \theta \right)^{2} + \left( \sin \theta – \cos \theta \right)^{2} \\[ 7pt ] =\ &2 \left(\sin^{2} \theta + \cos^{2} \theta \right) \\[ 7pt ] =\ &2 \cdot 1 \\[ 7pt ] =\ &2 \end{align*}

正弦と余弦の相互関係を表す式まで変形できました。正弦と余弦の相互関係を利用すると与式の値を求めることができます。

問１のポイントと解答例をまとめると以下のようになります。

与式を展開すると、累乗の形が出てくる。指数を付ける位置に気を付けよう。

結果が決まっている展開は覚えてしまおう

問１のような、正弦と余弦の和を２乗する計算はこれからも頻繁に出てきます。

出てくるたびに素直に展開していては面倒なので、結果を覚えてしまった方が今後ラクになります。

覚えておくとラクになる展開

\begin{align*} \quad \left( \sin \theta + \cos \theta \right)^{2} &= 1 +2 \ {\sin \theta} \ {\cos \theta} \\[ 7pt ] \quad \left( {\sin \theta} \ – \cos \theta \right)^{2} &= 1 -2 \ {\sin \theta} \ {\cos \theta} \end{align*}

詳しい導出は以下を参考にして下さい。

問２の解答・解説

問２

次の式を簡単にせよ。

\begin{align*} \quad \cos \theta \left(\sin \theta \tan \theta + \cos \theta \right) \end{align*}

与式を観察すると、３つの三角比が登場しています。方針としては２つ考えられます。

問２の方針

展開し、その後に相互関係を利用する
最初に相互関係を利用し、その後に展開する

三角比の相互関係を利用するのが先か後かの問題です。今回は、前者の方針を採用して解いてみましょう。

まず、与式を分配法則で展開します。

問２の解答例 1⃣

\begin{align*} \quad &{\cos \theta} \ {\left( {\sin \theta} \ {\tan \theta} + \cos \theta \right)} \\[ 7pt ] = \ &{\cos \theta} \cdot {\sin \theta} \cdot {\tan \theta} + \left( \cos \theta \right)^{2} \end{align*}

次に、三角比の相互関係を利用します。

問２の解答例 2⃣

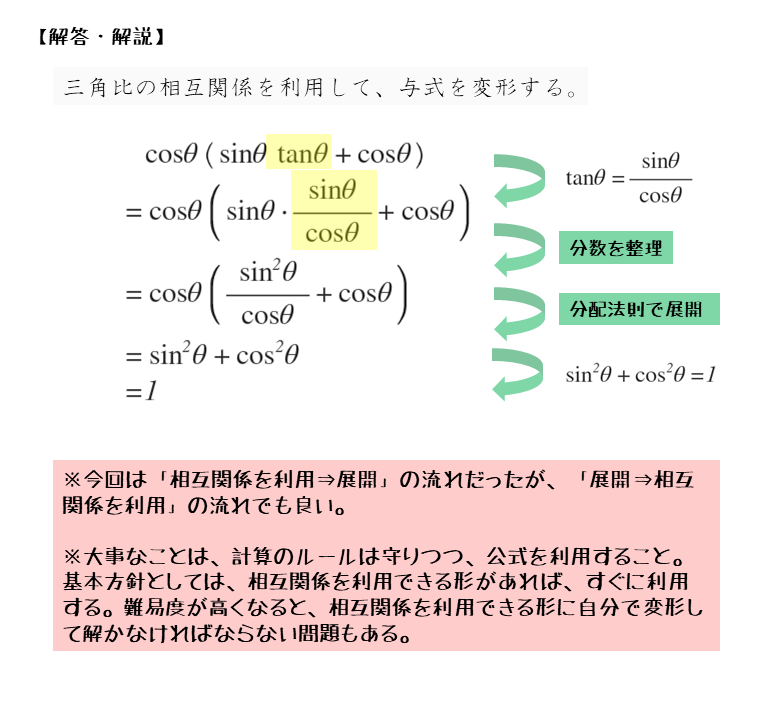
\begin{align*} &\vdots \\[ 7pt ] = \ &{\cos \theta} \cdot {\sin \theta} \cdot {\tan \theta} + \left( \cos \theta \right)^{2} \\[ 7pt ] = \ &{\cos \theta} \cdot {\sin \theta} \cdot \left( \frac{\sin \theta}{\cos \theta} \right) + \left( \cos \theta \right)^{2} \\[ 7pt ] = \ &\left( \sin \theta \right)^{2}+ \left( \cos \theta \right)^{2} \\[ 7pt ] = \ &\sin^{2} \theta + \cos^{2} \theta \end{align*}

ここで

\begin{align*} \quad \sin^{2} \theta + \cos^{2}=1 \end{align*}

より

\begin{align*} \quad &\left( \sin \theta + \cos \theta \right)^{2} + \left( \sin \theta – \cos \theta \right)^{2} \\[ 7pt ] =\ &\sin^{2} \theta + \cos^{2} \theta \\[ 7pt ] =\ &1 \end{align*}

さいごに、正弦と余弦の相互関係を利用して終了です。

最初に三角比の相互関係を利用した解答例とポイントをまとめると以下のようになります。

方針がいくつか挙がったとき、どちらを採用するかによって解答までの時間が異なります。どちらを選べば良いかは、実際に解いた経験がないと決められないでしょう。

時間制限のある試験では、どちらを採用するかで合否が決まることもあり得ます。

適切な方針で解けるように、実際に解いておくことが大切です。そして、本番で迷わないように、自分なりに問題に対する方針を予め決めておきましょう。

Recommended books

図形の問題は、気付けないと全くと言って良いほど手も足も出なくなります。気付けるかどうかはやはり日頃から作図したり、図形を色んな角度から眺めたりすることだと思います。

そのためにもやはり演習量は大切です。はじめのうちは何事も質よりも量の方を意識してこなす方が良いと思います。全体を一度通ってから質を考えると効率が良いでしょう。

演習をこなすとなると、単元別になった教材を使って集中的にこなすと良いでしょう。網羅型でも良いですが、苦手意識のある単元であれば、単元別に特化した教材の方が良いかもしれません。

オススメその１

分野ごとに押さえていくのに役立つのは『高速トレーニング』シリーズです。三角関数、ベクトル、数列などの分野もあります。

ここで紹介するのは『数学１高速トレーニング三角比編』です。

三角比に苦手意識のある人にとって、躓きやすいところを解説してあるので良い教材だと思います。基礎の定着に向いた教材です。

これで自信がついたら、チャートなどのもう少し難易度の高い問題を扱った教材に取り組むと良いでしょう。三角比は三角関数に関わるので、ここでしっかりマスターしておきましょう。

数学１高速トレーニング三角比編

created by Rinker

オススメその２

『改訂版坂田アキラの三角比・平面図形が面白いほどわかる本』もおすすめです。

計算過程が省略されず、丁寧に記述されているので、計算の途中で躓くこともほとんどないでしょう。苦手な人や初学者にとって良い補助教材になると思います。

坂田のビジュアル解説で最近流行りの空間図形までフォロー!

数学１「図形と計量」（いわゆる三角比）と数学Ａ「図形の性質」の基本事項をまとめ、それぞれの典型問題および融合問題の考え方・解き方がていねいに解説されています。

また、今回の改訂により、近年の大学入試（上位から下位まで幅広く）で頻出の空間図形の問題を厚くしました。