図形の性質｜重心について
重心を扱った問題を解いてみよう
次の問題を考えてみましょう。
問１の解答・解説
問１
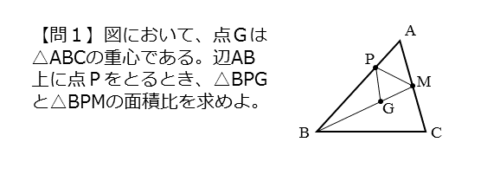
図において、点 $G$ は $\triangle {ABC}$ の重心である。辺 $AB$ 上に点 $P$ をとるとき、$\triangle {BPG}$ と $\triangle {BPM}$ の面積比を求めよ。
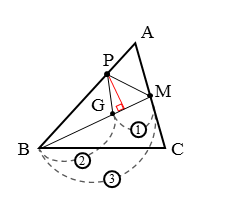
問１では、△ＢＰＧと△ＢＰＭの面積比を求めます。
△ＢＰＧと△ＢＰＭにおいて、底辺をそれぞれＢＧ，ＢＭとすると、頂点Ｐから下した垂線の長さが高さとなります。ですから、△ＢＰＧと△ＢＰＭは高さが等しい三角形となります。
このことに気付けば、（面積比）＝（底辺の比）を利用する方針が思い浮かぶでしょう。この関係から、△ＢＰＧと△ＢＰＭの面積比を求めるには、線分ＢＧと線分ＢＭの比を考えれば良いことが分かります。
一般に、１つの三角形を２つの三角形に分割した図形の場合、高さが等しくなる。高さが等しければ（面積比）＝（底辺比）を利用できる。
線分ＢＭは重心Ｇを通るので中線です。重心の性質から、重心Ｇは線分ＢＭを２：１に内分します。この内分比を利用すれば、ＢＧとＢＭの比を求めることができます。
問１の解答例 1⃣
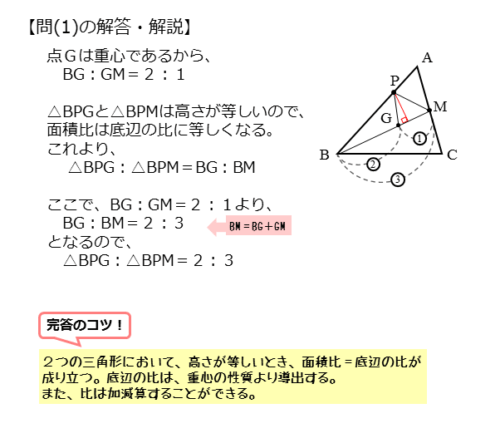
$\triangle {BPG}$ と $\triangle {BPM}$ の高さはともに等しいので
\begin{align*} \quad \triangle {BPG} : \triangle {BPM} = BG: BM \end{align*}が成り立つ。
ここで
\begin{align*} \quad BG : GM = 2:1 \end{align*}より
\begin{align*} \quad BG : BM = 2 : 3 \end{align*}
底辺の比が面積比に等しいので、得られた比が面積比となります。
問１の解答例 2⃣
\begin{align*} &\vdots \\[ 7pt ] \quad BG &: BM = 2 : 3 \end{align*}したがって
\begin{align*} \quad \triangle {BPG} : \triangle {BPM} = 2: 3 \end{align*}問１のポイントと解答例をまとめると以下のようになります。
問２の解答・解説
問２
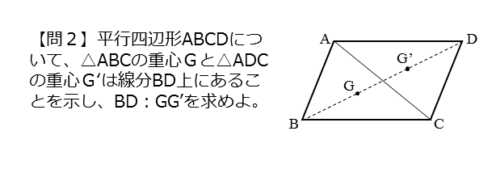
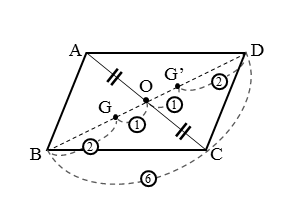
平行四辺形 $ABCD$ について、$\triangle {ABC}$ の重心 $G$ と $\triangle {ADC}$ の重心 $G’$ は線分 $BD$ 上にあることを示せ。また、$BD:GG’$ を求めよ。
問２では、２つの重心が同一線分上にあることを証明します。また、線分の比を求めます。
まず、△ＡＢＣの重心Ｇと△ＡＤＣの重心Ｇ’が線分ＢＤ上にあることを証明します。
重心を通る線分を考えてみると、そのような線分は中線以外に思いつきません。
２つの重心が線分ＢＤ上にあるということは、重心を通る中線も線分ＢＤ上にあるということです。
言い換えれば、中線が線分ＢＤに重なるということです。このことを示せないかを考えましょう。
図のように、平行四辺形の２つの対角線の交点をＯとおきます。平行四辺形の対角線ＡＣ，ＢＤは互いに他を二等分するという性質をもちます。
平行四辺形の対角線の性質
$2$ 本の対角線は互いに他を二等分するので
\begin{align*} \quad OA = OC \ , \ OB = OD \end{align*}（※図の平行四辺形を参照）
この対角線の性質から、点Ｏは線分ＡＣの中点になります。このとき、線分ＯＢは△ＡＢＣにおける中線になり、線分ＯＤは△ＡＤＣにおける中線になります。
線分ＯＢが中線であれば、△ＡＢＣにおいて重心Ｇは線分ＯＢ上にあると言えます。
同様に、線分ＯＤが中線であれば、△ＡＤＣにおいて重心Ｇ’は線分ＯＤ上にあると言えます。
さいごに、線分ＯＢ，ＯＤはともに線分ＢＤの一部であるので、重心Ｇ，Ｇ’は線分ＢＤ上にあることが示せます。
次に、ＢＤ：ＧＧ’を求めます。重心による中線の内分比を書き込めばすぐに分かります。
ここでは、ＯＢ＝ＯＤに注目して求めています。後述する記述例とは異なりますが、こんな答案もあることを知っておくと良いでしょう。
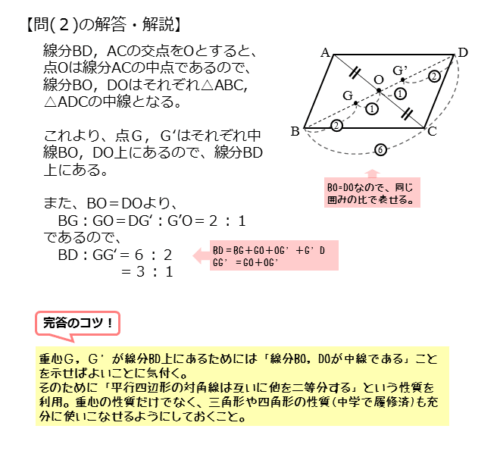
問２の解答例
$2$ 点 $G \ , \ G’$ は重心であるので
\begin{align*} \quad BG : GO = DG’ : G’O = 2:1 \end{align*}$OB = OD$ より
\begin{align*} \quad BG = DG’ \ , \ GO = G’O \end{align*}よって
\begin{align*} \quad BD : GG’ = \left(OB + OD \right) : \left(GO + G’O \right) \end{align*}また、$OB : GO = OD : G’O = 3 : 1$ より
\begin{align*} \quad OB = 3GO \ , \ OD = 3G’O \end{align*}よって
\begin{align*} \quad BD : GG’ &= \left(3GO + 3G’O \right) : \left(GO + G’O \right) \\[ 7pt ] &= 3\left(GO + G’O \right) : \left(GO + G’O \right) \end{align*}したがって
\begin{align*} \quad BD : GG’ = 3 : 1 \end{align*}線分の比を求めること自体はそれほど難しくありません。しかし、比を求める過程を記述するのは意外と難しいです。図形を扱った証明問題を多くこなしておいた方が良いでしょう。
問２のポイントと解答例をまとめると以下のようになります。
図形の証明問題では、図形の定義や性質を上手に利用する必要があります。図形の定義や性質をしっかり覚えておきましょう。
Recommended books
オススメその１
予習の際に理解が進めば授業のスピードについていくことができ、復習や課題をこなす時間も少なくて済みます。予習や復習の補助教材に向いている教材が『とってもやさしい数学』シリーズです。
とってもやさしい数学１・Ａでは２冊とも中学で学習した内容にも触れており、中学内容と高校内容とのつながりを把握しやすい教材です。
一学期のうちは不安を抱えながら学習を進めていく人も多いかと思います。スタートで躓かないためにも易しく取り組みやすい教材を使うのも一つのやり方です。無理をして内容の難しい教材を使うよりもはるかに良いでしょう。
基礎的な内容を扱っているので、数学が苦手な人でも取り組みやすくなっています。興味のある人はぜひ一読してみて下さい。
『高校とってもやさしい数学１・Ａ 改訂版 その１』は「数と式」「２次関数」の単元を扱っています。
『高校とってもやさしい数学１・Ａ 改訂版 その２』は「場合の数」「確率」「整数の性質」「図形の性質」「三角比」の単元を扱っています。
オススメその２
高校では記述する力がないと問題を解くのも一苦労です。一足飛びに答えが出てくるような問題が少ないので、過程を書き残していく必要があるからです。
そうは言っても答案の書き方に特化した教材はなかなか見当たらないので、模範解答を参考にしながら記述の仕方を身に付けていくのが一般的ではないかと思います。
ここで紹介する『総合的研究 記述式答案の書き方』は、答案の書き方を身に付けることができる教材です。数学の答案では一般的に因果関係を示しながら記述していきます。これは模範解答を読めば明らかです。
学習の際に「書く」ことを疎かにしなければ、因果関係を意識しながら学習する習慣が徐々に身に付いていきます。因果関係を理解することは、教科書や参考書を読むときはもちろん、入試の読解問題などに大いに役立ちます。
このように記述する能力は高校の学習において意外と大切な能力ですが、時間を掛けて身に付けていくものです。ですから、やみくもにやっていては時間の浪費になってしまいます。
その助けになるのが『総合的研究 記述式答案の書き方』ではないかと思います。他とはちょっと違ったアプローチで作成されているので、手を出しにくいかもしれませんが、個人的にはおすすめの教材です。
さいごに、もう一度、頭の中を整理しよう
- 中線は三角形の頂点と対辺の中点とを結ぶ線分。
- 重心は三角形の３本の中線の交点。
- 重心は中線を頂点の方から２：１に内分する。
- 重心を頂点にもつ３つの三角形は、面積が等しい。