図形の性質|メネラウスの定理、チェバの定理について

今回はメネラウスの定理とチェバの定理について学習しましょう。旧課程のセンター試験ではほとんど出題されませんでしたが、新課程ではよく出題される問題の1つになりました。
たとえば、2017年のセンター試験でも出題されています。ほぼ出題されると思って対策を立てておいた方が無難でしょう。
メネラウスの定理やチェバの定理を扱った問題は、図形を見るとすぐにピンとくるのが特徴です。図形と定理をセットで覚えるように心掛けましょう。
記事の画像が見辛いときはクリックすると拡大できます。
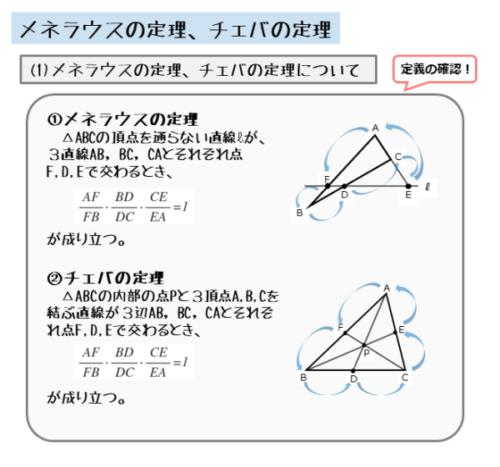
メネラウスの定理とチェバの定理
メネラウスの定理とチェバの定理は、三角形の3辺について、内分比や外分比によって得られる比の値の積が1になる定理です。
式を覚えるのはコツがあるので、それほど苦労しません。ただ、これらの定理が成り立つ図形を作図する方法や、定理を導出する方法を知っておくことは大切です。
メネラウスの定理やチェバの定理が成り立つ図形を作図しよう
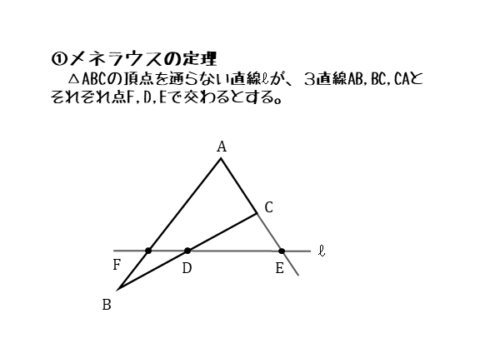
メネラウスの定理が成り立つ図形
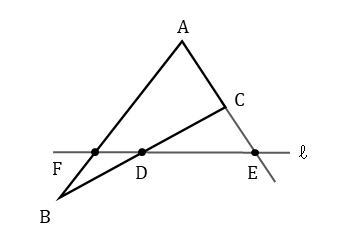
以下の手順でメネラウスの定理が成り立つ図形を作図します。
メネラウスの定理が成り立つ図形では、三角形の頂点を通る直線は出てきません。また、内分点だけでなく外分点が出てくるので注意が必要です。
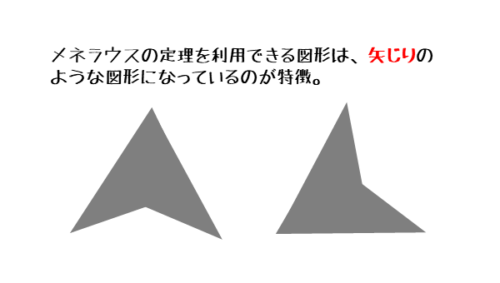
作図から分かるように、新たにできた内分点や外分点は同一直線上にあるのが特徴です。また、図形の見た目が矢じりのようになっているので、一目で気付くことができます。
メネラウスの定理なら、矢じり型の図形をイメージしよう。
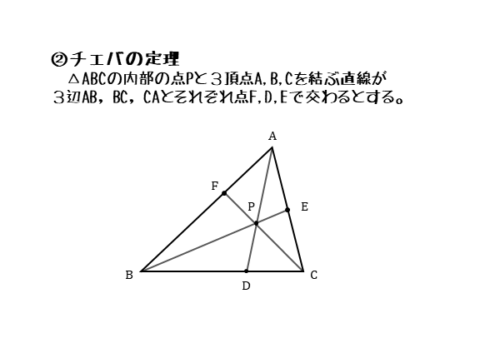
チェバの定理が成り立つ図形
以下の手順でチェバの定理が成り立つ図形を作図します。
チェバの定理が成り立つ図形の作図手順
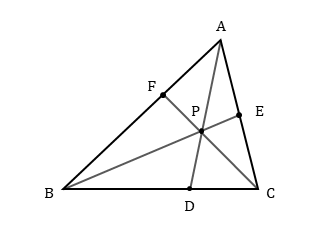
- 三角形の内部に点Pを1つとる。
- 内部の点Pと三角形の頂点A,B,Cとを通る直線AP,BP,CPをひき、辺と交点をつくる(内分点D,E,Fができる)。
三角形の内部にとった点Pは、内部ならどこでも構いません。作図から分かるように、三角形の内部に自分で点を先に作ってしまうので、外心や重心などの五心とはでき方が根本的に異なります。
特に、重心と混同する人がいるようですが、見た目は似ていても全く別物です。重心は3中線の交点ですが、上述の点Pはそうではありません。
メネラウスの定理の式を導出しよう
メネラウスの定理を表す式を導出してみましょう。式の成り立ちが分かれば立式しやすくなります。
平行線と線分の比の関係を利用しよう
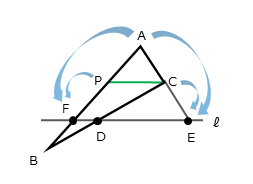
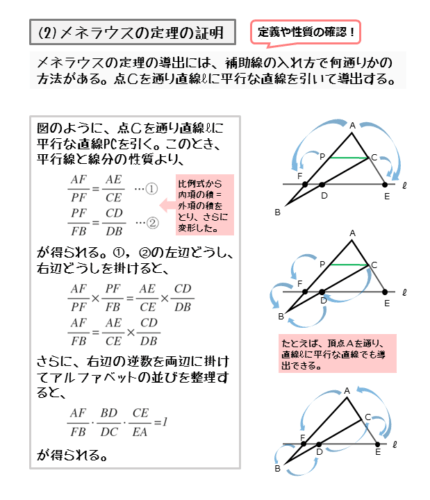
先ほどの図に補助線を加えます。点Cを通り、直線ℓに平行な直線を引き、この直線と辺ABとの交点をPとします。
定理の導出には様々な方法がありますが、ここでは平行線と線分の比の関係を利用します。この関係を利用すると比例式が得られます。さらに、この比例式から①式を導くことができます。
メネラウスの定理の導出 1⃣
点 $C$ を通り、直線ℓに平行な直線を引き、この直線と辺 $AB$ との交点を $P$ とする。
平行線と線分の比より
\begin{align*} \quad AF:PF &= AE:CE \\[ 7pt ] AF \cdot CE &= PF \cdot AE \\[ 7pt ] \frac{AF}{PF} &= \frac{AE}{CE} \quad \cdots \text{①} \end{align*}比が等しければ、比の値も等しくなることを知っていれば、わざわざ比例式から①式を導出する必要はありません。
他の線分に注目すると、同じようにして②式を導くことができます。
メネラウスの定理の導出 2⃣
同様にして、平行線と線分の比より
\begin{align*} \quad PF:FB &= CD:DB \\[ 7pt ] PF \cdot DB &= FB \cdot CD \\[ 7pt ] \frac{PF}{FB} &= \frac{CD}{DB} \quad \cdots \text{②} \end{align*}2つの等式を辺々掛けて整理しよう
平行線と線分の比を利用して、①,②式を導くことができました。
導出された①,②式
\begin{align*} \quad \frac{AF}{PF} &= \frac{AE}{CE} \quad \cdots \text{①} \\[ 7pt ] \frac{PF}{FB} &= \frac{CD}{DB} \quad \cdots \text{②} \end{align*}①,②式を辺々掛けて整理します。
2つの等式を辺々掛けるというのは、左辺どうし、右辺どうしをそれぞれ掛けるということです。なお、2つの式はともに等式なので、辺々掛けても等式は成り立ちます。
メネラウスの定理の導出 3⃣
\begin{align*} \quad \frac{AF}{PF} &= \frac{AE}{CE} \quad \cdots \text{①} \\[ 7pt ] \frac{PF}{FB} &= \frac{CD}{DB} \quad \cdots \text{②} \end{align*}①,②式を辺々掛けると
\begin{align*} \quad \frac{AF}{PF} \cdot \frac{PF}{FB} = \frac{AE}{CE} \cdot \frac{CD}{DB} \end{align*}すなわち
\begin{align*} \quad \frac{AF}{FB} = \frac{AE}{CE} \cdot \frac{CD}{DB} \end{align*}両辺を右辺で割ると
\begin{align*} \quad \frac{AF}{FB} \cdot \frac{DB}{CD} \cdot \frac{CE}{AE} = 1 \end{align*}したがって
\begin{align*} \quad \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1 \end{align*}辺々掛けたあとは、右辺が1になるように変形しています。最後はアルファベットの並びを整えて終了です。
左辺のアルファベットに注目しましょう。左側の分数から順に、分母⇒分子⇒分母…とアルファベットの並びが非常に特徴的であることに気付きます。その際、図形と合わせて見るともっと分かります。
メネラウスの定理
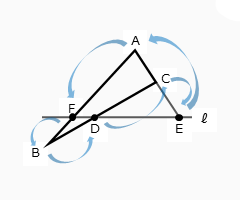
\begin{align*} \quad \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1 \end{align*}分母⇒分子⇒分母…の順に合わせて、頂点や内分点(外分点)を見ていくと、頂点と内分点(外分点)が交互になるように辿っていることが分かります。
そして、最終的には図形を1周するようにして元の頂点に戻ってきます。
このルールさえ守れば、頂点A以外からのスタートでも定理で表される式を導出することができます。しりとりのようになっているので、比較的覚えやすい式です。以上をまとめると以下のようになります。
頂点と内分点(外分点)を交互に辿りながら、1周して元の頂点に戻るように線分を選ぶのが立式のルール。ルールを守れば、定理で表された式以外でも成り立つことに注意しよう。
次は、チェバの定理を導出してみましょう。
チェバの定理の式を導出しよう
チェバの定理を表す式を導出してみましょう。
三角形の面積比と線分の比の関係を利用しよう
メネラウスの定理と同じように、チェバの定理の導出には様々な方法があります。ここでは面積比と線分の比の関係を利用します。
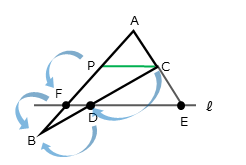
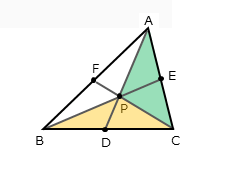
図のように、△ACPと△BCPに色を付け、これらの関係を表します。そのために、△ACFと△BCFの関係、△APFと△BPFの関係を考えます。
△ACFと△BCFは高さが等しい三角形なので、面積比は底辺の比に等しくなります。
チェバの定理の導出 1⃣
$\triangle ABC$ において、内部に点 $P$ を取る。
この点 $P$ と $3$ つの頂点 $A \ , \ B \ , \ C$ を通る直線と、辺 $AB \ , \ BC \ , \ CA$ との交点をそれぞれ $F \ , \ D \ , \ E$ とする。
$\triangle ACF$ と $\triangle BCF$ はともに高さが等しいので
\begin{align*} \quad \triangle ACF : \triangle BCF = AF : FB \end{align*}これより、実数 $m$ を用いて
\begin{align*} &\quad \triangle ACF = mAF \\[ 7pt ] &\quad \triangle BCF = mFB \end{align*}と表せる。
同じようにして、△APFと△BPFの面積も実数を用いて表します。
チェバの定理の導出 2⃣
同様に $\triangle APF$ と $\triangle BPF$ も実数 $n$ を用いて
\begin{align*} \quad \triangle APF &= nAF \\[ 7pt ] \quad \triangle BPF &= nFB \end{align*}と表せる。
以上をもとにして△ACPと△BCPの面積をそれぞれ求め、面積比を導きます。
チェバの定理の導出 3⃣
よって、$\triangle ACP$ と $\triangle BCP$ は
\begin{align*} \quad \triangle ACP &= \triangle ACF-\triangle APF \\[ 7pt ] \triangle BCP &= \triangle BCF-\triangle BPF \end{align*}であるので
\begin{align*} \quad \triangle ACP &=mAF-nAF \\[ 7pt ] \triangle BCP &= mFB-nFB \end{align*}整理すると
\begin{align*} \quad \triangle ACP &= \left(m-n \right)AF \\[ 7pt ] \quad \triangle BCP &= \left(m-n \right)FB \end{align*}したがって、$\triangle ACP$ と $\triangle BCP$ の面積比は
\begin{align*} \quad \triangle ACP : \triangle BCP=\left(m-n \right)AF : \left(m-n \right)FB \end{align*}すなわち
\begin{align*} \quad \triangle ACP : \triangle BCP= AF : FB \end{align*}△ACPと△BCPの面積比がAF:FBで表されることが分かりました。
ここで注意したいのは、線分AF,BFは、△ACP,△BCPの底辺でも高さでもないにもかかわらず、△ACP:△BCP=AF:FBが成り立つことです。
この関係を利用した問題が入試で出題されたことがあるので、図形と合わせて覚えておくと良いでしょう。
先ほどの面積比を表す比例式を変形すると、③式を導くことができます。
チェバの定理の導出 4⃣
\begin{align*} &\vdots \\[ 7pt ] \quad \triangle ACP &: \triangle BCP = AF : FB \end{align*}これより
\begin{align*} \quad FB \cdot \triangle ACP = AF \cdot \triangle BCP \end{align*}変形すると
\begin{align*} \quad \frac{\triangle ACP}{\triangle BCP} = \frac{AF}{FB} \quad \cdots \text{③} \end{align*}これと同じことが△ABPと△ACP、△BCPと△ABPの間にも成り立つので、④,⑤式が得られます。
チェバの定理の導出 5⃣
同様にして、$\triangle ABP$ と $\triangle ACP$ の面積比、$\triangle BCP$ と $\triangle ABP$ の面積比から
\begin{align*} \quad \frac{\triangle ABP}{\triangle ACP} &= \frac{BD}{DC} \quad \cdots \text{④} \\[ 7pt ] \quad \frac{\triangle BCP}{\triangle ABP} &= \frac{CE}{EA} \quad \cdots \text{⑤} \end{align*}3つの式を辺々掛けて整理しよう
③,④,⑤式を辺々掛けて整理します。
チェバの定理の導出 6⃣
③,④,⑤を辺々掛けると
\begin{align*} \quad \frac{\triangle ACP}{\triangle BCP} \cdot \frac{\triangle ABP}{\triangle ACP} \cdot \frac{\triangle BCP}{\triangle ABP} = \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} \end{align*}左辺を整理して
\begin{align*} \quad 1 = \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} \end{align*}したがって
\begin{align*} \quad \frac{AF}{FB} \cdot \frac{BD}{DC} \cdot \frac{CE}{EA} = 1 \end{align*}これでチェバの定理を表す式を導出することができました。
メネラウスの定理と同じように、頂点と内分点が交互になるように辿っています。そして、最終的には図形を1周するようにして元の頂点に戻ってきます。メネラウスの定理よりも分かりやすいので、覚えるのも早いでしょう。
以上をまとめると以下のようになります。
メネラウス定理とチェバの定理は、既習内容で導出できる定理。既習内容の復習や、式変形のテクニックなどを学べるので、積極的に定理や公式の導出に取り組もう。
次は、メネラウスの定理やチェバの定理を扱った問題を実際に解いてみましょう。