数学2
今回はパスカルの三角形について学習しましょう。
二項式の累乗を展開するときに利用できるのが、パスカルの三角形です。パスカルの三角形は中学でも少しだけ触れるので知っている人も多いかもしれません。
高校では、数列の単元でも扱われることがあります。性質を覚えておくと慌てずに済むでしょう。
パスカルの三角形をつくる
パスカルの三角形をつくるにあたって、以下の式を展開したときを考えます。
パスカルの三角形で用いられる二項式
\begin{equation*}
(a+b)^{\scriptsize{2}} \ , \ (a+b)^{\scriptsize{3}} \ , \cdots , \ (a+b)^{\scriptsize{5}} \ , \cdots
\end{equation*}
2つの文字a,bの二項からなる式を扱います。これらの項の係数はともに1であることに注意しましょう。
このような式を展開します。
二項式を展開する
\begin{align*}
(a+b)^{\scriptsize{1}} &= a+b \\[ 7pt ]
(a+b)^{\scriptsize{2}} &= a^{\scriptsize{2}} +2ab +b^{\scriptsize{2}} \\[ 7pt ]
(a+b)^{\scriptsize{3}} &= a^{\scriptsize{3}} +3a^{\scriptsize{2}}b +3ab^{\scriptsize{2}} +b^{\scriptsize{3}} \\[ 7pt ]
(a+b)^{\scriptsize{4}} &= a^{\scriptsize{4}} +4a^{\scriptsize{3}}b + 6a^{\scriptsize{2}}b^{\scriptsize{2}} +4ab^{\scriptsize{3}} +b^{\scriptsize{4}} \\[ 7pt ]
(a+b)^{\scriptsize{5}} &= a^{\scriptsize{5}} +5a^{\scriptsize{4}}b +10a^{\scriptsize{3}}b^{\scriptsize{2}} +10a^{\scriptsize{2}}b^{\scriptsize{3}} +5a^{\scriptsize{4}} +b^{\scriptsize{5}}
\end{align*}
それぞれの式を展開した後、各項の係数だけを取り出します。
各項の係数だけを取り出す
\begin{align*}
(a+b)^{\scriptsize{1}} &: \quad 1 \ , \ 1 \\[ 7pt ]
(a+b)^{\scriptsize{2}} &: \quad 1 \ , \ 2 \ , \ 1 \\[ 7pt ]
(a+b)^{\scriptsize{3}} &: \quad 1 \ , \ 3 \ , \ 3 \ , \ 1 \\[ 7pt ]
(a+b)^{\scriptsize{4}} &: \quad 1 \ , \ 4 \ , \ 6 \ , \ 4 \ , \ 1 \\[ 7pt ]
(a+b)^{\scriptsize{5}} &: \quad 1 \ , \ 5 \ , \ 10 \ , \ 10 \ , \ 5 \ , \ 1
\end{align*}
 パスカルの三角形
パスカルの三角形
取り出した係数を縦、横に順に並べると、三角形のようになることから、パスカルの三角形と言います。
パスカルの三角形の性質
パスカルの三角形をつくるために、毎回展開するのは面倒です。しかし、展開しなくても、パスカルの三角形の性質を覚えて於けば問題ありません。
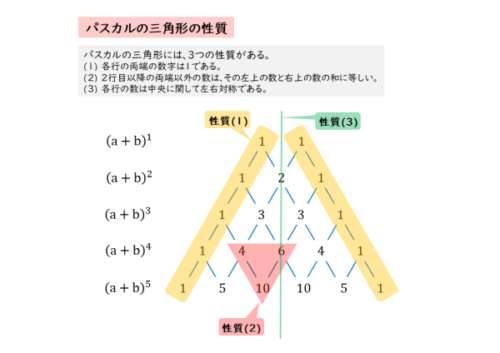
パスカルの三角形には3つの性質があります。
パスカルの三角形の性質
- 各行の両端の数字は1である。
- 2行目以降の両端以外の数は、その左上の数と右上の数の和に等しい。
- 各行の数は中央に関して左右対称である。
各行の両端の数字は必ず1になります。また、両端以外の数は、すぐ上の行の2つの数の和で求めることができます。
さらに、各行に並ぶ数は、中央に関して左右対称になるように並びます。この性質については、展開の公式を覚えるときに気付いた人もいるかもしれません。
 パスカルの三角形の性質
パスカルの三角形の性質
ここで学習するパスカルの三角形では、「二項からなり、かつ各項の係数が1である二項式」という条件がついていますが、ポイントは「各項の係数に一定の規則性がある」ことです。
このような係数の規則性は、この後に学習する「二項定理」や「多項定理」などにも見られるので、意識しながら学習すると覚えやすいでしょう。
おまけとして、3次式の因数分解を扱った問題を実際に解いてみましょう。
3次式の因数分解を扱った問題を解いてみよう
次の問題を解いてみましょう。
問
\begin{align*}
&\quad x^{\scriptsize{3}} +y^{\scriptsize{3}} = (x+y)^{\scriptsize{3}}-3xy(x+y) \\[ 7pt ]
&\text{であることを用いて} \\[ 5pt ]
&\quad x^{\scriptsize{3}} +y^{\scriptsize{3}} +z^{\scriptsize{3}} -3xyz \\[ 7pt ]
&\text{を因数分解せよ。}
\end{align*}
問の解答・解説
問は、与えられた条件式を用いて、3次式を因数分解する問題です。条件式は、式の値を求めるときによく用いられる式です。
式の値を求めるときによく用いられる式
\begin{equation*}
\quad x^{\scriptsize{3}} +y^{\scriptsize{3}} = (x+y)^{\scriptsize{3}}-3xy(x+y)
\end{equation*}
この式を用いて、与式を変形していきます。与式の1番目と2番目の項に注目すると、与えられた条件式の左辺と対応していることが分かります。
条件式を代入して、与式を変形します。
問の解答例 1⃣
\begin{align*}
&\quad x^{\scriptsize{3}} +y^{\scriptsize{3}} = (x+y)^{\scriptsize{3}}-3xy(x+y) \\[ 7pt ]
&\text{であるので、与式は}
\end{align*}
\begin{align*}
\underline{x^{\scriptsize{3}} +y^{\scriptsize{3}}} +z^{\scriptsize{3}} -3xyz &= \underline{(x+y)^{\scriptsize{3}}-3xy(x+y)} +z^{\scriptsize{3}} -3xyz \\[ 7pt ]
&= \underline{(x+y)^{\scriptsize{3}} +z^{\scriptsize{3}}}-3xy \left\{(x+y) +z \right\}
\end{align*}
与えられた条件式と一致する箇所を置き換えることができました。しかし、代入後の式を見ると、まだ3次の項(下線部)が2つ残っています。
条件式との対応関係は以下のようになります。
対応関係を考える
\begin{align*}
a^{\scriptsize{3}} &+b^{\scriptsize{3}} = (a + b)(a^{\scriptsize{2}} -ab +b^{\scriptsize{2}} \ ) \\[ 7pt ]
(x+y)^{\scriptsize{3}} &+z^{\scriptsize{3}}
\end{align*}
\begin{align*}
&\text{$2$ つの式を比べると} \\[ 5pt ]
&\quad a=x+y \\[ 7pt ]
&\quad b=z \\[ 7pt ]
&\text{の対応関係}
\end{align*}
対応関係が分かれば利用できますが、項の数が増えてしまうので、あまり良い方針とは言えません。他の候補を考えると、3次式の因数分解の公式を利用できそうです。
多項式でもカッコでくくれば、1つの文字として扱える。多項式を1つの文字と同じように扱えると、計算力が格段に上がる。
条件式ではなく、3次式の因数分解の公式を利用します。3次の項だけに公式を当てはめて因数分解します。
問の解答例 2⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&= \underline{(x+y)^{\scriptsize{3}} +z^{\scriptsize{3}}}-3xy \left\{(x+y) +z \right\} \\[ 7pt ]
&= \underline{\left\{(x+y)+z \right\} \left\{(x+y)^{\scriptsize{2}} -(x+y) \cdot z +z^{\scriptsize{2}} \right\}}-3xy(x+y+z) \\[ 7pt ]
&= \underline{(x+y+z)} \left\{(x+y)^{\scriptsize{2}} -(x+y)z +z^{\scriptsize{2}} \right\}-3xy \underline{(x+y+z)}
\end{align*}
これで項が2つになりました。各項に共通因数(x+y+z)ができたので、それをくくり出し、残りを整理します。
問の解答例 3⃣
\begin{align*}
&\quad \vdots \\[ 7pt ]
&= \underline{(x+y+z)} \left\{(x+y)^{\scriptsize{2}} -(x+y)z +z^{\scriptsize{2}} \right\}-3xy \underline{(x+y+z)} \\[ 7pt ]
&= (x+y+z) \left\{(x+y)^{\scriptsize{2}} -(x+y)z +z^{\scriptsize{2}}-3xy \right\} \\[ 7pt ]
&= (x+y+z) \left(x^{\scriptsize{2}} +2xy +y^{\scriptsize{2}} -xz -yz +z^{\scriptsize{2}}-3xy \right) \\[ 7pt ]
&= \left(x+y+z \right) \left(x^{\scriptsize{2}} +y^{\scriptsize{2}} +z^{\scriptsize{2}} -xy -yz-zx \right)
\end{align*}
共通因数以外の部分を整理すれば、因数分解の終了です。
因数分解後の式は、記述形式の問題でよく使われます。公式として覚えておくと良いでしょう。
公式として覚えよう
\begin{align*}
&x^{\scriptsize{3}} +y^{\scriptsize{3}} +z^{\scriptsize{3}} -3xyz \\[ 7pt ]
= &\left( x+y+z \right) \left( x^{\scriptsize{2}} +y^{\scriptsize{2}} +z^{\scriptsize{2}} -xy -yz-zx \right)
\end{align*}
少し長くなりますが、記述例は以下のようになります。
問の記述例
\begin{align*}
x^{\scriptsize{3}} +y^{\scriptsize{3}} +z^{\scriptsize{3}} -3xyz &= (x+y)^{\scriptsize{3}}-3xy(x+y) +z^{\scriptsize{3}} -3xyz \\[ 7pt ]
&= (x+y)^{\scriptsize{3}} +z^{\scriptsize{3}}-3xy \left\{(x+y) +z \right\} \\[ 7pt ]
&= \left\{(x+y)+z \right\} \left\{(x+y)^{\scriptsize{2}} -(x+y) \cdot z +z^{\scriptsize{2}} \right\}-3xy(x+y+z) \\[ 7pt ]
&= (x+y+z) \left\{(x+y)^{\scriptsize{2}} -(x+y)z +z^{\scriptsize{2}} \right\}-3xy(x+y+z) \\[ 7pt ]
&= (x+y+z) \left\{(x+y)^{\scriptsize{2}} -(x+y)z +z^{\scriptsize{2}}-3xy \right\} \\[ 7pt ]
&= (x+y+z) \left(x^{\scriptsize{2}} +2xy +y^{\scriptsize{2}} -xz -yz +z^{\scriptsize{2}}-3xy \right) \\[ 7pt ]
&= (x+y+z) \left(x^{\scriptsize{2}} +y^{\scriptsize{2}} +z^{\scriptsize{2}} -xy -yz-zx \right) \\[ 7pt ]
\therefore \ x^{\scriptsize{3}} +y^{\scriptsize{3}} +z^{\scriptsize{3}} -3xyz &= \left( x+y+z \right) \left( x^{\scriptsize{2}} +y^{\scriptsize{2}} +z^{\scriptsize{2}} -xy -yz-zx \right)
\end{align*}
2次式とは言え、項の数が多くなると、因数分解するのが意外と難しくなります。
過去問を解くと分かりますが、センター試験や記述試験では複雑な式を扱うのが当たり前です。たとえば、係数が分数や多項式であるような数式です。
そのような数式と比較すると、与式の因数分解はまだ易しい部類に入ります。そうは言っても扱いづらいのは確かなので、日頃から計算演習をこなして慣れておきましょう。
日頃の演習量で差が付く。数学の基礎力にも関わるので、きちんと積み重ねていこう。
Recommended books
計算力は重要な要素となります。試験では考える時間を多く取るために、いかに計算を手早く行うかが重要です。
計算力の有無は、数学2・Bや数学3では顕著になります。計算に時間がかかりすぎては解けるものも解けません。後悔しないためにも日頃からしっかり鍛えておきましょう。
これから紹介する教材で気になるものがあれば、ぜひ一読してみて下さい。気に入ったら最後まで徹底的にこなしましょう。
大事なことは、自分に合った教材を徹底的に活用することです。どの教材を選ぶにしても、自分の目で中身を確認し、納得してから購入することが大切です。
さいごにもう一度まとめ
- 展開の公式を忘れたときは、パスカルの三角形を利用しよう。
- 二項とも係数が1の多項式の累乗を展開するとき、パスカルの三角形を利用できる。
- パスカルの三角形は、数列でも扱われるので覚えておこう。













