図形の性質|空間における直線と平面について

空間における直線や平面を扱った問題を解いてみよう
次の問題を解いてみましょう。
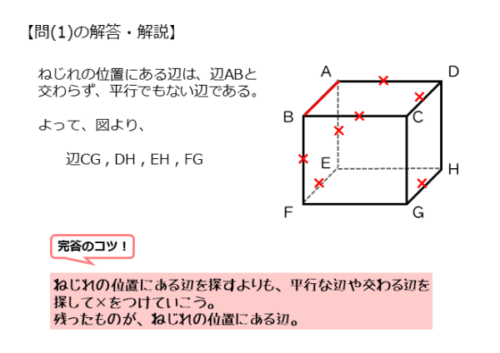
問(1)の解答・解説
問(1)
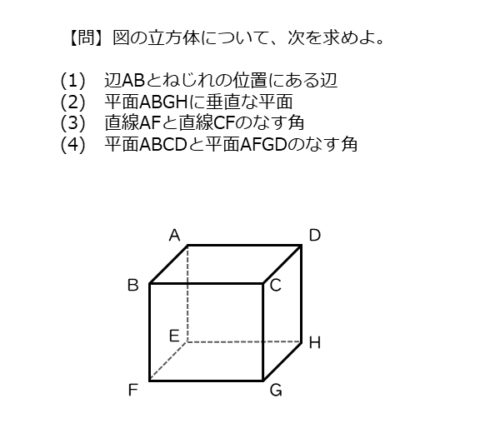
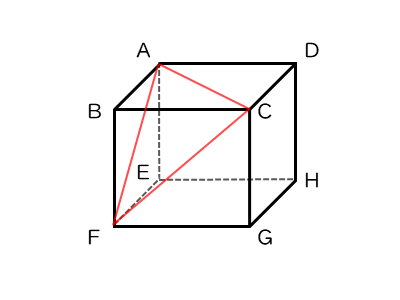
図の立方体 $ABCD-EFGH$ について、次を求めよ。
辺 $AB$ とねじれの位置にある辺
問(1)は、辺ABとねじれの位置にある辺を求める問題です。入試でも頻出の問題です。
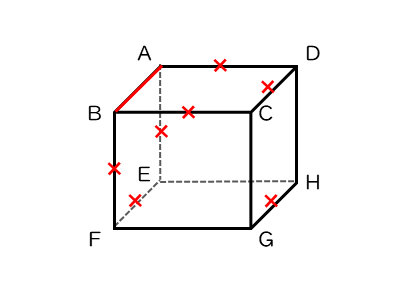
2直線が交わらず、平行でもないとき、ねじれの位置にありますが、辺ABに交わらず、平行でもない辺を探すのは少し面倒です。
こんなときは、辺ABに交わる辺や平行な辺を探して除外します。
問(1)のポイントと解答例をまとめると以下のようになります。
ねじれの位置は、交わる辺と平行な辺を除外する。
問(2)の解答・解説
問(2)
図の立方体 $ABCD-EFGH$ について、次を求めよ。
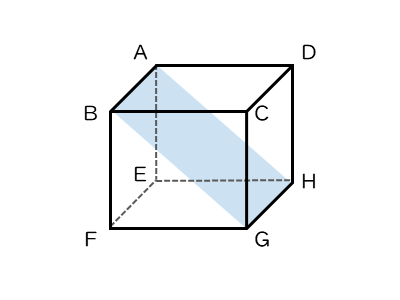
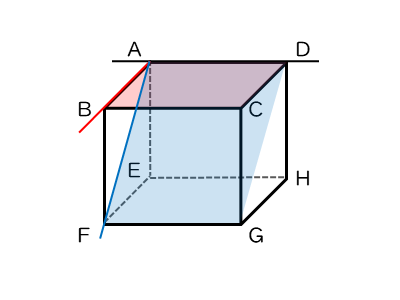
平面 $ABGH$ に垂直な平面
問(2)は、平面ABGHに垂直な平面を求める問題です。2平面が垂直になるときを考えますが、結局のところ、2直線のなす角が直角かどうかを考えなければなりません。
そのためにも、まずは立方体の辺に注目して探します。立方体の辺には、直角の関係になっているものがあります。それを利用します。
辺ABは平面ABGHに含まれる辺で、立方体の一辺です。この辺ABと垂直な辺はBF,BC,AE,ADの4つあります。
2辺BF,BCは平面BFGCに含まれる辺です。また、2辺AE,ADは平面AEHDに含まれる辺です。
これらから、辺ABは2つの平面BFGC,AEHDに垂直であることが分かります。
辺ABは平面ABGHに含まれる辺なので、平面ABGHも2つの平面BFGC,AEHDに垂直となります。
もちろん、交線を使って考えた場合でも、平面ABGHは2つの平面BFGC,AEHDに垂直になっています。
平面上の2直線と直線ℓが垂直 ⇒ 平面⊥直線ℓ ⇒ 平面⊥直線ℓを含む平面
これで終わりではありません。立方体の底面や側面の中で、平面ABGHと垂直なものは他には見られないので、それ以外から探します。
底面や側面以外の面は、平面ABGHと平面CDEFだけです。この2平面が垂直かどうかを調べます。
AHとDEの交点をM、BGとCFの交点をNとすると、2平面の交線は交線MNです。この交線MNに垂直であり、2平面ABGH,CDEFにそれぞれ含まれる直線または線分を探します。ここでは、AMとDMに注目します。
AMとDMは、ともに平面AEHDに含まれます。ですから、交線MNが平面AEHDに垂直であれば、交線MNは、AMとDMにそれぞれ垂直であると言えます。
ここで、AB⊥平面AEHDを参考にします。
ABとMNは平面ABGHに含まれます。ここで、平面ABGHは長方形です。
また、点Mは正方形の対角線である辺AHの中点で、点Nは正方形の対角線である辺BGの中点です。
このような2点M,Nを通るのが交線MNなので、AB//MNとなります。
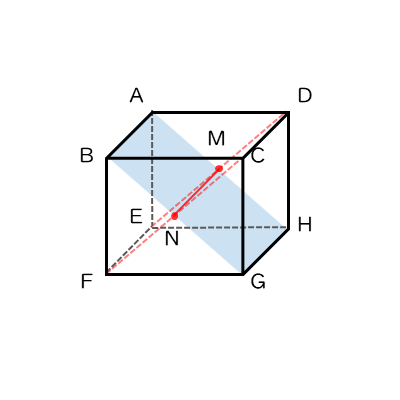
AB//MNであり、AB⊥平面AEHDであることから、MN⊥平面AEHDです。AM,DMは、平面AEHDに含まれので、交線MNに垂直です。これより、直線AMと直線DMのなす角が2平面のなす角になります。
直線AMと直線DMのなす角は、正方形の対角線の性質からAM⊥DMとなるので直角です。これより、平面ABGHは、平面CDEFに垂直であると言えます。
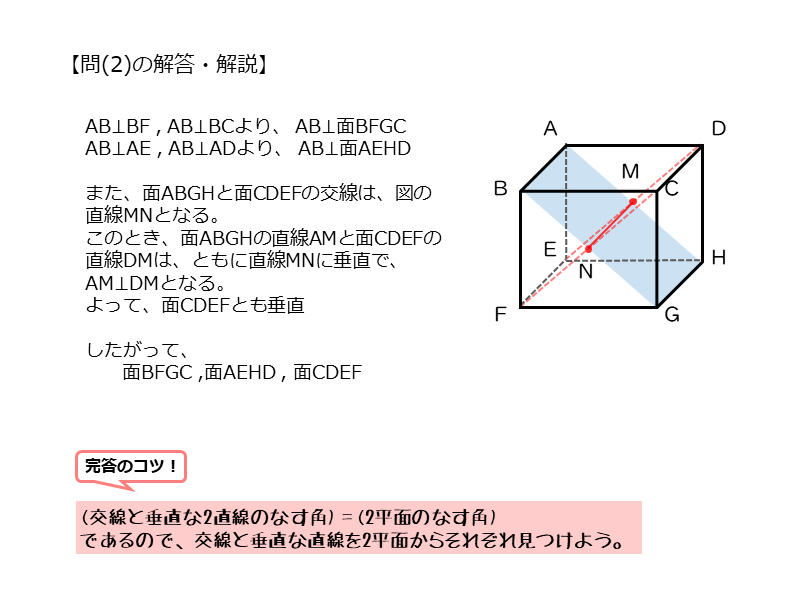
問(2)のポイントと解答例をまとめると以下のようになります。
問(3)の解答・解説
問(3)
図の立方体 $ABCD-EFGH$ について、次を求めよ。
直線 $AF$ と直線 $CF$ のなす角
問(3)は、2直線のなす角を求める問題です。線分AF,CFは立方体の辺ではないので、線分AF,CFを含む平面を抜き出して考えます。
線分AF,CFを含む平面には、たとえば、△ACFがあります。
△ACFの3辺は、すべて立方体の面の対角線になっています。ですから、△ACFはAC=CF=FAの正三角形であることが分かります。
これより、直線AFと直線CFのなす角を求めることができます。
このように、未知の三角形を扱う場合、まず3辺の長さを求めてみましょう。ほとんどの場合が二等辺三角形や正三角形などの特別な三角形になっています。
問(3)のポイントと解答例をまとめると以下のようになります。
未知の三角形では、まず3辺の長さを調べよう。また、空間図形では、角の大きさを見た目で判断しないこと。図形を抜き出す習慣をつけると、ケアレスミスを減らせる。
問(4)の解答・解説
問(4)
図の立方体 $ABCD-EFGH$ について、次を求めよ。
平面 $ABCD$ と平面 $AFGD$ のなす角
問(4)は、2平面のなす角を求める問題です。2平面の交線を探します。2平面の交線は直線ADになります。
各平面上にあり、直線ADと垂直な直線はAB,AFです。この2直線AB,AFのなす角が2平面ABCD,AFGDのなす角です。
2直線AB,AFのなす角は、平面ABFEを抜き出すと簡単に分かります。
平面ABFEにおいて、ABは正方形の一辺で、AFは正方形の対角線です。このことから、2直線AB,AFのなす角を求めることができます。
問(4)のポイントと解答例をまとめると以下のようになります。
2平面のなす角は、交線と垂直な2直線を探す。
空間図形の問題でよく間違うのは、問(2)や問(4)のような問題です。
直線と平面の関係や平面どうしの関係を考えるとき、参考にする直線や線分を見つける必要があり、いくらか訓練が必要です。
そうは言っても、演習をこなすにつれて少しずつコツを掴めるはずです。コツを掴めるまでは辛抱強く演習をこなしましょう。
Recommended books
空間図形を苦手にしている人は意外と多いです。実物を見たり、触ったりする機会が少なく、空間図形に対するイメージがないのが大きな原因かもしれませんが、図形の扱い方を知らないこともその1つかもしれません。
オススメその1-『楽しく学ぶ数学の基礎ー図形分野ー<上:基礎体力編> 』
』
図形を上手に定義する方法から、平面図形や立体図形の種類や理解の仕方までを分かりやすく、面白く解説していきます。本書がきっかけで、図形のおもしろさや奥深さに気づくかもしれません。
オススメその2-『楽しく学ぶ数学の基礎ー図形分野ー<下:体力増強編> 』
』
『楽しく学ぶ数学の基礎ー図形分野ー<上:基礎体力編>』で基礎体力を付けたら、次は下巻で体力を増強しましょう。
さいごに、もう一度、頭の中を整理しよう
- 空間において、直線や平面の関係は大きく分けて3種類。
- 2直線の位置関係では2直線のなす角とねじれの位置に注意しよう。
- 直線と平面の位置関係では、直線が平面に直交するときの条件に注意しよう。
- 2平面の位置関係では、2平面のなす角に注意しよう。