図形の性質|空間における直線と平面について

今回は空間における直線と平面について学習しましょう。
この単元も単独で出題されることが少なく、面積や体積などに派生した問題の導入部分でよく出題されます。もちろん、ここで学習する事柄は、面積や体積を求めるときに必要な知識です。
空間における図形の関係を把握することは、意外と難しいと思います。実際、苦手にしている人は多いようです。空間ベクトルを苦手にしている人は、この単元に戻って復習してみると良いかもしれません。
なお、記事の画像が見辛いときはクリックすると拡大できます。
空間における直線や平面の関係
空間図形を扱った問題では、直線や平面の位置やその関係を把握できないと上手に問題を解くことはできません。直線や平面の位置関係を考えるとき、何と何の関係かで変わってきます。
直線や平面の位置関係
- 2直線の位置関係
- 直線と平面の位置関係
- 2平面の位置関係
それぞれの位置関係において、特に垂直や平行となる条件をしっかり覚えましょう。
2直線の位置関係
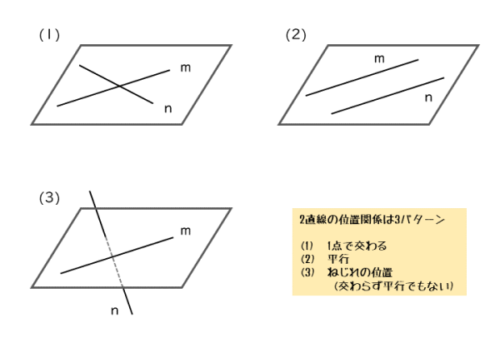
空間に2本の直線があるとき、これらの位置関係は3つに分類されます。言い換えると、2直線の位置関係は3つしかないということです。
2直線の位置関係
- 1点で交わる
- 平行
- ねじれの位置
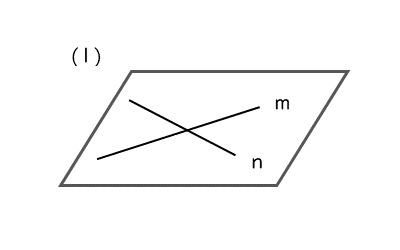
2直線が1点で交わるとき
2直線が1点で交わるのは平面図形でも扱っているので、問題ないかと思います。
2直線が1点で交わるので、2直線は共有点を1つもちます(図(1))。
2直線が1点で交わるとき、角ができます。この角のことを2直線のなす角と言います。
2直線のなす角と言う場合、一般に、鋭角を指します。なお、2直線m,nのなす角が直角のとき、m⊥nと表します。
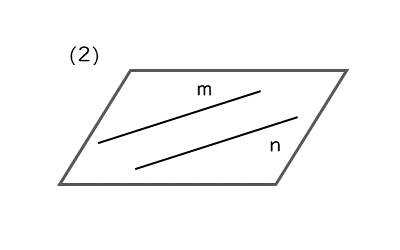
2直線が平行であるとき
2直線が平行であるときも平面図形で扱っています。
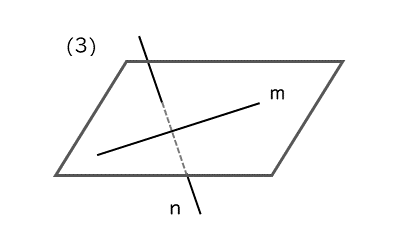
2直線がねじれの位置にあるとき
空間図形において独特の位置関係がねじれの位置です(図(3))。
2直線が交わらず、平行でもないときの位置関係です。このときも2直線は共有点をもちません。
2直線の位置関係について、最も出題されるのがねじれの位置を扱った問題です。
単純な立体であれば問題ないですが、複雑な多面体を扱うときは注意しましょう。
2直線の位置関係について整理すると以下のようになります。
2直線の位置関係は3パターン
- 1点で交わる…2直線のなす角・2直線が直角になるための条件
- 平行…共有点なし
- ねじれの位置…共有点なし
直線と平面の位置関係
空間において直線と平面があるとき、これらの位置関係は3つに分類されます。
直線と平面の位置関係
- 1点で交わる
- 平行
- 直線が平面に含まれる
直線と平面が1点で交わるとき
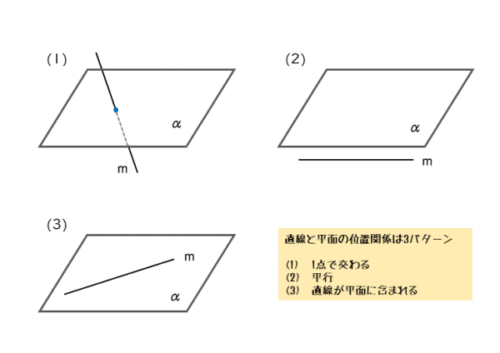
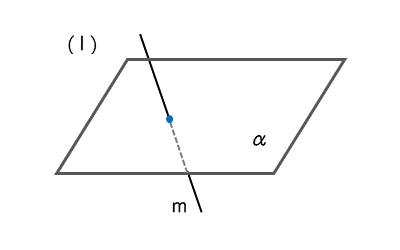
直線と平面が1点で交わるとき、直線と平面は共有点を1つもちます(図(1))。
また、直線と平面が1点で交わるとき、直線mが平面αのすべての直線と垂直であれば、直線は平面に垂直である、または直交すると言い、m⊥αと表します。
平面のすべての直線と垂直であると言っていますが、平面上の少なくとも2つの直線と垂直であることを示せば問題ありません。
直線と平面が平行であるとき
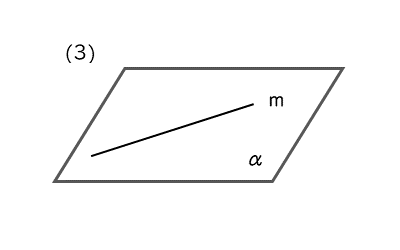
直線が平面に含まれるとき
直線と平面の位置関係を整理すると以下のようになります。
直線と平面の位置関係は3パターン
- 1点で交わる…直線と平面が垂直になるための条件
- 平行…共有点なし
- 直線が平面に含まれる…共有点は直線上のすべての点
2平面の位置関係
空間において2つの平面があるとき、これらの位置関係は2つに分類されます。
2平面の位置関係
- 交わる
- 平行
2平面が交わるとき
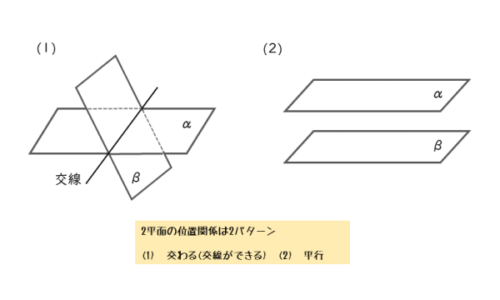
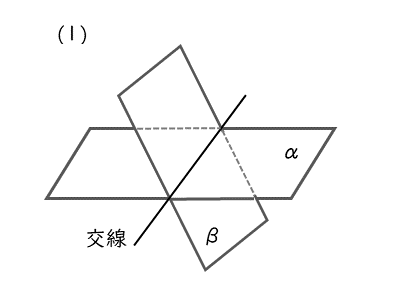
2平面が交わるとき、交線という直線ができます(図(1))。
もし、2平面が有限に広がる平面であれば、交線は線分です。
このとき、2平面が共有するのは、点と言うよりも直線や線分になります。
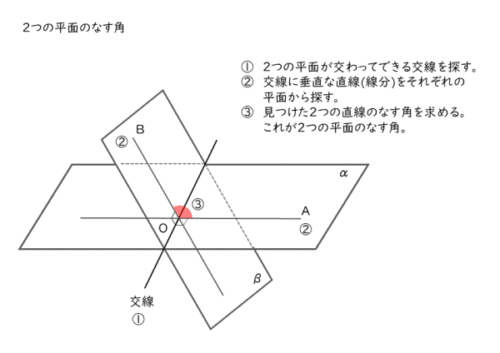
2平面が交わるとき、よく出題されるのが2平面のなす角です。2平面のなす角は、各平面上に、交線に垂直な直線を引いたときの角のことです。
図で言えば、∠AOBが2平面のなす角です。直線OAは平面α上にあり、直線OBは平面β上にあります。
2直線OA,OBはそれぞれ交線に垂直なので、これらのなす角が2平面α,βのなす角になります。
特に、2直線のなす角が直角であれば、2平面のなす角も直角となり、α⊥βと表します。
何となくで角の大きさを求めるのはなく、交線や交線に垂直な2直線を探したり、引いたりしてから、2平面のなす角を求めましょう。
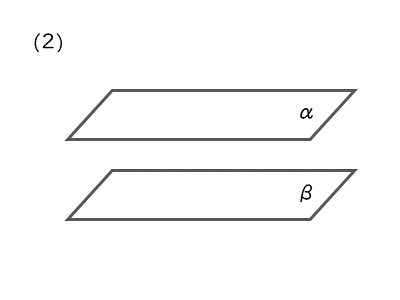
2平面が平行であるとき
2平面の位置関係を整理すると以下のようになります。
2平面の位置関係は2パターン
- 交わる…交線をもつ。2平面のなす角・2平面が垂直になるための条件
- 平行…共有する直線や線分なし
直線や平面の関係をまとめると以下のようになります。
次は、空間における直線や平面を扱った問題を実際に解いてみましょう。