図形の性質|作図について

作図を扱った問題を解いてみよう
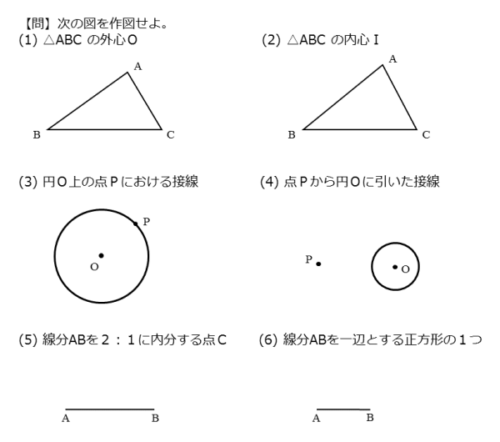
次の問題を解いてみましょう。
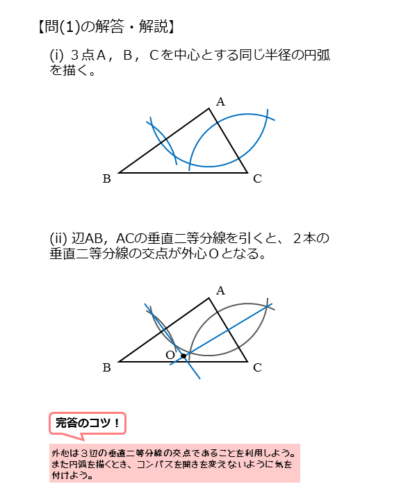
問(1)の解答・解説
問(1)
$\triangle {ABC}$ の外心 $O$ を作図せよ。
問(1)は、三角形の外心を作図する問題です。外心は3辺の垂直二等分線の交点です。垂直二等分線を少なくとも2本引いて交点をつくります。
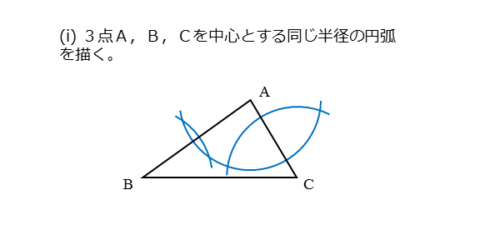
外心の作図(i)
まず、コンパスを使って、3つの頂点A,B,Cを中心とする円(弧)を描きます。どの円(弧)も同じ半径です。
3つの円(弧)が交わって交点ができます。
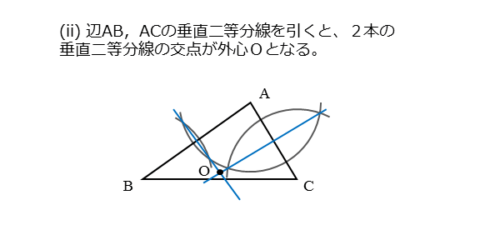
外心の作図(ii)
先ほどできた交点を通る直線を定規で引きます。
A,Bを中心とする円(弧)の交点を通る直線が、線分ABの垂直二等分線です。
また、A,Cを中心とする円(弧)の交点を通る直線が、線分ACの垂直二等分線です。そして、2本の垂直二等分線の交点が△ABCの外心Oです。
作図のときに注意したいのは、作図の跡を残しておくことです。ただ、作図の跡を残しておくので、たくさんの弧や線が入り混じっていると分かり辛くなります。できるだけ簡潔にし、どのように作図したかが分かるようにしておきましょう。
作図の手順一覧は以下のようになります。
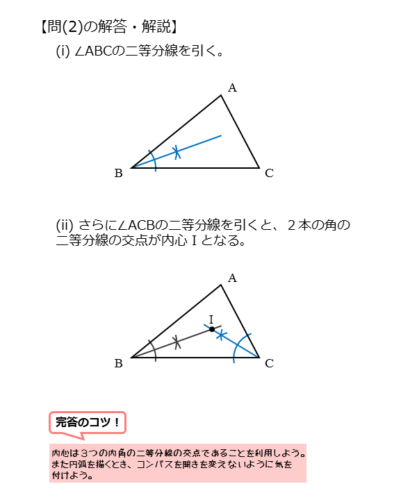
問(2)の解答・解説
問(2)
$\triangle {ABC}$ の内心 $I$ を作図せよ。
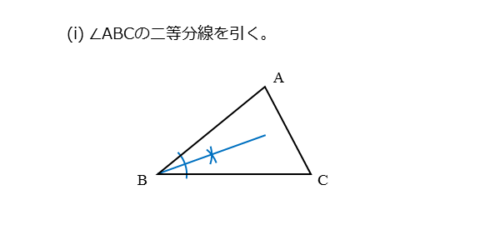
問(2)は、三角形の内心を作図する問題です。内心は3つの内角の二等分線の交点です。内角の二等分線を少なくとも2本引いて交点をつくります。
内心の作図(i)
まず∠ABCの二等分線を引きます。
内心の作図(ii)
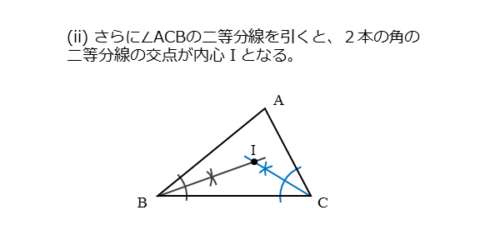
同じ要領で、∠ACBの二等分線を引きます。
2本の角の二等分線が交わって交点ができます。この交点が△ABCの内心Iです。
作図の手順一覧は以下のようになります。
問(3)の解答・解説
問(3)
円 $O$ 上の点 $P$ における接線を作図せよ。
問(3)は、円周上の点における接線を作図する問題です。円の中心と接点とを通る直線が、接線と直交することを利用します。
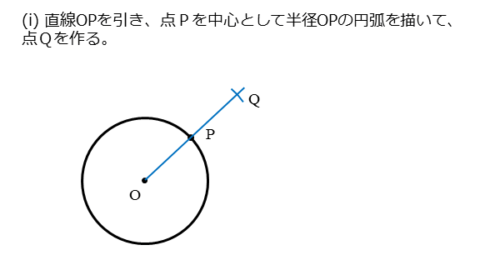
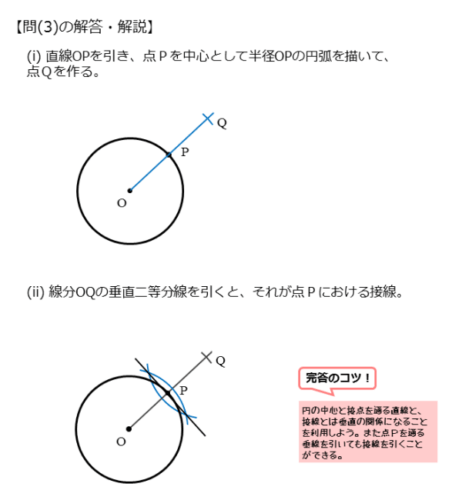
円O上の点Pにおける接線の作図(i)
直線OPを引きます。点Pを中心とする半径OPの円(弧)を描きます。直線OP上には、点Pに関して、点Oと反対側に交点ができます。この交点をQとします。このとき、OP=PQです。
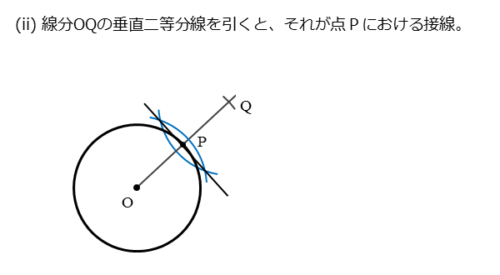
円O上の点Pにおける接線の作図(ii)
次に、コンパスの開きを少し大きくして、点O,Qをそれぞれ中心とする円(弧)を描きます。2つの円(弧)が交わって交点ができます。
さいごに、交点を通る直線を定規で引くと、線分OQの垂直二等分線ができます。この垂直二等分線が円O上の点Pを通る接線です。
作図の手順一覧は以下のようになります。
問(4)の解答・解説
問(4)
点 $P$ から円 $O$ に引いた接線を作図せよ。
問(4)は、円外の点から円に引いた接線を作図する問題です。問(3)では円周上の点であったのに対して、問(4)では円外の点であることに注意しましょう。
作図のイメージは以下のようになります。図のように、円O上にある接点R,Sが分かれば、問(3)のように作図できますが、実際には分かっていません。ですから、接点R,Sをどのようにしてつくるかを考えます。
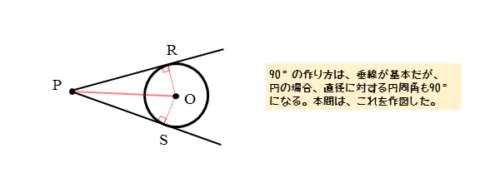
接点R,Sは、直線OR,OSと接線PR,PSとが直交するときの交点です。
90°の角ができることを考慮すると、線分OPを直径とする円の周上にあることが分かります。直径OPに対する円周角がつねに 90°になるからです。
このような直径OPの円上にあって、円O上にもある点が接点R,Sです。つまり、接点R,Sをつくるには、線分OPが直径となる円を描けばよいことが分かります。
点Pから円Oに引いた接線の作図(i)
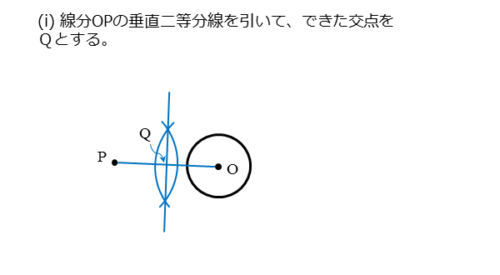
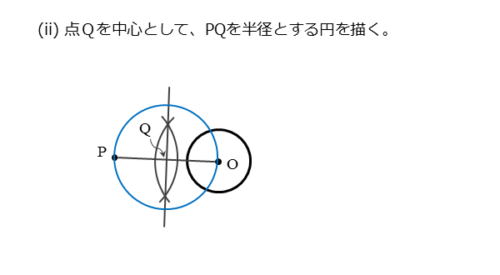
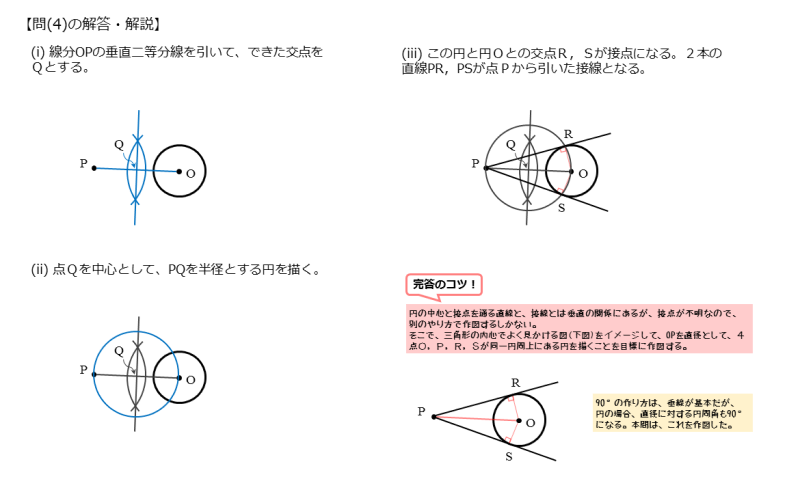
方針が決まったので作図していきます。まず、線分OPの垂直二等分線を引きます。
線分OPとその垂直二等分線が交わって交点ができるので、これをQとします。この点Qが、線分OPを直径とする円の中心です。
点Pから円Oに引いた接線の作図(ii)
次は、点Qを中心とする半径PQ(またはOQ)の円を描きます。
円を描くと、円Oと交わって交点が2つできます。
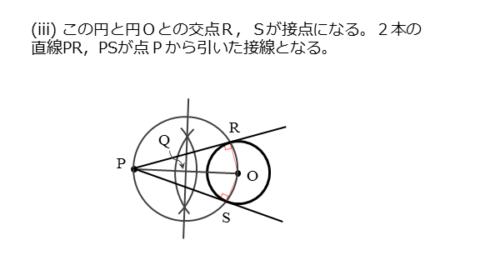
点Pから円Oに引いた接線の作図(iii)
円Oとの交点をそれぞれR,Sとします。この交点R,Sが接点です。これまでが接点の作図手順です。
さいごに、点Pと接点R,Sを通る直線を定規で引きます。この直線PR,PSが、点Pから円Oに引いた接線です。
直角と言われると、垂線を引きたくなりますが、直径に対する円周角でも90°の角をつくることができます。
作図の手順一覧は以下のようになります。
問(5)の解答・解説
問(5)
線分 $AB$ を $2:1$ に内分する点 $C$ を作図せよ。
問(5)は、内分点をつくる問題です。これをマスターすると、外分点も作図できるようになります。
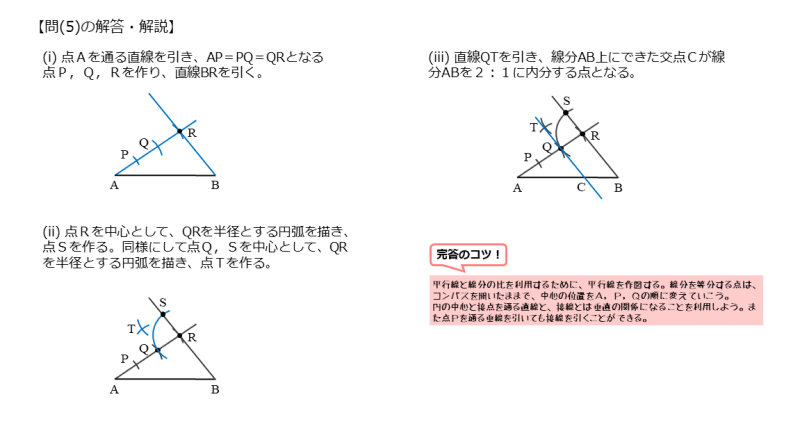
線分ABを2:1に内分する点Cの作図(i)
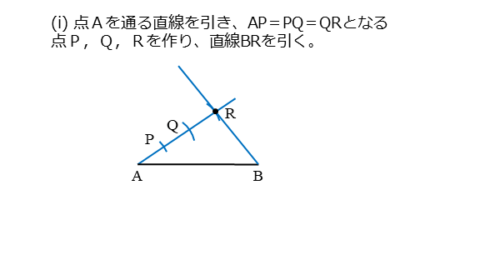
まず、点Aを通る直線を引きます。このとき、線分ABとのなす角が鋭角になるように直線を引きましょう。
自分で引いた直線上に、AP=PQ=QRとなる点P,Q,Rを作ります。
コンパスの開き具合いを変えず、同じ長さとなるように直線上に円(弧)との交点を作ります。これで線分ARを3等分したような図を作図できます。
また、定規を使って、直線BRを引きます。このとき、点R側を少し延長しておくと良いでしょう。
線分を等分するのは、基本作図の「線分を移す」方法で作図する。ただし、コンパスを開きすぎると、点を作りにくくなるので注意しよう。
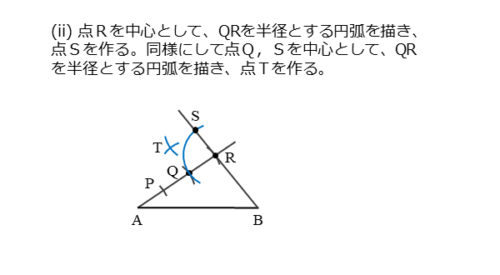
線分ABを2:1に内分する点Cの作図(ii)
次に、点Rを中心とする半径QRの円(弧)を描きます。これと直線BRが交わって交点ができます。この交点をSとすると、QR=RSです。コンパスを開いたままにしておきます。
さらに、点Q,Sをそれぞれ中心とする円(弧)を描きます。交点ができるのでTとします。これでQR=RS=QT=STとなるひし形ができます。
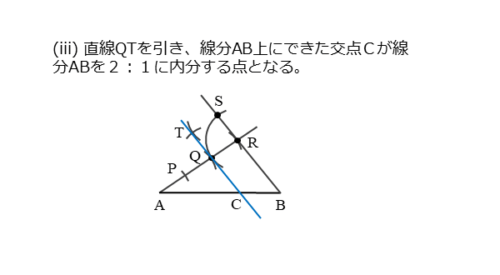
線分ABを2:1に内分する点Cの作図(iii)
さいごに2点Q,Tを通る直線を引きます。
直線QTが線分ABと交わって交点ができます。この点がCです。
直線QTは直線BRに平行です。平行線と線分の比の関係から、AQ:QR=AC:CB=2:1が成り立ちます。このことから、点Cが線分ABを2:1に内分する点となります。
作図の手順一覧は以下のようになります。
問(6)の解答・解説
問(6)
線分 $AB$ を一辺とする正方形を作図せよ。
問(6)は、特定の線分ABを一辺とする正方形を作図する問題です。ひし形の成立条件に、内角の大きさが90°であるという条件が加われば、その図形は正方形になります。
線分ABを一辺とする正方形の作図(i)
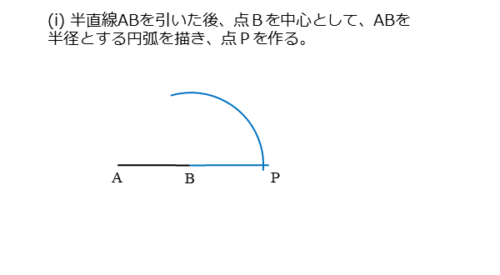
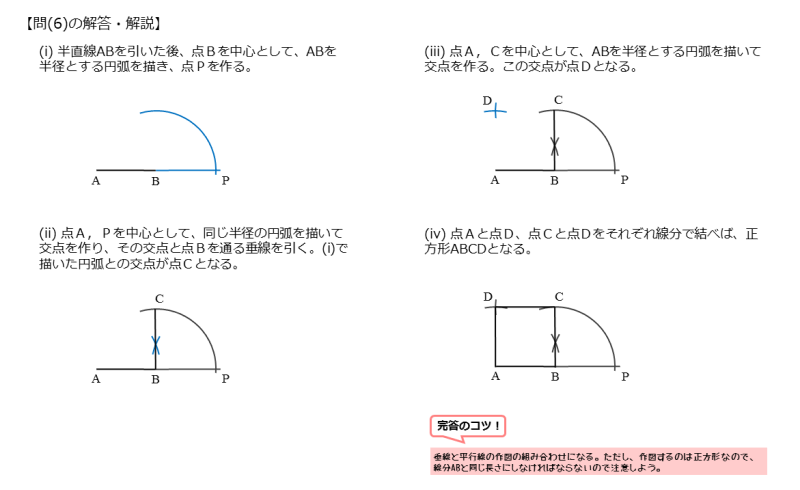
線分ABの一端を延長して、半直線ABにします。延長するのはどちらでも構いません。
線分ABを半直線ABにした後、点Bを中心とする半径ABの円(弧)を描きます。半直線AB上に交点ができるので、これをPとします。このとき、AB=BPです。
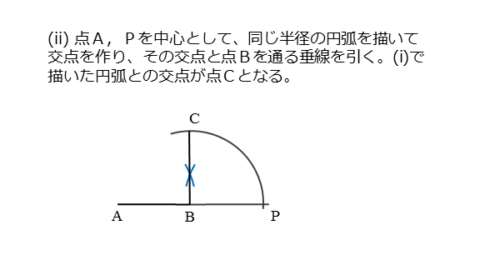
線分ABを一辺とする正方形の作図(ii)
今度はコンパスの開きぐらいを少し大きくして、点A,Pを中心とする円(弧)をそれぞれ描きます。交点ができるので、この交点と点Bを通る直線を定規で引きます。
垂線でも良いのですが、ここでは線分APの垂直二等分線を引いています。垂直二等分線と最初の円(弧)が交わって交点ができます。これを点Cとします。
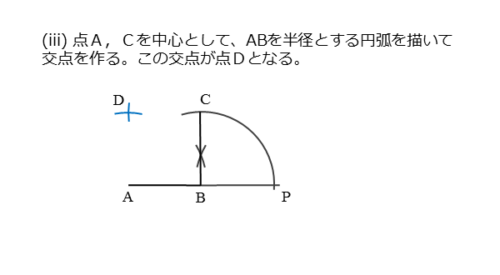
線分ABを一辺とする正方形の作図(iii)
点A,Cをそれぞれ中心とする半径ABの円(弧)を描きます。円(弧)が交わって交点ができます。これを点Dとすると、AB=BC=CD=DAです。
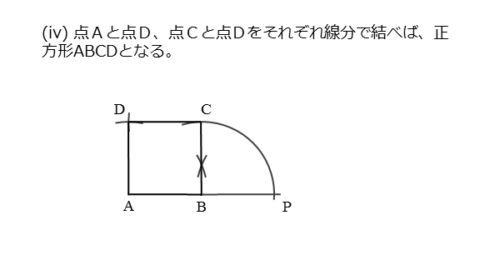
さいごに、定規を使って、点Aと点D、点Cと点Dをそれぞれ結びます。このような手順で線分ABを一辺とする正方形ができます。
点Bを通る垂線を引いたように、点Aを通る垂線を引いても正方形を作図できます。ただ、上述の作図例よりも手間が増えるのであまりお勧めしません。
作図の手順一覧は以下のようになります。
Recommended books
これまで色々な図形を作図しましたが、実際に手を動かしてみることで、図形の性質を上手に利用していることが分かったのではないかと思います。
高校数学ではあまりスポットの当たらない単元ですが、入試問題を解くには作図が必須です。作図なしに図形の問題を解くことは入試レベルではまずできません。
直接の出題はほとんどなくても、図形の問題全般に必ず恩恵を与えることは確かなので、きちんとマスターしておきたい単元です。
オススメその1
図形の作図に特化した教材で、高校生を対象にしたものはほとんど見当たりません。作図できるようになるには、図形に関する知識が必要です。
紹介する『数学パズル 図形編 図形のセンスが自然と身につく!』や『ニュートン式 超図解 最強に面白い!! 数学 図形編』『数学の世界 図形編 増補第2版 奥深き「カタチ」をめぐる数学』は、参考書や問題集と言うよりも、息抜きの読み物ぐらいに捉えると良いでしょう。
三角形に四角形、円や球など、私たちの身のまわりには様々な形のものがあります。それぞれの形にはどのような特徴があるのか。ものがその形になっているのはどうしてか。そんな疑問が解決する「形」の入門書としておすすめの一冊です。
本書は、さまざまな形や、形にまつわる数について、“最強に"面白く紹介する1冊です。本書を読み進めていけば、身のまわりの形について、どんどん興味がわくことでしょう。ぜひご一読ください!
本書は、大好評を博した別冊『数学の世界 図形編』の改訂版です。エッシャーのだまし絵、東京五輪のエンブレム、そして現代社会に役立つ幾何学のテーマが加わりました。ぜひご覧ください!
オススメその2
高校では記述する力がないと問題を解くのも一苦労です。一足飛びに答えが出てくるような問題が少ないので、過程を書き残していく必要があるからです。
そうは言っても答案の書き方に特化した教材はなかなか見当たらないので、模範解答を参考にしながら記述の仕方を身に付けていくのが一般的ではないかと思います。
ここで紹介する『総合的研究 記述式答案の書き方』シリーズは、答案の書き方を身に付けることができる教材です。数学の答案では一般的に因果関係を示しながら記述していきます。これは模範解答を読めば明らかです。
学習の際に「書く」ことを疎かにしなければ、因果関係を意識しながら学習する習慣が徐々に身に付いていきます。因果関係を理解できることは、教科書や参考書を読むときはもちろん、試験では読解問題などに大いに役立ちます。
このように記述する能力は高校の学習において意外と大切な能力ですが、時間を掛けて身に付けていくものです。ですから、やみくもにやっていては時間の浪費になってしまいます。
その助けになるのが『総合的研究 記述式答案の書き方』シリーズではないかと思います。他とはちょっと違ったアプローチで作成されているので、手を出しにくいかもしれませんが、個人的にはおすすめの教材です。
さいごに、もう一度、頭の中を整理しよう
- 7つの基本作図を描けるようになろう。
- 線分の垂直二等分線と角の二等分線については、その性質も含めて重要。
- 作図では基本的にひし形を描くことを考えよう。
- 直角の作図は、垂線だけでなく、直径に対する円周角でも可能。